简述 Erasure Code，EC 纠删码原理

你知道的越多，不知道的就越多，业余的像一棵小草！

你来，我们一起精进！你不来，我和你的竞争对手一起精进！

编辑：业余草

blog.csdn.net/shelldon

推荐：https://www.xttblog.com/?p=5165

本文只对 BAT 大厂使用过【纠删码】的开发人员有用，以及对算法感兴趣，课题研究等人员有用。其他人员以及不对纠删码感兴趣的建议忽略本文！

什么是Erasure Code

Erasure Code（简称 EC），即纠删码，是一种前向错误纠正技术（Forward Error Correction，FEC），主要应用在网络传输中避免包的丢失，存储系统利用它来提高存储、可靠性。相比多副本复制而言，纠删码能够以更小的数据冗余度获得更高数据可靠性，但编码方式较复杂，需要大量计算。纠删码只能容忍数据丢失，无法容忍数据篡改，纠删码正是得名与此。

EC 的定义：Erasure Code 是一种编码技术，它可以将 n 份原始数据，增加 m 份数据，并能通过 n+m 份中的任意 n 份数据，还原为原始数据。即如果有任意小于等于 m 份的数据失效，仍然能通过剩下的数据还原出来。

目前，纠删码技术在分布式存储系统中的应用主要有三类，阵列纠删码（Array Code: RAID5、RAID6等）、RS(Reed-Solomon)里德-所罗门类纠删码和 LDPC(LowDensity Parity Check Code)低密度奇偶校验纠删码。

RAID 是 EC 的特殊情况。在传统的 RAID 中，仅支持有限的磁盘失效，RAID5 只支持一个盘失效，RAID6 支持两个盘失效，而 EC 支持多个盘失效。

EC 主要运用于存储和数字编码领域。例如磁盘阵列存储（RAID 5、RAID 6），云存储（RS）等。

LDPC 码也可以提供很好的保障可靠性的冗余机制。与 RS 编码相比，LDPC 编码效率要略低，但编码和解码性能要优于 RS 码以及其他的纠删码，主要得益于编解码采用的相对较少并且简单的异或操作。LDPC 码目前主要用于通信、视频和音频编码等领域。

本文主要讲解 RS 类纠删码。

Reed-Solomon Code

RS code是基于有限域的一种编码算法，有限域又称为Galois Field，是以法国著名数学家伽罗华（Galois）命名的，在RS code中使用GF(2^w)，其中2^w >= n + m。

RS code 的编解码定义如下：

❝

编码：给定 n 个数据块（Data block）D1、D2……Dn，和一个正整数 m，RS 根据 n 个数据块生成 m 个编码块（Code block），C1、C2……Cm。

❞

解码：对于任意的 n 和 m，从 n 个原始数据块和 m 个编码块中任取 n 块就能解码出原始数据，即 RS 最多容忍 m 个数据块或者编码块同时丢失。

RS 编解码中涉及到矩阵求逆，采用高斯消元法，需要进行实数加减乘除四则运算，无法作用于字长为w的二进制数据。为了解决这个问题， RS 采用伽罗华群 GF（2^w）中定义的四则运算法则。

GF(2^w）域有 2^w 个值， 每个值都对应一个低于 w 次的多项式， 这样域上的四则运算就转换为多项式空间的运算。GF(2^w) 域中的加法就是 XOR， 乘法通过查表实现，需要维护两个大小为 2^w -1 的表格: log 表 gflog，反 log 表 gfilog。

乘法公式：

❝

a * b = gfilog(gflog(a) + fglog(b)) % (2^w -1)

❞

RS code编码原理

RS 编码以 word 为编码和解码单位，大的数据块拆分到字长为 w（取值一般为8或者16位）的 word，然后对 word 进行编解码。数据块的编码原理与 word 编码原理相同，后文中一 word 为例说明，变量 Di, Ci 将代表一个 word。

把输入数据视为向量D=(D1，D2，..., Dn）, 编码后数据视为向量（D1, D2,..., Dn, C1, C2,.., Cm)，RS 编码可视为如下图所示矩阵运算。

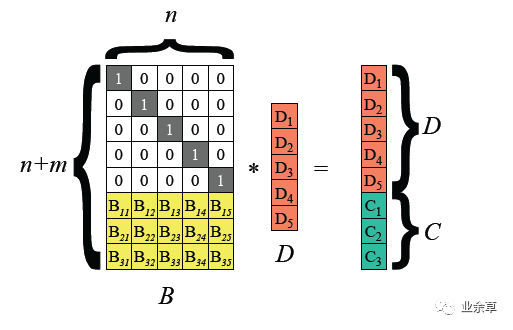
上图最左边是编码矩阵（或称为生成矩阵、分布矩阵，Distribution Matrix），编码矩阵需要满足任意n*n子矩阵可逆。

为方便数据存储，编码矩阵上部是单位阵（n行n列），下部是m行n列矩阵。下部矩阵可以选择范德蒙德矩阵或柯西矩阵。

RS code编码数据恢复原理

RS最多能容忍m个数据块被删除。数据恢复的过程如下：

（1）假设D1、D4、C2丢失，从编码矩阵中删掉丢失的数据块/编码块对应的行。

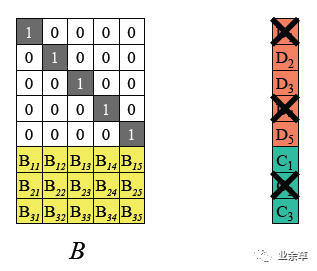
根据图1所示RS编码运算等式，可以得到如下B' 以及等式。

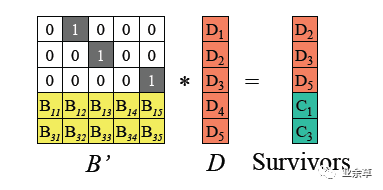
（2）由于B' 是可逆的，记B'的逆矩阵为 (B'^-1)，则B' * (B'^-1) = I 单位矩阵。两边左乘B' 逆矩阵。

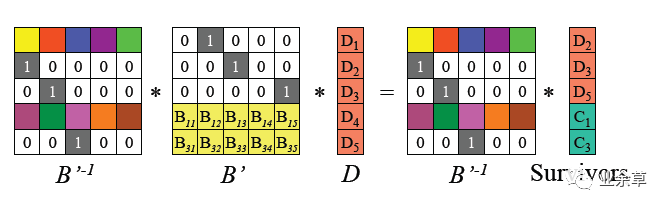
（3）得到如下原始数据D的计算公式

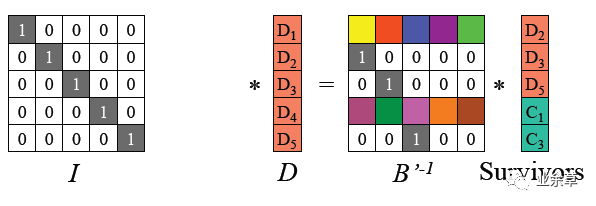
即恢复原始数据D：

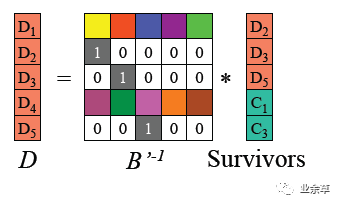
（4）对D重新编码，可得到丢失的编码码

RS code编码的限制

1. 数据恢复代价高和数据更新代价高，因此常常针对只读数据，或者冷数据。

2. RS编码依赖于两张2^w-1大小的log表， 通常只能采用16位或者8位字长，不能充分利用64位服务器的计算能力， 具体实现上可能要做一些优化。

编码矩阵

基于范德蒙德（Vandermonde）矩阵

在线性代数中有一种矩阵称为范德蒙德矩阵，它的任意的子方阵均为可逆方阵。一个m行n列的范德蒙德矩阵定义如下，其中Ai 均不相同，且不为0。

令A1、A2...An分别为1、2、3...n，则得到范德蒙德矩阵为：

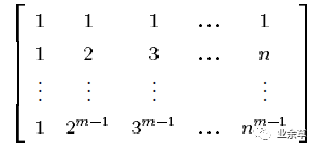
编码矩阵就是单位矩阵和范德蒙德矩阵的组合。输入数据（D）和编码矩阵的乘积就是编码后的数据。

算法复杂度

采用这种方法的算法复杂度还是比较高的，编码复杂度为O（mn），其中m为校验数据个数，n为输入数据个数。解码复杂度为O（n^3）。

基于柯西（ Cauchy）矩阵

柯西矩阵的任意一个子方阵都是奇异矩阵，存在逆矩阵。而且柯西矩阵在迦罗华域上的求逆运算，可以在O（n^2）的运算复杂度内完成。

使用柯西矩阵，比范德蒙德矩阵的优化主要有两点：

1. 降低了矩阵求逆的运算复杂度。范德蒙矩阵求逆运算的复杂度为O（n^3），而柯西矩阵求逆运算的复杂度仅为O（n^2）。

2. 通过有限域转换，将GF（2^w）域中的元素转换成二进制矩阵，将乘法转换为逻辑与，降低了乘法运算复杂度。（二进制的加法即XOR，乘法即AND）

柯西矩阵的描述如下：

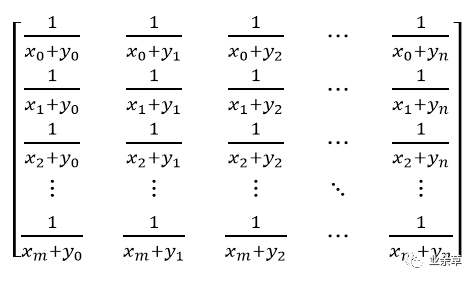
Xi 和Yi 都是迦罗华域GF（2^w）中的元素。

基于柯西矩阵的编码矩阵：

柯西编解码过程优化

在范德蒙编码的时候，我们可以采用对数/反对数表的方法，将乘法运算转换成了加法运算，并且在迦罗华域中，加法运算转换成了XOR运算。

柯西编解码为了降低乘法复杂度，采用了有限域上的元素都可以使用二进制矩阵表示的原理，将乘法运算转换成了迦罗华域“AND运算”和“XOR逻辑运算”，提高了编解码效率。

从数学的角度来看，在迦罗华有限域中，任何一个GF（2^w）域上的元素都可以映射到GF（2）二进制域，并且采用一个二进制矩阵的方式表示GF（2^w）中的元素。

例如，GF（2^3）域中的元素可以表示成GF（2）域中的二进制矩阵：

上图中，黑色方块表示逻辑1，白色方块表示逻辑0。通过这种转换，GF（2^w）域中的阵列就可以转换成GF（2）域中的二进制阵列。生成矩阵的阵列转换表示如下：

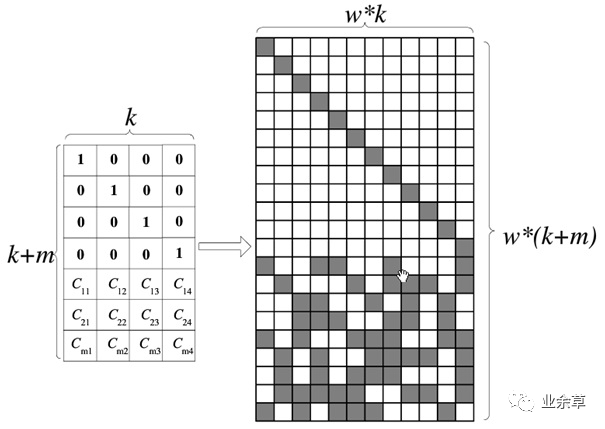
在GF（2^w）域中的编码矩阵为K*（K+m），转换到GF（2）域中，使用二进制矩阵表示，编码矩阵变成了wk* w(k+m)二进制矩阵。

采用域转换的目的是简化GF（2^w）域中的乘法运算。在GF（2）域中，乘法运算变成了逻辑与运算，加法运算变成了XOR运算，可以大大降低运算复杂度。

和范德蒙编解码中提到的对数/反对数方法相比，这种方法不需要构建对数/反对数表，可以支持w为很大的GF域空间。采用这种有限域转换的方法之后，柯西编码运算可以表示如下：

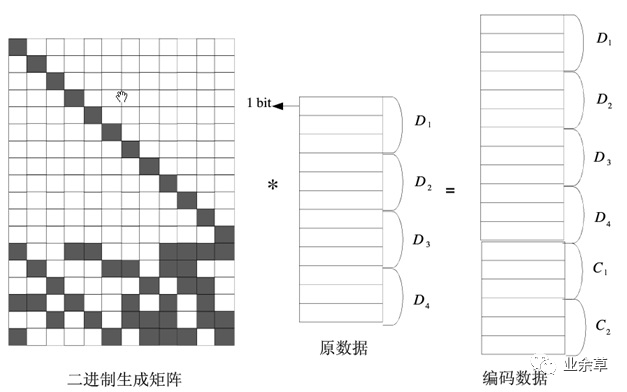
算法复杂度

使用柯西矩阵要优于范德蒙德矩阵的方法，柯西矩阵的运算复杂度为O（n *（n - m）），解码复杂度为O（n^2）。

参数w影响

选择GF（2^w）中的w参数是，需要满足k+n <= 2^w。

对于柯西矩阵的RS编码，还需要满足coding Block size %  ( w * packet ) == 0。（具体参数设置和意义见 Jerasure实现）

关于Erasure Code，有一个开源的实现Jerasure，是由James S. Plank教授开发。还有一个开源项目FECpp，也是关于EC code的。

RS编码升级

RS编码后的数据，如果丢失了一块，恢复丢失的数据需要最少读取n块数据。在生产环境中，硬盘故障经常发生，恢复数据对网络IO和CPU都会有较大的消耗。

因此有些公司在EC编码的基础上做了一些改进，使用LRC或SEC替换RS编码。

LRC - Locally Repairable Code 本地副本存储

LRC编码与RS编码方式基本相同，同时增加了额外的数据块副本。  LRC编码本质上是RS编码+2副本备份。

LRC编码步骤如下：

1. 对原始数据使用RS编码，例如编码为4：2，编码结果为4个数据块：D1、D2、D3、D4，2个编码块C1、C2；

2. 原始数据做2副本，将4个数据块的前2个数据块和后2个数据块，分别生成2个编码块，即R1=D1D2，R2=D3D4；

3. 如果某一个数据块丢失，例如D2丢失，则只需要R1和D1即可恢复D2；

LRC的编码矩阵中增加了步骤b的2副本编码，样子如下：

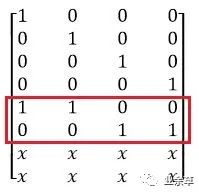
SEC - Sparse Erasure Code 稀疏纠删码

LRC编码中只对数据块做了2副本，当编码块丢失时，仍然需要读取n块数据来重新计算编码块。

SEC编码中对数据块和编码块都做增加了校验块。

SEC编码本质上是RS编码+奇偶校验块。  SEC编码步骤如下：

1. 对原始数据使用RS编码，例如编码为4：2，编码结果为4个数据块：D1、D2、D3、D4，2个编码块C1、C2；

2. 生成D1D2的校验块X1，D3D4的校验块X2，C1C2的校验块X3；

3. 当数据块或编码块中的某一个丢失时，例如C2丢失，通过C1和校验块X3即可恢复C2；

SEC同样通过增加存储块，减少了恢复数据是的网络和CPU开销。

附 FEC 介绍

在信息中按照某种规则加上一定的冗余位，构成一个码字，称为差错控制编码过程。在接收端接收到码字，或从存储设备中读取码字后，查看信息位和冗余位，并检查他们之间的关系是否正确，以确定是否有差错发生，称为校验。

Forward  Error Correction，FEC- 前向纠错编码技术通过在传输码列中加入冗余纠错码，在一定条件下，通过解码可以自动纠正传输误码。这种编码的译码设备较复杂。

除FEC之外，还有两种差错控制编码：Automatic repeat request（ARQ）检错重发（或自动请求重传），Hybrid  Error Correction（HEC）混合纠错。

检错重发由发送端送出能够发现错误的码，接收端如果发现错误，通过反向信道把这一判决结果反馈给发送端。然后，发送端把接收端认为错误的信息再次重发。其特点是需要反馈信道，译码设备简单。

混合纠错是 ARQ和 FEC方式的混合。发送端同时送出具有检错和纠错能力的码，如果接收端收到信码在纠错能力以内，则自动进行纠正。如果超出纠错能力，则经过反馈信道请求发送端重发。