matlab simulink chapter4：控制系统的数学模型

本文参阅《Matlab/Simulink与控制系统仿真》一书，做一些笔记，帮助自己学习。

系统的数学模型 ----> 系统的仿真处理 —> 设计一个合适的控制器，使系统响应到预期效果

线性系统中，常见的线性模型有：
传递函数模型
状态方程模型
零极点增益模型
部分分式模型等

动态过程微分方程描述

微分方程是控制系统模型的基础

动态微分方程描述的是被控制量与给定量或扰动量之间的函数关系，给定量和扰动量可以看成 系统的输入量，被控制量看成输出量。

建立微分方程的时候，一般从系统的环节着手，先确定各环节的输入量和输出量，以确定其工作状态，并建立各环节的微分方程，而后消去中间变量，最后得到系统的动态微分方程

对于比较复杂的系统，建立系统微分方程一般可采用以下步骤：

1. 将系统划分为多个环节，确定各环节的输入和输出信号，每个环节可考虑写一个方程
2. 根据物理定律或通过实验等方法得出的物理规律，列出各环节的原始方程式，并考虑适当简化、线性化
3. 将各环节方程式联立，消去中间变量，最后得出只包含输入变量、输出变量以及参量的系统方程式。

若已知输入量以及变量的初始条件，对微分方程进行求解，就可以得到系统输出量的表达式，并由此对系统进行性能分析。

Matlab 提供了 ode23 、ode45 等微分方程的数值解法函数，不仅适用于线性定常系统，也适用于 非线性和时变系统。

%%
课本 P73 页代码
%%
clear
% 清除工作空间的变量
t0 = 0; tfinal = 10;
% 响应时间
x0 = [0.2; 0];
% 初始化，电感电流为0，电容电压为 0.2V
%%
[t0 tfinal] 求解区间， X0是初始值
[t, x]=ode45('rlcsys', [t0 tfinal], x0);
% rlcsys 是系统微分方程的描述函数
%%
figure(1);
subplot(211); plot(t,x(:,1));
grid;
% 绘制状态响应图并添加栅格
title('电容电压/V');
xlabel('时间/s')
subplot(212);
plot(t,x(:,2));
grid;
% 绘制状态响应图并添加栅格
title('电感电流/A');
xlabel('时间/s')
%%
figure(2);
vc =x(:,1);
i = x(:,2);
plot(vc, i); grid;
title('电感电流与电容电压的关系曲线/A');
xlabel('电容电压/V')
ylabel('电感电流/A')

function xdot = rlcsys(t,x)
Vs = 1.5; R = 1.6; L = 2.1; C=0.30;
xdot = [x(2)/C; 1/L*(Vs - x(1) - R * x(2))];
end

ode45 求解方法

ode45 求解非刚性微分方程 - 中阶方法

[t,y] = ode45(odefun,tspan,y0)

其中 tspan = [t0 tf] 求微分方程组 $y^{\prime }=f(t,y)$ 从 t0 到 tf 的积分，初始条件为 y0。解数组 y 中的每一行都与列向量 t 中返回的值相对应。

其中，关于 ode45 中的 rlcsys 代表了要求解的函数odefun，指向待积分函数的句柄。
对于标量 t 和 列向量 y 来说，函数dydt = odefun(t, y)必须返回数据类型为 single 或者 double 的列向量 dydt，该列向量对应于f(t,y)。odefun 必须同时接受输入产生 t 和 y，即使其他一个参数未在函数中使用也是如此。

对于方程组，odefun 的输出为向量，向量中的每个元素都是一个方程的解，例如

tspan 积分区间，指定为 向量。其中，必须至少是 一个二元素向量[t0 tf]，用于指定初始时间和最终时间。要获取 t0 到 tf 之间的特定时间的解，请使用 [t0, t1, t2, … , tf]形式的长向量。 tspan 中的元素必须单调递增或单调递减。

求解器在初始时间 tspan(1) 施加由y0给出的初始条件，然后求tspan(1) 到tspan(end)的积分：

1. 如果 tspan 由两个元素，[t0 tf]，求解器将返回在该区间内的每个内部积分计算的解。即 由 从 t0 到 tf 之间的每个值得解
2. 如果 tspan 包含两个以上的元素 [t0, t1, t2, … , tf] ，求解器 将返回在给定点处计算的解。但是，求解器不会精确步进到 tspan 中指定的每一个点。此时，求解器使用自己的内部积分来计算解，然后再tspan中请求的各点处计算解
3. 将 tspan 指定为 二元素向量还是包含中间点得向量，求解器获得得解可能有所不同

y0 初始条件，指定为向量。y0 得长度必须与 odefun 得向量输出相同，使y0为odefun中定义得每个方程包含一个初始条件。即，y0向量以及输出向量的长度和要求解的微分方程的个数相同。

输出参数 t: 计算点，以列向量形式返回

1. 如果 tspan 包含两个元素，[t0 tf]，则 t 包含 用于执行积分的内部计算点
2. 如果 tspan 包含两个以上元素，则t与tspan相同

输出参数 y: 解，以数组形式返回，y中的每一行都与 t 的相应行中返回的值处的解相对应。

拉氏变换与控制系统模型

动态系统的数学模型：微分方程、差分方程、传递函数、状态方程等

其中，微分方程描述的系统模型，通过求解微分方程，可以得到系统随时间的变化规律，比较直观；但是当微分方程的阶数较高的时候，求解就回变得十分困难，不易实现，=== 采用 拉氏变换 将原来的时域转换为复频域，进而吧微分方程转换为 代数方程，而代数方程的求解是比较简单的，求解代数方程之后，再通过拉氏变换得到微分方程的解。

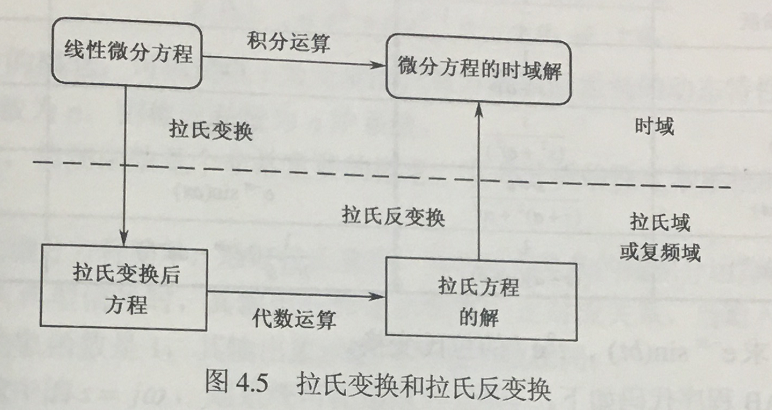
线性微分方程 通过拉氏变换得到代数方程，采用代数运算求解代数方程，得到代数解，再通过拉氏反变换得到微分方程的时域解

时域函数$f(t)$的拉氏变换定义如下：$$F(s)={\int }_0^{\infty }f(t)e^{-st}dt$$
其中，$s$是拉式算子，单位是 1/time， 即频率。下图是 拉氏变换 的基本定理

常见的 拉氏变换表

下面的例子是 求解 $e^{-at}sin(bt)$ 和 $t^2{e}^{-t}$ 的拉氏变换

% 求解拉氏变换
% 函数 laplace 主要求解一个微分方程的 拉氏变换方程
syms t s;
% 定义了符号变量
syms a b positive
% 定义符号变量
D1 = exp(-a * t) * sin(b*t);
D2 = t^2 * exp(-t);
MS1 = laplace(D1, t, s);	% 独立变量为 t，传递变量为 s
MS2 = laplace(D2, t, s);
%% 执行结果输出
% MS1 = b/((a + s)^2 + b^2)
% MS2 = 2/(s + 1)^3

数学模型的描述

为了对系统的性能进行分析的步骤首先要 建立其数学模型

控制系统常见的模型有：
传递函数模型、
零极点形式的数学模型、
状态空间模型

传递函数模型

表达了系统内在的固有特性；不能表明系统的物理特性和物理结构

许多物理性质不同的系统却有着相同的传递函数

其中，线性定常系统的传递函数定义为：在零初始条件下，输出量(响应函数)的拉普拉斯变换与输入量(驱动函数)的拉普拉斯变换之比

1. 零初始条件
2. 输出量是响应函数，输入量是 驱动函数；传递函数为 输出比输入

传递函数中，分母中s的最高次数为 n，则称该系统为n阶系统；传递函数的零极点(零点（分子为0）和极点(分母为0))分布决定系统的动态特性。对于线性定常系统，传递函数中的s的系数均为常数，且$a_0$不等于0，这个时候可以在matlab中使用下面的方式来进行表示：使用 tf函数来表示 传递函数

%% 传递函数表示
num = [1, 2, 3, 4];
den = [7, 8, 9, 10];
% 都是按照s的降次幂来进行排序的
G = tf(num,den);
% 执行效果
s^3 + 2 s^2 + 3 s + 4
G =
------------------------
7 s^3 + 8 s^2 + 9 s + 10
num=[1,10];
den=[1,5,4,3,2];
G=tf(num,den);
% 执行结果：
s + 10
G =
-----------------------------
s^4 + 5 s^3 + 4 s^2 + 3 s + 2

零极点形式的数学模型

是传递函数的另外一个表示形式，原理是 分别对原系统传递函数的分子、分母进行因式分解处理，以获得系统的零点和极点的表示形式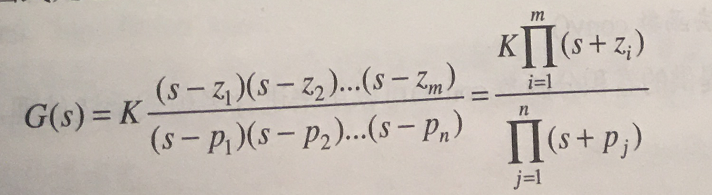
其中，K表示系统增益，$-z_i$为系统的零点，$-p_j$为系统的极点；传递函数的分母多项式就是它的特征多项式，它等于零的方程就是传递函数的特征方程，特征方程的根也是传递函数的极点。

传递函数的极点：决定了所描述系统的自由运动模态
传递函数的零点：影响系统各个模态在系统响应中所占的比重。

控制系统 常用到 并联系统，这时 就要对系统函数进行求解，使其表现为一些基本控制单元的和的形式，也就是用部分分式表示$$G(s)=K_1\frac{s-z_1}{s-p_1}+K_2\frac{s-z_2}{s-p_2}+....+K_n\frac{s-z_n}{s-p_n}=\sum _{i=1}^n{K}_i\frac{s-z_i}{s-p_i}$$式中，$K_i$ 为各个部分分式的增益；$-z_i$ 是分子多项式的根，称为系统的零点；$-p_j$ 是分母多项式的根，称为系统的极点。

状态空间模型

以时域分析为主，着眼于系统的内部状态及其内部联系
状态：系统动态信息的集合，在表征系统信息的所有变量中，能够全部描述系统运行的最小数目的一组对立变量称为 系统的状态变量，其选取不是唯一的
具有n个状态、r个输入和m个输出的线性时不变系统，用矩阵符号表示的状态空间模型如下：
$$\begin{array}{rl}\dot{x}& =Ax+Bu(状态方程)\\ y& =Cx+Du(输出方程)\end{array}$$式中，
状态变量$x$是n维的，
输入向量 u 是 r 维的，
输出向量 y 是 m 维的，

状态矩阵 A 是n * n维的，
输入矩阵B是n * r维的，
输出矩阵C 是m*n 维的，
前馈矩阵 D 是 m * r 维的，

对于时不变系统，A、B、C、D都是常数矩阵。

Matlab / Simulink 在模型中的应用

多项式处理相关的函数

Matlab 中多项式用行向量表示，行向量元素依次为降幂排列的多项式的系数

多项式乘法函数

conv() 进行多项式乘法处理，其常见的函数调用格式为

% A B 为 一个多项式的系数(降幂排列) C 为多项式的乘积多项式，其中 conv 函数允许多级嵌套
C = conv(A, B)

多项式求根函数

p 为多项式，r为所求的根
r = root(p)

由根创建多项式函数

某一个多项式的因式分解式或特征根r，可用函数 ploy 函数直接得出特征多项式系数矢量p

p = poly(r)

求多项式在给定点的值函数

如果已知多项式 p，要求其变量取a时的值v，可用 polyval() 来求取

v = polyval(p, a)

建立传递函数相关的函数

利用传递函数分子和分母多项式的系数向量进行描述，分子 num、分母 den 多项式的系数向量分别为 ：
num = [$b_m,b_{m-1},,b_{m-2}...,b_0$], den = [$1,a_{n-1},a_{n-2}...,a_0$]，分别为按照系数降幂排列

1. 建立传递函数模型的函数 tf()

sys = tf(num, den);
% 常规系统 G(s) 的传递函数
sys = tf(num, den, 'InputDelay', tau);
% 带有时间延迟的系统传递函数 tau 为系统延迟时间的数值

带时间延迟系统的传递函数$G_d(s)=G(s)e^{-\tau s}$

2. 提取模型中分子分母多项式系数的函数 tfdata()

从传递函数中提起模型中的分子分母多项式系数

[num, den] = tfdata(sys, 'v') % v 是关键词，其功能是返回列向量形式的分子分母多项式系数

建立零极点形式的数学模型相关函数

1. 建立零极点形式数学模型的函数 zpk()
2. 提取模型中 零极点 和增益向量的函数zpkdata()
3. 传递函数模型部分分式展开的函数 residue()，是对两个多项式的比进行部分展开，以及把传递函数分解为微分单元的形式

sys = zpk([z], [p]. [k]); % 分别为系统的零极点和增益向量
sys = zpk(z, p, k, 'InputDelay', tau)
[z, p, k] = zpkdata(sys, 'v')
[r, p, k] = residue(b. a);
% 向量b 和向量 a 是按s降幂排列的多项式系数。部分分式展开后，余数返回到向量r，极点返回到列向量p，常数项返回到k

建立状态空间模型相关函数

A B C D 系统状态空间矩阵

1. 建立 ss()
2. 提取 ssdata()

sys = ss(A, B, C, D);
[A, B, C, D] = ssdata(sys);

simulink 中的控制系统模型表示

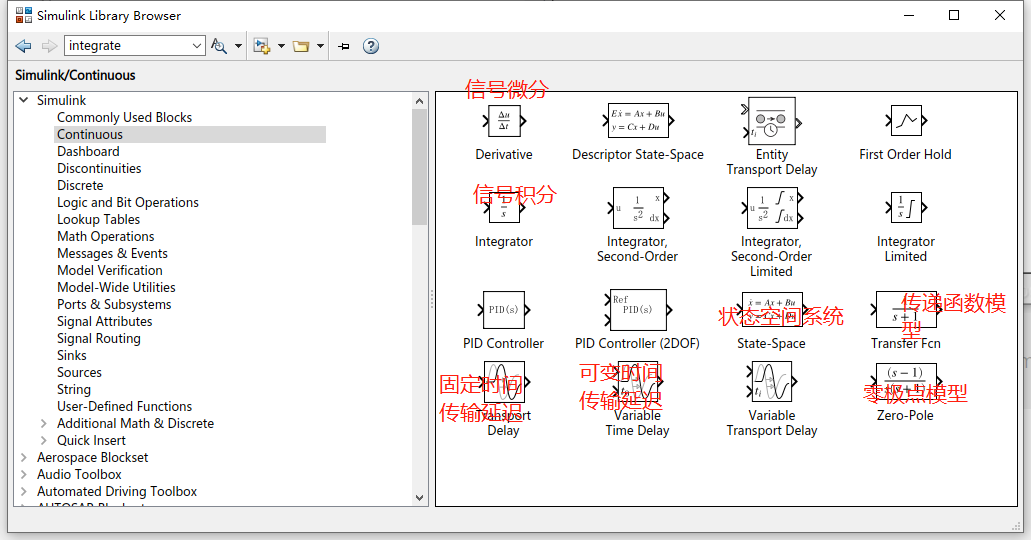
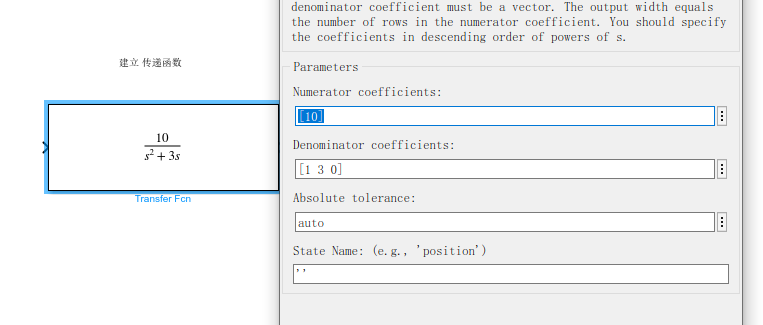
simulink 中模型与状态空间模型的转化

以状态空间形式线性化模型的函数命令： linmod(连续系统线性化) 和 dlinmod(离散系统线性化)，提供模型线性化时的操作点，返回的是 围绕操作点处系统线性化的状态空间模型。 将 simulink 系统转化为线性系统

需要注意的是：
在转化的时候，避免 simulink 中包 Derivative 模块和 Transport Delay 模块，分别应该使用 Simulink Extras 库下的 Linearization 子库中的 Switched derivative for linearization 模块和 Switched transport delay for linearization 模块代替 (见 课本的 p82 )

应用实例

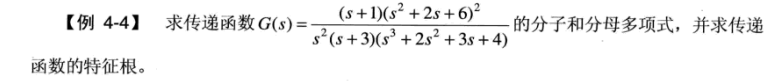
%% conv(u, v) 将两个多项式进行相乘
num = conv([1, 1], conv([1, 2, 6], [1, 2, 6]));
num
den = conv([1, 0, 0], conv([1, 3], [1, 2, 3, 4]));
den
r = roots(den); % 求特征方程的根
r

%% 传递函数表示：输出 u / 输入 y
num = [1, 4, 8];
den = [1, 11, 11, 10];
G = tf(num, den)
% 执行结果
G =
s^2 + 4 s + 8
------------------------
s^3 + 11 s^2 + 11 s + 10

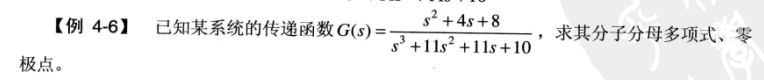
tf2zpk 将传递函数的分子和分母转化到 零极点增益模型 [z, p, k] = tf2zpk(num, den);

%% 求分子分母多项式、零极点
%% 表示 传递函数
num = [1, 4, 8];
den = [1, 11, 11, 10];
G = tf(num, den);
[tt, ff] = tfdata(G, 'v'); % 获取分子num和分母den
[z, p, k] = tf2zpk(num, den);
% 提取传递函数的零极点和增益
tt
ff
z
p
k

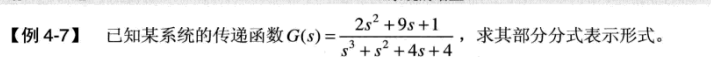
clear
clc
%% 求部分分式表示形式
num = [2, 0, 9, 1];
den = [1, 1, 4, 4];
[r, p, k] = residue(num, den)
% 求取系统的部分分式
% 执行结果：余数返回到向量r，极点返回到列向量p，常数项返回到k
r =
各个分式项的分子
-0.0000 - 0.2500i
-0.0000 + 0.2500i
-2.0000 + 0.0000i
p =	极点 各个分式项的分母
0.0000 + 2.0000i
0.0000 - 2.0000i
-1.0000 + 0.0000i
k = 常数项
2

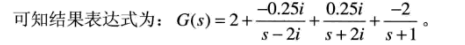
%% 求状态空间模型 ss()
A = [1 6 9 10; 3 12 6 8; 4 7 9 11; 5 12 13 14];
B = [4 6; 2 4; 2 2; 1 0];
C = [0 0 2 1; 8 0 2 2];
D = zeros(2,2);
G = ss(A, B, C, D)
% 执行结果
G =
A =
x1
x2
x3
x4
x1
1
6
9
10
x2
3
12
6
8
x3
4
7
9
11
x4
5
12
13
14
B =
u1
u2
x1
4
6
x2
2
4
x3
2
2
x4
1
0
C =
x1
x2
x3
x4
y1
0
0
2
1
y2
8
0
2
2
D =
u1
u2
y1
0
0
y2
0
0
Continuous-time state-space model.

这里的线性状态空间模型，需要使用 linmod 函数进行使用

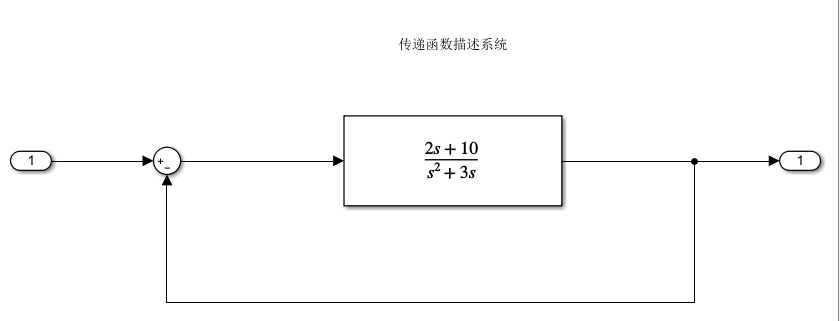
%% 传递函数 线性状态空间模型化
[A, B, C, D] = linmod('Demo4_9');
% 连续系统线性化 转化为状态空间模型

零极点模型：该传递函数的零点为 -5， 极点为 0和-3，增益为 2；

系统模型转换及连接

模型转换

在不同的场景下，使用的模型表示也不尽相同，所以，我们需要将模型之间进行相互的模型转换；转换关系图如下：xx2xx(sys)

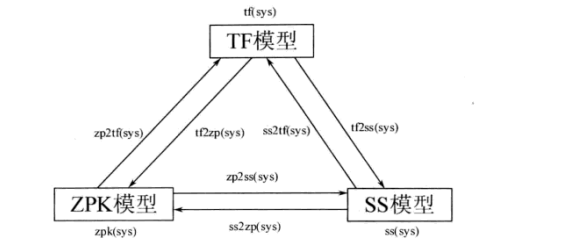
其中，tf表示传递函数，zp表示零极点模型；ss表示传递函数模型

clear;
clc
%% 将零极点模型转换为 传递函数模型和状态空间模型
% 使用的函数为：zp2tf(sys); zp2ss(sys)
z = -2;
p = [-1, -3, -5];
k = 6;
[num, den] = zp2tf(z, p, k);
[A, B, C, D] = zp2ss(z, p, k);
% 建立对应的模型
g_zpk = zpk(z, p, k)
g_tf = tf(num, den)
g_ss = ss(A, B, C, D)
% 执行结果
g_zpk =
6 (s+2)
-----------------
(s+1) (s+3) (s+5)
Continuous-time zero/pole/gain model.
g_tf =
6 s + 12
-----------------------
s^3 + 9 s^2 + 23 s + 15
Continuous-time transfer function.
g_ss =
A =
x1
x2
x3
x1
-1
0
0
x2
1
-8
-3.873
x3
0
3.873
0
B =
u1
x1
1
x2
1
x3
0
C =
x1
x2
x3
y1
0
0
1.549
D =
u1
y1
0
Continuous-time state-space model.

模型连接

串联连接

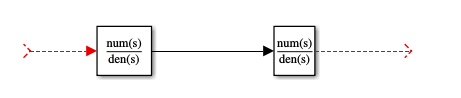
串联传递函数为 相乘

% num1, den1：第一个传递函数的分子和分母
% num2， den2：第二个传递函数的分子和分母
% num， den：串联后的传递函数的分子和分母
[num, den] = series(num1, den1, num2, den2);

并联连接

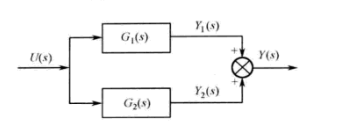
[num, den] = parallel(num1, den1, num2, den2);

反馈连接

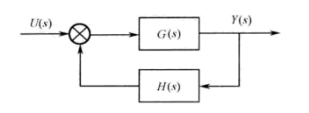
当系统为正反馈的时候，$$GH(s)=\frac{G(s)H(s)}{1-G(s)H(s)}$$
当系统为负反馈的时候，$$GH(s)=\frac{G(s)H(s)}{1+G(s)H(s)}$$

% sign 表示G(s)输入的连接符号，默认为 负值；表示系统H(s)输出到系统G(s)输入的连接符号
[num, den] = feedback(num1, den1, num2, den2, sign);

闭环连接

单位反馈连接，即 H(s) = 1 的一个特例

% sign 表示G(s)输入的连接符号，默认为 负值；表示系统H(s)输出到系统G(s)输入的连接符号
[numc, denc] = cloop(num, den, sign);

模型连接的 Matlab 实现

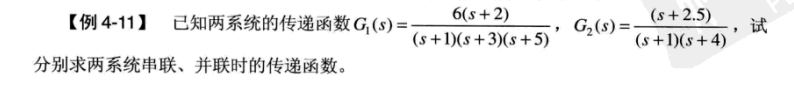
z1 = -2;
p1 = [-1, -3. -5];
k1 = 6;
[num1, den1] = zp2tf(z1, p1, k1);
z2 = -2.5;
p2 = [-1, -4];
k2 = 1;
[num2, den2] = zp2tf(z2, p2, k2);
[numS, denS] = series(num1, den1, num2, den2);
[numP, denP] = parallel(num1, den1, num2, den2);
GS = tf(numS, denS)
GP = tf(numP, denP)
% 执行结果
GS =
6 s^2 + 27 s + 30
--------------------------------------------
s^5 + 14 s^4 + 72 s^3 + 166 s^2 + 167 s + 60
Continuous-time transfer function.
GP =
s^4 + 17.5 s^3 + 87.5 s^2 + 156.5 s + 85.5
--------------------------------------------
s^5 + 14 s^4 + 72 s^3 + 166 s^2 + 167 s + 60
Continuous-time transfer function.

%% 反馈函数
num1 = [1, -1];
den1 = [1, -5, -2];
num2 = [1, 1];
den2 = [1, 3, 2];
H = 1;
% 闭环连接
[numc, denc] = cloop(num1, den1)
c_tf = tf(numc, denc)
% 负反馈函数
[numf, denf] = feedback(num1, den1,num2, den2);
f_tf = tf(numf, denf)
% 执行结果
c_tf =
s - 1
-------------
s^2 - 4 s - 3
Continuous-time transfer function.
f_tf =
s^3 + 2 s^2 - s - 2
-------------------------------
s^4 - 2 s^3 - 14 s^2 - 16 s - 5
Continuous-time transfer function.

非线性数学模型的线性化

线性系统满足叠加性和齐次性，反之则为非线性模型。我们需要将非线性系统进行线性化，方便我们处理。

在控制工程中，如果系统的运行是围绕平衡点进行的，并且系统中的信号是围绕平衡点变化的小信号，那么就可以用线性系统去近似非线性系统。这种线性系统在有限的工作范围内等价于原来的非线性系统。在控制工程中，这种线性化模型是很重要的。

线性化过程 是用数学方法来处理，将一个非线性函数 $y=f(x)$ ，在其工作点$(x_0,y_0)$ 处展开成泰勒级数，然后忽略其二次以上的高阶项得到线性化方程，并以此代替原来的非线性函数。

单输入单输出的函数：

设系统的输入量为 x(t), 输出量为y(t), 系统正常工作点为$y_0=f(x_0)$，则：
展开为：$$y=f(x_0)+(\frac{\mathrm{d}f(x)}{\mathrm{d}x}{)}_{x=x_0}(x-x_0)=y_0+K(x-x_0)$$ 该式表明，$y-y_0$与$x-x_0$成正比

对于多输入多输出的函数：
下面是两个输入变量的函数$y=f(x_1,x_2)$在工作点$x_1=x_{10}$,$x_2=x_{20}$处的线性化为例进行介绍：
方程 $y=f(x_1,x_2)$ 在工作点附近展开成泰勒级数如下：

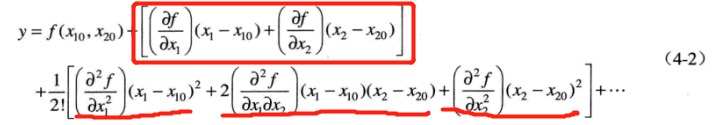
忽略高阶项：

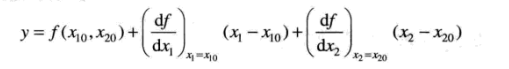
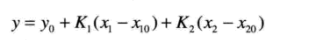
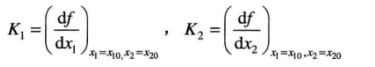
需要注意的是：
上面的线性化，只有在工作状态附近才是正确的。当工作状态的变化范围很大的时候，线性化方程就不合适了，这个时候，就必须使用非线性方程。

综合实例及matlab/simulink应用

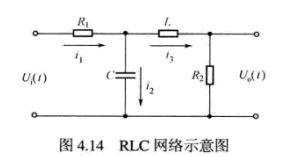
第一步：从数学上求出系统的传递函数：

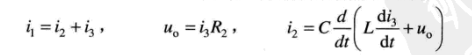
将上面的三个式子带入第一个微分方程中，得到：

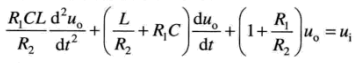
在零初始条件下，对上式去拉普拉斯变换，整理可得：


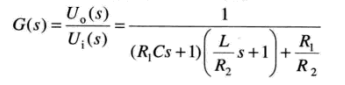
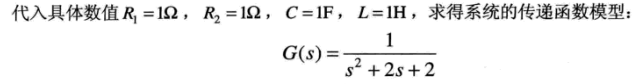
第二步：使用 matlab 建立系统模型：

clear all;
clc
num = [0 1];
den = [1 2 2];
sys_tf = tf(num, den)
[z, p, k] = tf2zp(num, den)
sys_zpk = zpk(z, p, k)
[A, B, C, D] = zp2ss(z, p, k);
sys_ss = ss(A, B, C, D)
%% 执行结果
sys_tf =
1
-------------
s^2 + 2 s + 2
Continuous-time transfer function.
z =
空的 0×1 double 列向量
p =
-1.0000 + 1.0000i
-1.0000 - 1.0000i
k =
1
sys_zpk =
1
--------------
(s^2 + 2s + 2)
Continuous-time zero/pole/gain model.
sys_ss =
A =
x1
x2
x1
-2
-1.414
x2
1.414
0
B =
u1
x1
1
x2
0
C =
x1
x2
y1
0
0.7071
D =
u1
y1
0
Continuous-time state-space model.

第三步：求取阶跃响应：

%% 画出任意一个动态系统模型sys的阶跃响应。这个模型可以是连续的或离散的,和单输入单输出或多输入多输出。
step(sys_tf);
grid on;

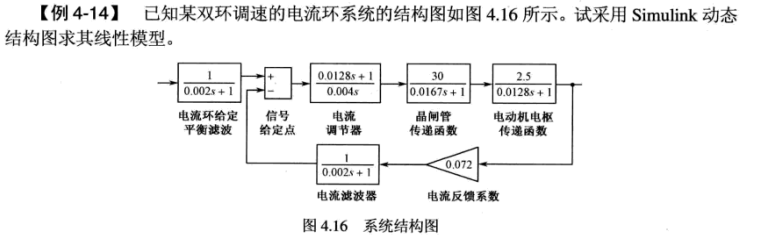
采用 simulink 动态结构图仿真的思路是：利用 simulink 提供的提取线性模型的函数 linmod() 或 linmod2(), 得到状态空间模型，然后就可以对状态空间模型进行各种仿真

步骤一：建立 simulink 动态结构图

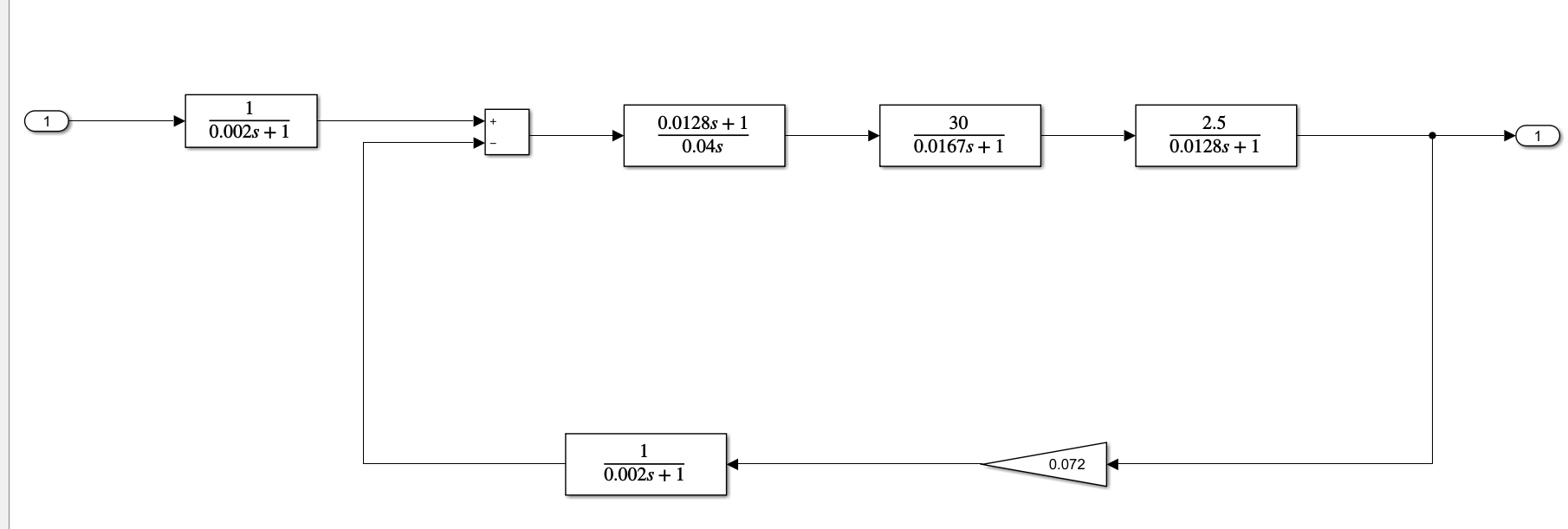
步骤二：求取系统的线性状态空间模型

%% 求取线性状态空间模型
[A, B, C, D] = linmod('Demo4_14')

步骤三：求系统的传递函数模型

%% 求系统的传递函数模型
[num, den] = ss2tf(A, B, C, D);
% prints the transfer function as a ratio of two polynomials in the transform variable 's' or 'z'. 将传递函数打印为转换变量's'或'z'中两个多项式的比率。
printsys(num, den, 's');
% 以传递函数形式显示出来
% 执行结果
A =
1.0e+03 *
-0.0781
0
0
0
1.7964
0
-0.5000
0
0
0
0.0141
0
-0.5000
0
0
0
0.5000
-0.5000
0
0
0
0.1600
-0.1600
0.0250
-0.0599
B =
0
1
0
0
0
C =
195.3125
0
0
0
0
D =
0
num/den =
56137724.5509 s^2 + 32454622005.988 s + 2192879865269.461
-----------------------------------------------------------------------------
s^5 + 1138.0052 s^4 + 392683.3832 s^3 + 43221369.7605 s^2 + 3506268712.5748 s
+ 157887350299.401

最后

以上就是失眠飞鸟为你收集整理的matlab simulink chapter4：控制系统的数学模型的全部内容，希望文章能够帮你解决matlab simulink chapter4：控制系统的数学模型所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。