Matlab编写函数实现牛顿迭代法，添加初值判定模块。若初值不满足选取条件，则重新输入初值；若累积n次初值不满足条件，则算法终止，输出异常信息。

牛顿迭代法相应的迭代函数为

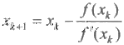
 只要把x₀选取得使f(x)和f”(x)同号，即f(x₀)×f"(x₀)>0,则迭代过程必收敛。

 在这里，我们先把函数默认看作连续可导的

函数中形式参数中有函数句柄F，我个人比较喜欢用matlabFunction来定义

比如函数，我们就可以用syms x;fx = exp(x)+10*x-2;

Fx=matlabFunction(fx);来转化为函数句柄带入运算。

具体函数如下

function x = Roots_newton( F,w,interMax)

% F为迭代函数的函数句柄，w误差,interMax最大迭代次数，x近似值

df=diff(sym(F)); %df是F的导数

df=matlabFunction(df);%df转化为函数句柄

df2=diff(sym(F),2);%df2是F的二阶导数

df2=matlabFunction(df2);

for i=1:3 % 进行初值判断，

    x0=input('请输入初值x0: ');

    if feval(F,x0)*feval(df2,x0)>0

        break

    else

        disp('初值不满足选取条件，则重新输入初值')

    end

    if i>3

        disp('达到最大错误次数')

        x=[];

        return  % 算法终止，输出异常信息

    end

end

x1=x0; %存储旧的近似值

x2=x1-feval(F,x1)/feval(df,x1); % x2存储新的近似值

n=1; % 迭代次数

    while abs(x2-x1)>=w && n<=interMax % 误差大于等于要求误差且次数小于最大迭代次数时， 继续迭代

        x1=x2;

        x2=x1-feval(F,x1)/feval(df,x1);

        n=n+1;

    end

x=x2;

end

最后

以上就是震动啤酒为你收集整理的Matlab编写函数实现牛顿迭代法，添加初值判定模块。若初值不满足选取条件，则重新输入初值；若累积n次初值不满足条件，则算法终止，输出异常信息。的全部内容，希望文章能够帮你解决Matlab编写函数实现牛顿迭代法，添加初值判定模块。若初值不满足选取条件，则重新输入初值；若累积n次初值不满足条件，则算法终止，输出异常信息。所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。