求柱的固有频率和欧拉屈曲荷载

clear
clc

disp('please wait!!!!!!-The job is under run')

% Discretizing the Beam

nel=50;                 % number of elements
nnel=2;                 % number of nodes per element
ndof=2;                 % number of dofs per node
nnode=(nnel-1)*nel+1;   % total number of nodes in system
sdof=nnode*ndof;        % total system dofs 

% Material properties
E=2.1*10^11;            % Youngs modulus
I=2003.*10^-8;          % moment of inertia of cross-section
mass = 61.3;            % mass density of the beam
tleng = 7.;             % total length of the beam
leng = tleng/nel;       % uniform mesh (equal size of elements)
lengthvector = 0:leng:tleng ;
% Boundary Conditions
bc = 'c-f' ;             % clamped-free
%bc = 'c-c' ;            % clamped-clamped
%bc = 'c-s' ;            % clamped-supported
%bc = 's-s' ;            % supported-supported

kk=zeros(sdof,sdof);    % initialization of system stiffness matrix
kkg=zeros(sdof,sdof);   % initialization of system geomtric stiffness matrix 
mm=zeros(sdof,sdof);    % initialization of system mass matrix 
index=zeros(nel*ndof,1);  % initialization of index vector

for iel=1:nel           % loop for the total number of elements

index=elementdof(iel,nnel,ndof);  % extract system dofs associated with element

[k,kg,m]=beam(E,I,leng,mass); % compute element stiffness,geometric
                                   % stiffness & mass matrix
                                   
kk=assembel(kk,k,index); % assemble element stiffness matrices into system matrix
kkg=assembel(kkg,kg,index); % assemble geometric stiffness matrices into system matrix
mm=assembel(mm,m,index); % assemble element mass matrices into system matrix

end
%
% Applying the Boundary conditions
[nbcd,bcdof] = BoundaryConditions(sdof,bc); % Reducing the matrix size
[kk,mm] = constraints(kk,mm,bcdof) ;
[kk,kkg] = constraints(kk,kkg,bcdof) ;
%
% Natural frequencies and Buckling load
[vecfreq freq]=eig(kk,mm);   % solve the eigenvalue problem for Natural Frequencies
freq = diag(freq) ;
freq=sqrt(freq);   % UNITS :rad per sec
freqHz = freq/(2*pi) ; % UNITS : Hertz
%
[vecebl ebl] = eig(kk,kkg);  % solve the eigenvalue problem for Buckling Loads
ebl = diag(ebl) ;
%
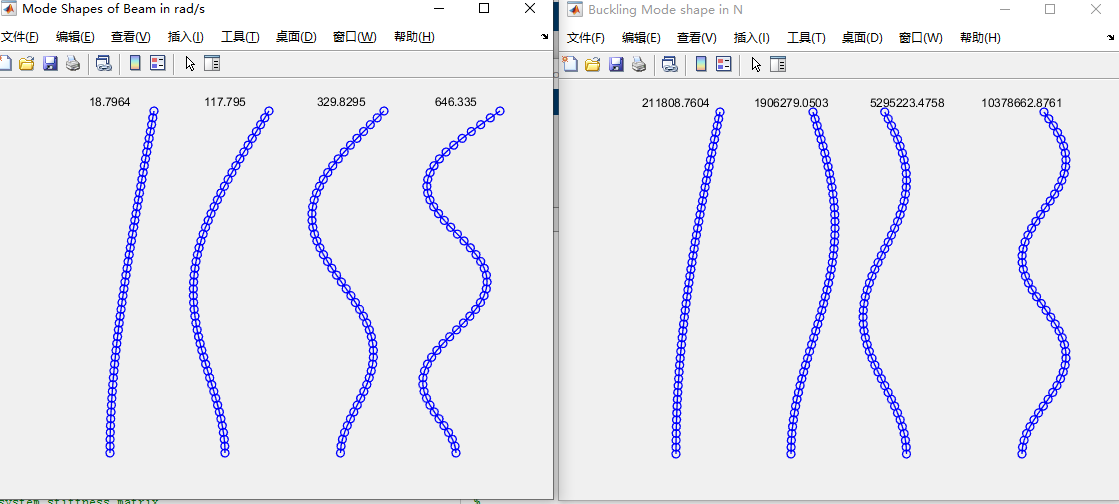
% Plot Mode Shapes
h = figure ;
set(h,'name','Mode Shapes of Beam in rad/s','numbertitle','off')
PlotModeShapes(vecfreq,freq,lengthvector,nbcd)
h = figure ;
set(h,'name','Buckling Mode shape in N','numbertitle','off')
PlotModeShapes(vecebl,ebl,lengthvector,nbcd)
%
% Theoretical Natural Frequencies
 [thfreq,thfreqHz,pcr] =  theory(bc,E,I,mass,tleng) ;

% Code validitation
theory = thfreq(1:3) ;
fem = freq(nbcd+1:nbcd+3);
error = (fem-theory)./theory*100;
compare = [theory fem error] ;
disp('First three natural frequencies (rad/sec)')
disp('theory        fem       error%')
disp('---------------------------------' )
disp(compare)
%
theory = pcr ;
fem = ebl(1);
error = (fem-theory)./theory*100 ;
compare = [theory fem error] ;
disp('Euler Buckling load (N)')
disp('theory        fem       error%')
disp('---------------------------------' )
disp(compare)

d146 

最后

以上就是微笑裙子为你收集整理的求柱的固有频率和欧拉屈曲荷载的全部内容，希望文章能够帮你解决求柱的固有频率和欧拉屈曲荷载所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。