1. 首页
  2. 文章中心
  3. 边缘计算

边缘计算卸载算法--LOPRTC

77 阅读 0 评论
我是靠谱客的博主 雪白大地，最近开发中收集的这篇文章主要介绍边缘计算卸载算法--LOPRTC，觉得挺不错的，现在分享给大家，希望可以做个参考。

概述

LOPRTC卸载算法

背景：我实现该算法是在边缘计算单个工作流环境中，下面可以看到此背景下的java代码实现。

1.算法伪代码在这里插入图片描述
2.输入

任务集等…

3.输出

接近最优的任务调度。

4.参数说明

在这里插入图片描述
1.MD：移动设备
2.RLTS：合理的基于本地的任务时间表
3.MEC服务器集S = {S1,S2,…,SM}
4.任务集T = {T1,T2,…,TN}
5.每个Job的处理时间P = {P0,P1,…,Pn-1}
6.某设备的行走路径：P = {(Au1,tu1),(Au2,tu2),…(Aup,tup)}，其中tu是一个任意的时间点。
7.移动设备集S0 = {SM+1,SM+2,…,SM+L}
8.一个区域A = {Au}
9.整数q
10.dj：工作流任务最长执行时间

5.分析
  1. 算法2-5行：将N个任务划分成N/q(向上取整)个组。1<= q <= N
  2. 算法6-17行：任务调度优化，For 0≤k≤(N / q), 计算局部最优任务调度
    ① 计算第 k 组中所有任务的最早开始时间与完成所有任务的最晚结束时间（第k组的最晚结束时间是第 k+1 组的最早开始时间）。
    ② 为第 k 组中的每个任务 Tj 计算候选卸载MEC服务器集CSj，每个任务 Tj 可以卸载到覆盖其行走路径的MEC服务器，在时间间隔[第k组的最早开始时间, min {dj, 第k组的最晚结束时间}]。
    ③ 计算第 k 组任务的局部最优任务调度（利用分支限界法）。
  3. 算法18行：通过这些局部最优任务调度，计算所有任务（各组的并集）的近似最优任务调度。
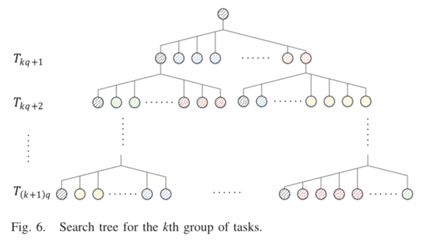
    在这里插入图片描述

本质：还是类似枚举，只是利用时间限制剪掉了一些情况的组合。

6.我的java代码实现
/**
* 初始化的方法
* 初始化任务的邻接矩阵，任务、组的最早开始时间与最晚结束时间
*/
void LOPRTCInit(){
// 卸载策略数组初始化
offloadStra = new int[taskNum];
for (int i = 0; i < taskNum; i++) {
offloadStra[i] = 0;
}
// 邻接矩阵初始化
task_depen = new int[taskNum][taskNum];
for (int i = 0; i < taskNum; i++) {
for (int j = 0; j < taskNum; j++) {
task_depen[i][j] = 0;
}
}
try{
SAXReader reader = new SAXReader();// 创建SAXReader对象用于读取xml文件
Document doc = reader.read(new File(path));// 读取xml文件，获得Document对象
Element root = doc.getRootElement();
List<Element> childElements = root.elements("child");// 获取根元素下的所有child标签的子元素
for (int i = 0; i < childElements.size(); i++) {
String vex_str = childElements.get(i).attributeValue("ref");
int vex_int = Integer.parseInt(vex_str.substring(2));
List<Element> parents = childElements.get(i).elements("parent");// 获取child元素下的所有parent标签元素
for (int j = 0; j < parents.size(); j++) {
String vex_parent_str = parents.get(j).attributeValue("ref");
int vex_parent_int = Integer.parseInt(vex_parent_str.substring(2));
task_depen[vex_parent_int][vex_int] = 1;
}
}
}catch(Exception e){
System.out.println("xml没找到！");
}
// 每个任务的执行时间初始化
task_exec = new double[taskNum];
try{
SAXReader reader = new SAXReader();// 创建SAXReader对象用于读取xml文件
Document doc = reader.read(new File(path));// 读取xml文件，获得Document对象
Element root = doc.getRootElement();
List<Element> jobElements = root.elements("job");// 获取根元素下的所有job标签的子元素
for (int i = 0; i < jobElements.size(); i++) {
String vexStr = jobElements.get(i).attributeValue("id");
int vexInt = Integer.parseInt(vexStr.substring(2));
String timeStr = jobElements.get(i).attributeValue("runtime");
double timeDouble = Double.parseDouble(timeStr);
task_exec[vexInt] = timeDouble;
}
}catch(Exception e){
System.out.println("xml没找到！");
}
// 每个任务的EST、EFT矩阵初始化
task_time = new double[taskNum][2];
int count = 0;// 辅助变量
for (int k = 0; k < taskNum; ++k) {
for (int j = 0; j < taskNum; j++) {// 初始化开始节点的EST、EFT
if (task_depen[j][k] == 0) {
++count;
}
}
if (count == taskNum) {
task_time[k][0] = 0;
task_time[k][1] = task_exec[k];
for (int j = 0; j < taskNum; j++) {// 初始化开始节点直接后继节点的EST、EFT
if (task_depen[k][j] == 1) {
if (task_time[j][0] < task_time[k][1]) {
task_time[j][0] = task_time[k][1];
task_time[j][1] = task_time[j][0] + task_exec[j];
}
}
}
}
count = 0;
}
for (int k = 0; k < taskNum; ++k) {// 初始化剩下的所有节点的EST、EFT
for (int j = 0; j < taskNum; j++) {
if (task_depen[k][j] == 1) {
if (task_time[j][0] < task_time[k][1]) {
task_time[j][0] = task_time[k][1];
task_time[j][1] = task_time[j][0] + task_exec[j];
}
}
}
}
// 计算分几组
if(taskNum % 6 == 0){// 分6组
groupStartTime = new double[6];
groupEndTime = new double[6];
}else{
groupStartTime = new double[7];
groupEndTime = new double[7];
}
// 测试输出
/*for (int i = 0; i < taskNum; i++) {
for (int j = 0; j < 2; j++) {
System.out.print(task_time[i][j] + " ");
}
System.out.println();
}
System.out.println();*/
// 计算每组的最早开始时间，最晚结束时间
try{
for (int i = 0; i < groupStartTime.length; i++) {
double minStart = task_time[i*q][0];
for (int j = i*q; j<(i+1)*q && j<taskNum; j++) {
if(minStart > task_time[j][0]){
minStart = task_time[j][0];
}
}
groupStartTime[i] = minStart;
}
}catch (Exception e){
System.out.println("数组下标越界异常！");
}
for (int i = 0; i < groupEndTime.length-1; i++) {
groupEndTime[i] = groupStartTime[i+1];
}
double maxEnd = task_time[0][1];
for (int i = 1; i < taskNum; i++) {
if(task_time[i][1] > maxEnd){
maxEnd = task_time[i][1];
}
}
groupEndTime[groupEndTime.length-1] = maxEnd;
}
/**
* 找出某组任务的局部最优卸载策略
* @param indexOfGroup 某组任务的索引下标（第一组任务对应下标为0）
*/
void groupOptimal(int indexOfGroup){
// 依次是卸载到云层、雾层、本地
double time1 = 0, time2 = 0, time3 = 0;
double energy1 = 0, energy2 = 0, energy3 = 0;
powerModel = (FogLinearPowerModel) getmobile().getHost().getPowerModel();
// 获取云、雾、终端层的平均Mips
double cAvgMips = getcloud().getAverageMips();
double fAvgMips = getFogNode().getAverageMips();
double mAvgMips = getmobile().getAverageMips();
try{
for (int i = indexOfGroup*q; i<(indexOfGroup+1)*q && i<taskNum; i++) {
Job job = joblist.get(i);
time1 = job.getCloudletLength() / cAvgMips
+ getJobFileSize(job) / parameter / WAN_Bandwidth;
//卸载所需能耗 = 空闲功率 * 云执行时间 + 传输功率 * (发送数据大小 + 接收数据大小 ) / WAN带宽
energy1 = powerModel.getStaticPower() * job.getCloudletLength() / cAvgMips
+ powerModel.getSendPower() * getJobFileSize(job) / parameter / WAN_Bandwidth;
time2 = job.getCloudletLength() / fAvgMips
+ getJobFileSize(job) / parameter / LAN_Bandwidth;
energy2 = powerModel.getStaticPower() * job.getCloudletLength() / fAvgMips
+ powerModel.getSendPower() * getJobFileSize(job) / parameter / LAN_Bandwidth;
time3 = job.getCloudletLength() / mAvgMips;
energy3 = powerModel.getMaxPower() * job.getCloudletLength() / mAvgMips;
double minTimeSpan = Math.min(deadline,groupEndTime[indexOfGroup]-groupStartTime[indexOfGroup]);
if(minTimeSpan < Math.min(time1, time2)){// 都不满足时间约束
job.setoffloading(getmobile().getId());
}else if(minTimeSpan > Math.max(time1, time2)){// 都满足时间约束，根据优化目标选择卸载到哪
switch (optimize_objective){
case "Time":
if(Math.min(time1, Math.min(time2, time3)) == time1){
offloadStra[i] = 2;// 卸载到云
}else if(Math.min(time1, Math.min(time2, time3)) == time2){
offloadStra[i] = 1;// 卸载到雾
}else{
offloadStra[i] = 0;// 不卸载
}
break;
case "Energy":
if(Math.min(energy3, Math.min(energy1, energy2)) == energy1){
offloadStra[i] = 2;
}
else if(Math.min(energy3, Math.min(energy1, energy2)) == energy2){
offloadStra[i] = 1;
}
else{
offloadStra[i] = 0;
}
break;
default:
break;
}
}else{//minTimeSpan介于time1和time2之间
if(minTimeSpan > time1 && minTimeSpan < time2){// 根据优化目标选择卸载到云或不卸载
switch (optimize_objective){
case "Time":
if(Math.min(time1, time3) == time1){
offloadStra[i] = 2;
}else{
offloadStra[i] = 0;
}
break;
case "Energy":
if(Math.min(energy1, energy3) == energy1){
offloadStra[i] = 2;
}else{
offloadStra[i] = 0;
}
break;
default:
break;
}
}else{// 根据优化目标选择卸载到雾或不卸载
switch (optimize_objective){
case "Time":
if(Math.min(time2, time3) == time2){
offloadStra[i] = 1;
}else{
offloadStra[i] = 0;
}
break;
case "Energy":
if(Math.min(energy2, energy3) == energy2){
offloadStra[i] = 1;
}else{
offloadStra[i] = 0;
}
break;
default:
break;
}
}
}
}
}catch (Exception e){
System.out.println("数组下标越界异常！");
}
}
@Override
public void BeforeOffloading(double deadline) {
this.deadline = deadline;
LOPRTCInit();
joblist = getjobList();
for (int i = 0; i < groupStartTime.length; i++) {
groupOptimal(i);
}
}

最后

以上就是雪白大地为你收集整理的边缘计算卸载算法--LOPRTC的全部内容，希望文章能够帮你解决边缘计算卸载算法--LOPRTC所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。

本图文内容来源于网友提供，作为学习参考使用，或来自网络收集整理，版权属于原作者所有。
点赞(51)

相关文章

移动边缘计算的三级卸载机制心得体会与讲解（一）
移动边缘计算的三级卸载机制心得体会与讲解（一）
论文笔记
论文笔记
python毕设选题 - 毕业设计题目推荐一、python 毕设 选题推荐二、选题注意事项三、开题指导四、最后
python毕设选题 - 毕业设计题目推荐一、python 毕设 选题推荐二、选题注意事项三、开题指导四、最后
移动边缘计算——计算卸载一  边缘计算产生背景二  移动边缘计算三  计算卸载
移动边缘计算——计算卸载一  边缘计算产生背景二  移动边缘计算三  计算卸载
边缘计算卸载算法--LOPRTC
边缘计算卸载算法--LOPRTC
【动力学】汽车性能仿真系统含Matlab源码
【动力学】汽车性能仿真系统含Matlab源码
几种边缘检测算法对比及python代码实现1、Sobel算子2、Canny算子3、Laplacian算子
几种边缘检测算法对比及python代码实现1、Sobel算子2、Canny算子3、Laplacian算子
边缘计算卸载算法--CD梯度下降
边缘计算卸载算法--CD梯度下降

评论列表共有 0 条评论

立即
投稿
返回
顶部