贝叶斯机器学习 – 动态夏普比率和配对交易
在本章中,我们将介绍机器学习 (ML) 的贝叶斯方法以及它们在开发和评估交易策略时,对不确定性的看法会增加这一看法原本价值的不同之处。
贝叶斯统计使我们能够量化未来事件的不确定性,并在一个新信息出现时用一个原则性方式定义我们的预测。这种动态方法很好地适应了不断发展的金融市场。当相关数据较少并且我们需要系统地整合先验知识或假设时,它特别有用。
我们将看到机器学习的贝叶斯方法可以围绕统计指标、参数估计和预测更丰富地洞察不确定性。应用范围从更多精细风险管理,以动态更新包含市场变化的预测模型环境。 Black-Litterman 资产配置方法(参见第 5 章,投资组合优化和性能评估)可以解释为贝叶斯模型。它计算资产的预期回报作为市场均衡和投资者观点的平均值,通过每项资产的波动性、跨资产相关性以及每个预测的置信度。
更具体地说,在本章中,我们将介绍:
- 贝叶斯统计如何应用于机器学习
- 使用 PyMC3 进行概率编程
- 使用 PyMC3 定义和训练 ML模型
- 如何运行最先进的采样方法来进行近似推理
- 用于计算动态夏普比率、动态配对交易对冲比率的贝叶斯 ML 应用程序,并估计随机波动率
贝叶斯机器学习的工作原理
据说古典统计遵循频率论方法,因为它将概率解释为从长远来看,即在观察大量试验之后,事件的相对频率。在概率的上下文中,事件是实验的一个或多个基本结果的组合,例如掷两个骰子的六个相等结果中的任何一个或资产价格下跌 10%。
相比之下,贝叶斯统计将概率视为对事件发生信心的测量方法。因此,贝叶斯视角为主观观点和意见分歧大于频率解释。这种差异对于以下事件最为显著:发生的频率不足以达到长期频率的客观衡量标准。
换句话说,频率统计假设数据是来自总体的随机样本,旨在确定生成数据的固定参数。反过来,贝叶斯统计将数据视为给定的,并将参数视为具有可从数据推断出的分布的随机变量。作为结果,频率论方法至少需要与要处理的参数一样多的数据点估计的。另一方面,贝叶斯方法与较小的数据集兼容,并且非常适合一次从一个样本进行在线学习。
贝叶斯视图对于许多罕见或独特的现实世界事件非常有用。比如下一次选举的结果或市场是否会3个月内崩溃。在每种情况下,随着事件的临近都有相关的历史数据和独特的情况出现。
首先我们将介绍贝叶斯定理,通过将先前的假设与新的经验证据相结合,将更新信念的概念具体化,并将由此产生的参数估计与他们的频率结合。然后我们将展示贝叶斯统计推断的两种方法,即共轭先验和近似推理,可以深入了解后验分布潜在的(即未观察到的)参数,例如期望值:
- 共轭先验通过提供封闭形式的解决方案来促进更新过程,使我们能够精确计算解。然而,这种精确的分析方法并不总是可用的。
- 近似推理模拟由组合假设和数据产生的分布并使用来自该分布的样本来计算统计见解。
拓展
最常见应用场景
文本分类/垃圾文本过滤/情感判别:这大概会朴素贝叶斯应用做多的地方了,即使在现在这种分类器层出不穷的年代,在文本分类场景中,朴素贝叶斯依旧坚挺地占据着一席之地。因为多分类很简单,同时在文本数据中,分布独立这个假设基本是成立的。而垃圾文本过滤(比如垃圾邮件识别)和情感分析(微博上的褒贬情绪)用朴素贝叶斯也通常能取得很好的效果。
多分类实时预测:这个是不是不能叫做场景?对于文本相关的多分类实时预测,它因为上面提到的优点,被广泛应用,简单又高效。
推荐系统:是的,你没听错,是用在推荐系统里!!朴素贝叶斯和协同过滤(Collaborative Filtering)是一对好搭档,协同过滤是强相关性,但是泛化能力略弱,朴素贝叶斯和协同过滤一起,能增强推荐的覆盖度和效果。
————————————————
版权声明:本文为CSDN博主「liuzheng081」的原创文章,遵循CC 4.0 BY-SA版权协议,转载请附上原文出处链接及本声明。
原文链接:https://blog.csdn.net/liuzheng081/article/details/81166720
如何根据经验证据更新假设
“当事实改变时,我会改变主意。你要做什么,先生?”
——约翰·梅纳德·凯恩斯
托马斯·贝叶斯牧师在 250 多年前提出的定理,使用基本的概率论来规定概率或信念应该如何作为相关的新信息而改变到达。前面的凯恩斯引文抓住了这种精神。它依赖于条件和总概率和链式法则;参见 Bishop (2006) 和 Gelman 等人。 (2013) 介绍和更多。概率信念涉及单个参数或参数向量(也:假设)。每个参数可以是离散的或连续的。可能是一维统计数据,如(离散)模式分类变量或(连续)均值,或更高维的值集,如协方差矩阵或深度神经网络的权重。
与频率统计的一个主要区别是贝叶斯假设表示为概率分布而不是参数值。因此,虽然频率论者的推理侧重于点估计,贝叶斯推理产生概率分布。贝叶斯定理通过计算后验概率来更新关于感兴趣参数的信念来自以下输入的概率分布,如图 10.1 所示:
- 先验分布表明我们考虑每个可能的假设的可能性。
- 当给定某些值时,似然函数输出观察数据集的概率参数 ,即针对特定假设。
- 考虑到所有可能的假设,证据衡量观察到的数据的可能性。因此,它是所有参数值都相同,用于对分子进行归一化。
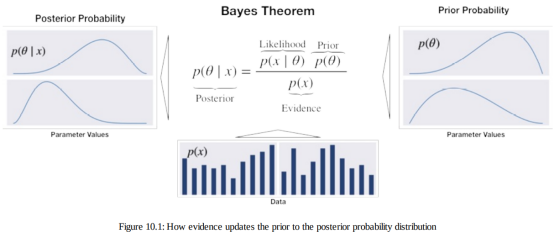
后验是先验和可能性的乘积,除以证据。 因此,它反映了假设的概率分布,通过考虑先验假设和数据。 从不同的角度来看,后验概率是应用链式法则的结果,反过来,分解数据和参数的联合分布。对于更高维的连续变量,公式变得更加复杂并且涉及(多个)积分。 此外,另一种公式使用赔率将后验赔率表示为先验几率的乘积乘以似然比(参见 Gelman 等人,2013 年)。
精确推理——最大后验估计
贝叶斯规则在精确计算后验概率方面的实际应用非常有限。这是因为分母中证据项的计算非常具有挑战性。证据反映了所有可能参数值上观察到的数据的概率。它也被称为边际可能性,因为它需要通过添加或“边缘化”参数的分布整合他们的分布。这通常仅在具有假设值很少的离散参数的简单情况下才有可能。
最大后验概率 (MAP) 估计利用了这样一个事实,即证据是一个常数因子,可以缩放后验以满足概率分布的要求。 由于证据不依赖于θ,后验分布与似然和先验的乘积成正比。 因此,MAP估计选择使给定观察数据和先验信念的后验最大化的值θ,即后验模式。
MAP 方法与参数的最大似然估计 (MLE) 形成对比,定义概率分布。 MLE 选择对于观察到的训练数据使似然函数最大化的参数值θ。
定义的外观突出显示 MAP 与 MLE 的不同之处在于它包括了先验分布。在换句话说,除非先验是一个常数,否则 MAP 估计将与其 MLE 对应物不同:
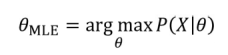
MLE 解决方案倾向于反映频率论的概念,即概率估计应该反映观察到的比率。另一方面,先验对 MAP 估计的影响通常对应于添加数据这反映了对 MLE 的先前假设。例如,硬币有偏见的强先验可以是通过添加倾斜的试验数据纳入 MLE 上下文。
先验分布是贝叶斯模型的关键组成部分。现在我们将介绍一些方便的有助于分析推理的选择。
如何选择先验
先验应该反映有关参数分布的知识,因为它会影响 MAP估计。如果不确定先验,我们需要做出选择,通常是从几个合理的选项。一般而言,好的做法是测试先验并检查稳健性,替代方案是否会导致相同的结论。。
先验有几种类型:
- 客观先验最大化数据对后验的影响。如果参数分布为未知,我们可以选择一个无信息先验,如均匀分布,也称为平坦先验,在相关的参数值范围内。
- 相比之下,主观先验旨在将模型外部的信息合并到估计中。在 Black-Litterman 背景下,投资者对资产未来回报的信念将是主观先验的例子。
- 经验先验结合了贝叶斯和频率论方法,并使用历史数据来消除主观性,例如,通过估计各种矩来拟合标准分布。使用一些每日回报的历史平均值而不是对未来回报的信念将是一个例子的简单的经验先验。
在 ML 模型的上下文中,先验可以被视为正则化器,因为它限制了后验可以假设。例如,先验概率为零的参数不属于后验分布。一般来说,更好的数据可以得出更有力的结论并减少前人的影响。
如何保持推理简单——共轭先验
当结果后验相同时,先验分布与似然共轭类或分布族作为先验,除了不同的参数。例如,当两个先验和似然是正态分布的,那么后验也是正态分布的。先验和似然的共轭意味着后验的封闭形式解决方案,有利于更新过程并避免需要使用数值方法来近似后验。而且,得到的后验可以用作下一个更新步骤的先验。
让我们使用股票价格变动的二元分类示例来说明这个过程。
资产价格变动的动态概率估计
当数据由为了积极的结果有一定成功概率的二元伯努利随机变量组成时,重复试验的成功次数服从二项式分布。这共轭先验是支持区间 [0, 1] 和两个形状参数的 beta 分布对成功概率的任意先验分布进行建模。因此,后验分布也是我们可以通过直接更新参数来推导出 beta 分布。
我们将收集不同规模的每日标准普尔 500 指数二值化回报样本,其中正结果是价格上涨。从一个无信息先验开始,为每个人分配相等的概率区间 [0, 1] 中可能的成功概率,我们计算不同证据的后验样品。
以下代码示例显示更新包括简单地将观察到的成功和失败次数添加到先验分布的参数中以获得后验
n_days = [0, 1, 3, 5, 10, 25, 50, 100, 500]
outcomes = sp500_binary.sample(n_days[-1])
p = np.linspace(0, 1, 100)
# uniform (uninformative) prior
a = b = 1
for i, days in enumerate(n_days):
up = outcomes.iloc[:days].sum()
down = days - up
update = stats.beta.pdf(p, a + up , b + down)
由此产生的后验分布已绘制在下图中。 它们说明了从将所有成功概率视为同等可能性的统一先验进化到越来越多的成功概率峰分布。
在 500 个样本之后,概率集中在从 2010 年到 2017 年 54.7%的正移动的实际概率附近。它还显示了 MLE 和 MAP 估计之间的微小差异,其中后者倾向于被略微拉向一致先验的预期值
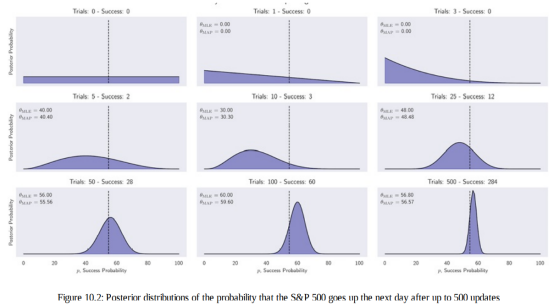
在实践中,共轭先验的使用仅限于低维情况。此外,简化的MAP 方法避免计算证据项,但有一个关键的缺点,即使它可用:它不返回分布,因此我们可以得出不确定性的度量或将其用作先验。 因此,我们需要使用数值方法和随机方法进行近似而不是精确的推理模拟,我们将在接下来介绍。
确定性和随机近似推理
对于大多数与实际相关的模型,将无法推导出精确的后验分布分析并计算潜在参数的期望值。模型可能有太多参数,或者后验分布对于解析解可能过于复杂:
- 对于连续变量,积分可能没有封闭形式的解,而空间的维数和被积函数的复杂性可能会禁止数值积分。
- 对于离散变量,边缘化涉及对所有可能的配置求和隐藏变量,虽然这在原则上总是可能的,但我们在实践中经常发现可能是指数级的许多隐藏状态,这使得这个计算变得非常昂贵。
尽管对于某些应用程序,未观察到的参数的后验分布会很有趣,大多数情况下,主要需要评估预期,例如进行预测。在这样的在某些情况下,我们可以依靠近似推理,其中包括随机和确定性方法:
- 基于马尔可夫链蒙特卡罗(MCMC)采样的随机技术已经普及在许多领域中使用贝叶斯方法。它们通常具有收敛到确切的结果。在实践中,采样方法可能在计算上要求很高,并且通常仅限于小规模的问题。
- 称为变分推理或变分贝叶斯的确定性方法基于分析后验分布的近似值,可以很好地扩展到大型应用程序。他们做了简化假设,例如,后验以特定方式分解或它具有特定的参数形式,例如高斯。因此,它们不会产生准确的结果,并且可以用作抽样方法的补充。
我们将在以下两节中概述这两种方法。
马尔可夫链蒙特卡罗采样
抽样是关于绘制样本 X=(x1, ..., xn) 来自给定的分布 p(x)。假设样本是独立的,大数定律确保对于越来越多的样本,给定实例 xi在样本中(对于离散情况)对应于它的概率 p(x=xi)。在里面连续情况下,类似的推理适用于样本空间的给定区域。因此,平均过样本可以用作分布参数期望值的无偏估计量。
一个实际挑战包括确保独立采样,因为分布未知。相关样本可能仍然是无偏的,但往往会增加估计的方差,因此更多与独立样本一样精确的估计需要样本。
随着状态数量的增加,从多元分布中采样在计算上要求很高与维数呈指数关系。许多算法促进了这个过程;我们将在这里介绍一些基于 MCMC 的方法的流行变体。
马尔可夫链是一个动态随机模型,它描述了一组状态上的随机游走由转移概率连接。马尔可夫性质规定进程没有内存,下一步只取决于当前状态。换句话说,这取决于现在是否,过去和未来是独立的,即关于过去状态的信息无助于预测未来超出了我们现在所知道的。
蒙特卡罗方法依靠重复随机抽样来近似结果确定性的,但不允许精确的解析解。它是在曼哈顿时期发展起来的在原子水平上估算能量的项目,并获得了其经久不衰的代号,以确保保密。许多算法将蒙特卡罗方法应用于马尔可夫链,一般如下进行:
1. 从当前位置开始
2. 从提案分布中绘制一个新位置
3.根据数据和先验分布评估新职位的概率
a.如果有足够的可能,移至新职位
b.否则,保持在当前位置
4. 从第 1 步开始重复
5.经过给定次数的迭代,返回所有接受的位置
MCMC 方法旨在识别和探索集中显着概率密度的后验有趣区域。 当无记忆过程始终通过附近接受率增加的后验的高概率状态时,它就会收敛。一个关键的挑战是平衡随机探索样本空间的需求与降低接受率的风险。
该过程的初始步骤可能比后部更能反映起始位置,并且通常作为老化样本被丢弃。 一个关键的 MCMC 属性是,在一定(但未知)的迭代次数之后,进程应该“忘记”它的初始位置。
剩余的样本称为过程的痕迹。假设收敛,相对频率的样本近似后验,可用于计算基于大数定律的期望值。
如前所述,估计的精度取决于样本的序列相关性由随机游走收集,根据设计,每一个都只取决于之前的状态。更高相关性限制了对后验的有效探索,需要进行诊断测试。
设计这种马尔可夫链的一般技术包括 Gibbs 采样、Metropolis-Hastings算法,以及最近的哈密顿 MCMC 方法,它们往往表现更好。
吉布斯抽样
吉布斯抽样将多元抽样简化为一维抽签序列。从一些起点,它在对 nth 个变量进行采样时迭代地保持 n-1个变量不变。它包含这个样本并重复它。
该算法非常简单且易于实现,但产生的高度相关样本会减慢向下收敛。顺序性质也阻止了并行化。参见 Casella 和 George (1992)以获得详细的描述和解释。
延伸:
吉布斯采样的通俗解释?
问题是我们不知道p(E,T,W),或者说,不知道三件事的联合分布joint distribution。当然,如果知道的话,就没有必要用gibbs sampling了。但是,我们知道三件事的conditional distribution。也就是说,p(E|T,W),p(T|E,W),p(W|E,T)。现在要做的就是通过这三个已知的条件分布,再用gibbs sampling的方法,得到联合分布。
具体方法。首先随便初始化一个组合,i.e. 学习+晚上+刮风,然后依条件概率改变其中的一个变量。具体说,假设我们知道晚上+刮风,我们给E生成一个变量,比如,学习-》吃饭。我们再依条件概率改下一个变量,根据学习+刮风,把晚上变成上午。类似地,把刮风变成刮风(当然可以变成相同的变量)。这样学习+晚上+刮风-》吃饭+上午+刮风。同样的方法,得到一个序列,每个单元包含三个变量,也就是一个马尔可夫链。然后跳过初始的一定数量的单元(比如100个),然后隔一定的数量取一个单元(比如隔20个取1个)。这样sample到的单元,是逼近联合分布的。
————————————————
版权声明:本文为CSDN博主「-柚子皮-」的原创文章,遵循CC 4.0 BY-SA版权协议,转载请附上原文出处链接及本声明。
原文链接:https://blog.csdn.net/pipisorry/article/details/51373090
Metropolis-Hastings抽样
Metropolis-Hastings 算法根据其当前状态随机提出新位置。它这样做有效探索样本空间,降低样本相对于吉布斯采样的相关性。为了确保它从后验采样,它使用先验和似然,与后验成正比。它以取决于结果的概率接受相对于当前样本的相应值。提案评估方法的一个主要好处是它使用比例而不是精确后验评估。但是,收敛可能需要很长时间。这是因为与后验无关的随机运动会降低接受率,从而导致大量步骤仅产生少量(潜在相关)样本。接受率可以调整通过减少提议分布的方差,但由此产生的更小的步长意味着更少勘探。
有关该算法的详细介绍性说明,请参见 Chib 和 Greenberg (1995)。
Hamiltonian Monte Carlo – going NUTS
哈密顿蒙特卡罗 (HMC) 是一种利用一阶导数似然梯度信息的混合方法。有了这个,它提出了新的探索和状态克服了一些 MCMC 挑战。此外,它还结合了动力来有效地“跳跃”围绕”后验。因此,它比高维目标分布更快地收敛更简单的随机游走 Metropolis 或 Gibbs 采样。参见 Betancourt (2018)概念介绍。
No U-Turn Sampler (NUTS, Hoffman and Gelman 2011) 是一个自调整的 HMC 扩展在选择建议之前,自适应地调节后验周围移动的大小和数量。它适用于高维和复杂的后验分布,并允许许多复杂的模型在没有关于拟合算法本身的专业知识的情况下进行拟合。正如我们将在接下来看到的部分,它是 PyMC3 中的默认采样器。
变分推理和自动微分
变分推理 (VI) 是一种通过优化来近似概率密度的 ML 方法。在贝叶斯上下文中,它近似后验分布,如下:
1. 选择一个参数化的概率分布族
2. 找到最接近目标的家庭成员,由Kullback-Leibler背离衡量
与 MCMC 相比,变分贝叶斯趋于收敛更快,并且可以更好地扩展到大数据。尽管MCMC 用最终任意收敛的链中的样本来近似后验接近目标,变分算法近似后验与优化的结果不保证与目标一致。
变分推理更适合大型数据集,例如数亿文本文档,因此我们可以快速探索许多模型。相比之下,MCMC 将提供更准确的在较小的数据集上或当时间和计算资源造成较少限制时的结果。例如,如果你花了 20 年时间收集一个小而昂贵的东西,MCMC 将是一个不错的选择数据集,确信您的模型是合适的,并且您需要精确的推理。Salimans,Kingma 和 Welling (2015) 进行了更详细的比较。
变分推理的缺点是需要特定于模型的推导和实现定制的优化例程,这会减慢广泛采用的速度。
最近的自动微分变分推理 (ADVI) 算法使这个过程自动化这样用户只需指定型号,表示为程序,ADVI 自动生成一个相应的变分算法。我们将看到 PyMC3 支持各种变分推理技术,包括 ADVI。
用于性能比较的贝叶斯夏普比率
在本节中,我们将说明:
如何使用 PyMC3 将夏普比率 (SR) 定义为概率模型
如何比较不同收益序列的后验分布
两个系列的贝叶斯估计提供了非常丰富的见解,因为它提供了效应大小、组 SR 均值及其差异以及标准偏差及其差异的可信值的完整分布。 Python 实现归功于 Thomas Wiecki,并受到 R 包 BEST(Meredith 和 Kruschke,2018)的启发。
贝叶斯 SR 的相关用例包括分析替代策略之间或策略的样本内回报与其样本外回报之间的差异。 贝叶斯 SR 也是 pyfolio 的贝叶斯撕样的一部分。
定义自定义概率模型
学生 t 分布相对于低自由度 (DF) 的正态分布表现出肥尾,是捕捉这方面回报的合理选择。因此,我们需要对该分布的三个参数进行建模,即回报的均值和标准差,以及DF。
我们将分别假设均值和标准差的正态分布和均匀分布,以及具有足够低期望值以确保肥尾的 DF 的指数分布。
回报基于这些概率输入,而年化 SR 来自标准计算,忽略无风险利率(使用每日回报)。 我们将提供 2010-2018 年的 AMZN 股票回报作为输入:
mean_prior = data.stock.mean()
std_prior = data.stock.std()
std_low = std_prior / 1000
std_high = std_prior * 1000
with pm.Model() as sharpe_model:
mean = pm.Normal('mean', mu=mean_prior, sd=std_prior)
std = pm.Uniform('std', lower=std_low, upper=std_high)
nu = pm.Exponential('nu_minus_two', 1 / 29, testval=4) + 2
returns = pm.StudentT('returns', nu=nu, mu=mean, sd=std,
observed=data.stock)
sharpe = returns.distribution.mean / returns.distribution.variance **.5 * np.sqrt(252)
pm.Deterministic('sharpe', sharpe)我们在 PyMC3 工作流程的上一节中介绍的板块表示法将三个参数及其关系可视化,以及我们在下图中提供的回报和观察次数然后我们运行我们在上一节中介绍的 MCMC 采样过程。在对四个链中的每一个进行大约 25,000个样本后,我们获得模型参数的后验分布如下,结果显示在下图中:
plot_posterior(data=trace);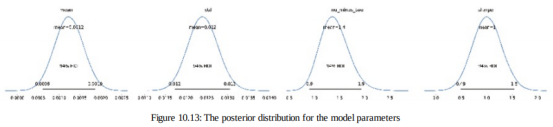
现在我们知道如何评估单个资产或投资组合的 SR,让我们看看如何使用贝叶斯 SR 比较两个不同回报系列的表现。
比较两个回归系列的表现
为了比较两个回报系列的表现,我们将分别对每个组的 SR 进行建模,并将效应大小计算为波动率调整回报之间的差异。对应的概率模型,如下图所示,自然更大,因为它包含两个SR,加上它们的差异:

一旦我们定义了模型,我们就通过 MCMC 采样过程运行它以获得其参数的后验分布。我们使用 2010-2018 年 AMZN 股票的 2,037 日回报,并将其与同期标准普尔 500 指数的回报进行比较。我们可以使用任何策略回测的回报,而不是 AMZN 回报。
可视化跟踪揭示了对每个指标分布的精细性能洞察,如图 10.15 中的各种图表所示:
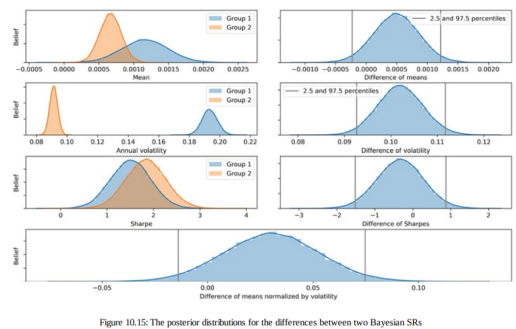
最重要的指标是底部面板中两个 SR 之间的差异。 给定完整的后验分布,从 SR 的角度可以直接直观地可视化或计算一个返回序列优越的概率。
最后
以上就是美好树叶最近收集整理的关于《Machine Learning for Algorithmic Trading》Bayesian ML贝叶斯机器学习 – 动态夏普比率和配对交易用于性能比较的贝叶斯夏普比率的全部内容,更多相关《Machine内容请搜索靠谱客的其他文章。








发表评论 取消回复