说在前面

• 原文地址：OpenAI
• 其它：本文为翻译，最后面还有点小尾巴，之后更新

开始

• 欢迎来到我们的强化学习介绍，这篇文章会涉及以下知识点：
  • 课题中使用到的语言和符号
  • 对强化学习能做什么这个问题进行较高层面的解释
  • 算法中遇到的一些关键数学知识
• 概括来说，强化学习是对智能体(agents)以及他们如何通过试错来学习的研究。它的主要概念是：根据智能体的行为对智能体进行奖励或惩罚，让他在之后的行动中做出合适的行为(在特定场合，提高某些行为的可能性，降低某些行为的可能性)。

强化学习能做什么

• 近来，强化学习在许多领域取得了成功 (有写论文那味了) 。例如，它可以用来让计算机控制仿真机器人；
  

在现实世界中，已有许多著名的例子，例如用于创造用于复杂策略性游戏（围棋、Dota(农药应该也是)）的突破性AI、让计算机直接从像素(图像)中学习如何玩Atari游戏、以及训练仿真机器人来执行人类的命令。

关键概念和术语

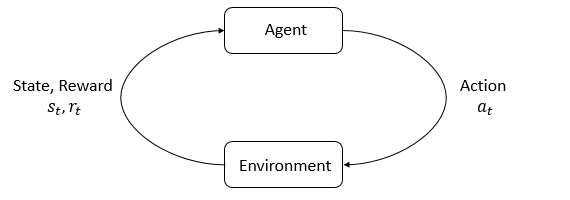
• 强化学习中的关键角色是智能体(agent)和环境(environment)。环境指的是智能体所在的、并且进行交互的世界。在每一个交互步骤中，智能体可以获得对环境当前状态的(部分)观察/认知，然后决定它的下一个行为(action)。环境会因为智能体的行为而改变，它也可以自己进行改变。
• 智能体还会接收到环境反馈的奖励(reward)信号，这个信号的值反映了当前环境的状态是好还是坏。智能体的目标是最大化奖励的累计值，这个累计值被称为return(收益、报酬)。强化学习方法是智能体能够学习行为来达成目标的方式。
• 为了更加具体的理解强化学习，我们需要介绍额外的术语：
  • states and observations(状态和观测值)
  • action spaces(行为空间)
  • policies(策略)
  • trajectories()
  • different formulations of return
  • the RL optimization problem(最优解问题)
  • value functions(值函数)

states and observations

• 状态(state)s是对环境状态的一个完整描述。这个状态对象包含了世界的所有信息。观测结果(observation)o则是对某个状态的部分描述，可能会忽略某些信息。
• 在深度强化学习中，我们通常会用实数向量、矩阵或者高阶张量(real-valued vector, matrix, or higher-order tensor)来表示状态和观测结果。例如，一个视觉上的观测结果可以使用RGB矩阵来表示；机器人的状态可以用关节点的角度和速度来表示。
• 如果智能体可以观测环境的完整状态，我们称这个环境是被全量观测(fully observed)的；如果智能体只能获得一个残缺的观测结果，我们称这个环境是被部分观测(partially observed)的
• 冷知识
  强化学习符号系统(Reinforcement learning notation)有时会将某些更适用于使用observation的地方用state代替。具体来讲，这是在讨论智能体选择行为的时候：在符号系统(notation，这个要怎么翻译啊 )中，我们通常会说行为是取决于状态的；但是在实践中，行为通常是取决于观测结果的，因为智能体是无法直接获得环境的状态的。在我们的教程中，我们遵循符号系统的规则，但是我们应该从上下文来理解状态是指观测结果还是就是状态。

action spaces

• 不同环境允许的行为是不同的。环境中允许的行为集合被称为行为空间(action space)。有些环境拥有离散行为空间(discrete action spaces)，例如Atari和围棋，智能体的合理行为是有限次数的移动。另一些环境拥有连续行为空间(continuous action spaces)，例如在真实世界中控制机器人的智能体。在连续行为空间中，行为通常是实数向量。
• 上述区别对深度强化学习中的方法有着深刻的影响。某些算法可能可以直接应用于其中一种环境(以上述两种行为空间分类)，但是想要应用于另一种环境，就必须重写算法。

policies

• 策略是智能体决定行为的规则。
  策略可以是确定性(deterministic)的，通常用$\mu$表示：
  $$a_t=\mu (s_t)$$
  策略也可以是随机性(stochastic)的，通常用$\pi$表示：
  $$a_t\sim \pi (\cdot |s_t)$$
  由于策略本质上是智能体的大脑，用“策略”一词来代替“智能体”是罕见的，例如说“策略偏向于最大化奖励”。
• 在深度强化学习中，有参数化策略(parameterized policies)一词：策略的输出是依赖于一组参数(例如神经网络的weights和biases)，我们可以通过一些优化算法来调整这些参数来改变行为(应该是类似RNN那种？)。
  我们通常用$\theta$或$\varphi$来表示这种策略的参数：
  $$\begin{gathered} a_t={\mu }_{\theta }(s_t) \\ {a}_t\sim {\pi }_{\theta }(\cdot |s_t) \end{gathered}$$

deterministic policies

• 下面是在pytorch中构建一个用于连续性行为空间(continuous action space)的简单确定性策略的代码片段：

  pi_net = nn.Sequential(
  nn.Linear(obs_dim, 64),
  nn.Tanh(),
  nn.Linear(64, 64),
  nn.Tanh(),
  nn.Linear(64, act_dim)
  )
  

  上述代码构造了一个拥有两个隐层以及激活函数tanh的多层感知器网络(MLP)。假设obs是包含一个batch观测结果(observation)的Numpy数组，那么执行pi_net可以得到一个batch的行为(action)：

  obs_tensor = torch.as_tensor(obs, dtype=torch.float32)
  actions = pi_net(obs_tensor)
  

stochastic policies

• 深度强化学习中的两种常用随机性策略是：categorical policies以及diagonal Gaussian policies。
• categorical policies可用于离散行为空间；diagonal Gaussian policies可用于连续行为空间。
• 以下两个计算方法对于随机性策略是十分重要的：
  • 对行为采样
  • 计算对数似然估计
• 两种随机性策略详细介绍(这个翻译不动啊)

trajectories

• 轨迹(trajectory)$\tau$是环境中的状态和行为的序列：
  $$\tau =(s_0,a_0,s_1,s_1,...)$$
• 环境中的第一个状态，$s_0$，是从start-state distribution(启动状态分布)中随机选取的，有时用${\rho }_0$表示：
  $$s_0\sim {\rho }_0(\cdot )$$
  (表示$s_0$遵循一个随机分布)
• 状态转换，即环境从时间点$t$的状态$s_t$到时间点$t+1$的状态$s_{t+1}$的变化，只取决于环境本身的规则以及离时间点$t$最近的行为$a_t$：
  $$\begin{gathered} s_{t+1}=f(s_t,a_t)(确定性) \\ {s}_{t+1}\sim P(\cdot |s_t,a_t)(随机性) \end{gathered}$$
  (前一个公式好理解；后一个表示$s_{t+1}$遵循一个随机分布，并且该状态是在状态$s_t$下执行行为$a_t$后产生的)
  而行为取决于智能体的策略

different formulations of return

• 奖励函数$R$在强化学习中是非常重要的。它与环境的当前状态、当前时间点采取的行为以及环境的下一个状态有关：
  $$r_t=R(s_t,a_t,s_{t+1})$$
  上述公式也时常被简化成只取决于当前状态的形式：
  $$r_t=R(s_t)$$
  或者当前状态-当前行为对的形式：
  $$r_t=R(s_t,a_t)$$
• 智能体的目标是最大化环境轨迹(trajectory)上的累计奖励，但是这个概念是有些意义的。我们用$R(\tau )$来表示这个概念。
  • 一种return是finite-horizon undiscounted return，它仅仅是一段轨迹(序列)的累计和：
    $$R(\tau )=\sum _{t=0}^{\infty }{r}_t$$
  • 另一种return是infinite-horizon discounted return，它包含了智能体获得的所有奖励，但是会随着时间衰减，衰减系数为$\gamma \in (0,1)$：
    $$R(\tau )=\sum _{t=0}^{\infty }{\gamma }^t{r}_t$$
    为什么需要衰减系数呢？我们不是就是需要所有奖励的累计和吗？确实，但是衰减系数既直观(cash now is better than cash later，这啥意思？)，还有一定的数学意义$($无限制的直接对奖励值进行累加可能不会得到一个有穷值(可能无穷大)，并且难以进行等值比较(两个无穷值)，使用衰减可以解决上述问题$)$。

the RL optimization problem

• 无论选择那种return方式、策略，强化学习的目标都是选择一个在依照策略行动后能够最大期望return值的策略。
• 在讨论期望回报之前，我们需要了解轨迹上的概率分布。假定环境变换和策略都是随机的，那么时间$T$内的概率为：
  $$P(\tau |\pi )={\rho }_0(s_0)\prod _{t=0}^{T-1}P(s_{t+1}|s_t,a_t)\pi (a_t|s_t)$$
  (这个公式展开其实大致是轨迹$\tau$的产生过程，即$s_0,a_0,s_1,a_1,...$，$P$是在状态$s_t$下执行$a_t$产生$s_{t+1}$的概率，$\pi$是在状态$s_t$下执行$a_t$)
• 期望回报为：
  $$J(\pi )=\int (P(\tau |\pi ))R(\tau )=E_{\tau \sim \pi }[R(\tau )]$$
  (积分，概率*回报=期望回报)
• 优化问题为：
  $${\pi }^{\ast }=\arg \underset{\pi }{\max }J(\pi )$$

value functions

• 获取环境状态或者状态-行为对的值是十分有用的。使用数值，我们可以估计某一状态或状态-行为对的期望回报，然后依照某个特定策略行动。几乎每一个强化学习算法中都有值函数。
• 以下介绍四个主要的值函数：
  • On-Policy Value Function
    开始于状态$s$，之后的每一个行为都通过策略$\pi$来决定
    $$V^{\pi }(s)=E_{\tau \sim \pi }[R(\tau )|s_0=s]$$
  • On-Policy Action-Value Function
    开始于状态$s$，并采取任意一个行为(可以不是来自策略$\pi$的)，之后的每一个行为都通过策略$\pi$来决定
    $$Q^{\pi }(s,a)=E_{\tau \sim \pi }[R(\tau )|s_0=s,a_0=a]$$
  • Optimal Value Function
    开始于状态$s$，之后的每一个行为都通过优化后的策略$\pi$来决定
    $$V^{\ast }(s)=\underset{\pi }{\max }{E}_{\tau \sim \pi }[R(\tau )|s_0=s]$$
  • Optimal Action-Value Function
    开始于状态$s$，并采取任意一个行为(可以不是来自策略$\pi$的)，之后的每一个行为都通过优化后的策略$\pi$来决定
    $$Q^{\ast }(s,a)=\underset{\pi }{\max }{E}_{\tau \sim \pi }[R(\tau )|s_0=s,a_0=a]$$

The Optimal Q-Function and the Optimal Action

• 在optimal action-value function$Q^{\ast }(s,a)$与依照优化策略采取的行为之间有着重要的联系。$Q^{\ast }(s,a)$的定义见上文。
• 优化策略会选择任意一个能够在状态$s$时最大化回报的行为。因此，如果我们有$Q^{\ast }$，那么我们可以直接得到最优的行为，以$a^{\ast }(s)$表示：
  $$a^{\ast }(s)=\arg \underset{a}{\max }{Q}^{\ast }(s,a)$$
• 注意：$Q^{\ast }(s,a)$可能有多个最优解，优化策略可以从这些最优解中随机选择一个。但是总是会有一个最优策略来决定选择哪一个行为。

Bellman Equations

• 上述四个值函数都遵循一个特别的自我一致性等式，称为贝尔曼等式。它的主要思想是：起始点的值，等于你到达起始点的期望回报+执行下一步动作的回报
• 对于on-policy value functions(前两种值函数)，贝尔曼等式为：
  $$\begin{gathered} V^{\pi }(s)=\underset{s^{\prime }\sim P}{\underset{a\sim \pi }{E}}[r(s,a)+\gamma V^{\pi }(s^{\prime })] \\ {Q}^{\pi }(s,a)=\underset{s^{\prime }\sim P}{E}[r(s,a)+\gamma \underset{a^{\prime }\sim \pi }{E}[Q^{\pi }(s^{\prime },a^{\prime })]] \end{gathered}$$
  其中$s^{\prime }\sim P$代表$s^{\prime }\sim P(\cdot |s,a)$，表示下一个状态$s^{\prime }$是根据环境的变换规则产生的；$a\sim \pi$ 代表$s\sim \pi (\cdot |s)$；$a^{\prime }\sim \pi$代表$a^{\prime }\sim \pi (\cdot |s^{\prime })$。
• 对于optimal value functions，贝尔曼等式为：
  $$\begin{gathered} V^{\ast }(s)=\underset{a}{\max }\underset{s^{\prime }\sim P}{E}[r(s,a)+\gamma V^{\ast }(s^{\prime })] \\ {Q}^{\ast }(s,a)=\underset{s^{\prime }\sim P}{E}[r(s,a)+\gamma \underset{a^{\prime }}{\max }{Q}^{\ast }(s^{\prime },a^{\prime })] \end{gathered}$$
• 上述两种等式之间最主要的差异是：行为是否是最优解。它反映的事实是：无论智能体何时去选择行为，为了行动的最优化，它必须选择能够带来最高收益的行为。

Advantage Functions

• 在强化学习中，有时我们并不关心行为的绝对优势，只需要知道在某个状态下这个行为比其他行为好即可。也就是说，我们想要知道行为的相对优势。
• 优势函数$A^{\pi }(s,a)$描述了在状态$s$时采取行为$a$所获得的期望回报相对于在状态$s$随机选择行为所获得的期望回报的好坏程度；公式如下：
  $$A^{\pi }(s,a)=Q^{\pi }(s,a)-V^{\pi }(s)$$
  （对比$Q^{\pi }(s,a)$和$V^{\pi }(s)$的定义可以很好的理解这个公式，$\pi$是随机选择行为的策略，$Q$是第一次选择一个指定的行为，之后都按$\pi$选择；$V$是一直按$\pi$选择）

最后

以上就是魔幻大侠为你收集整理的【强化学习/OpenAI】强化学习中的关键概念说在前面开始强化学习能做什么关键概念和术语的全部内容，希望文章能够帮你解决【强化学习/OpenAI】强化学习中的关键概念说在前面开始强化学习能做什么关键概念和术语所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。