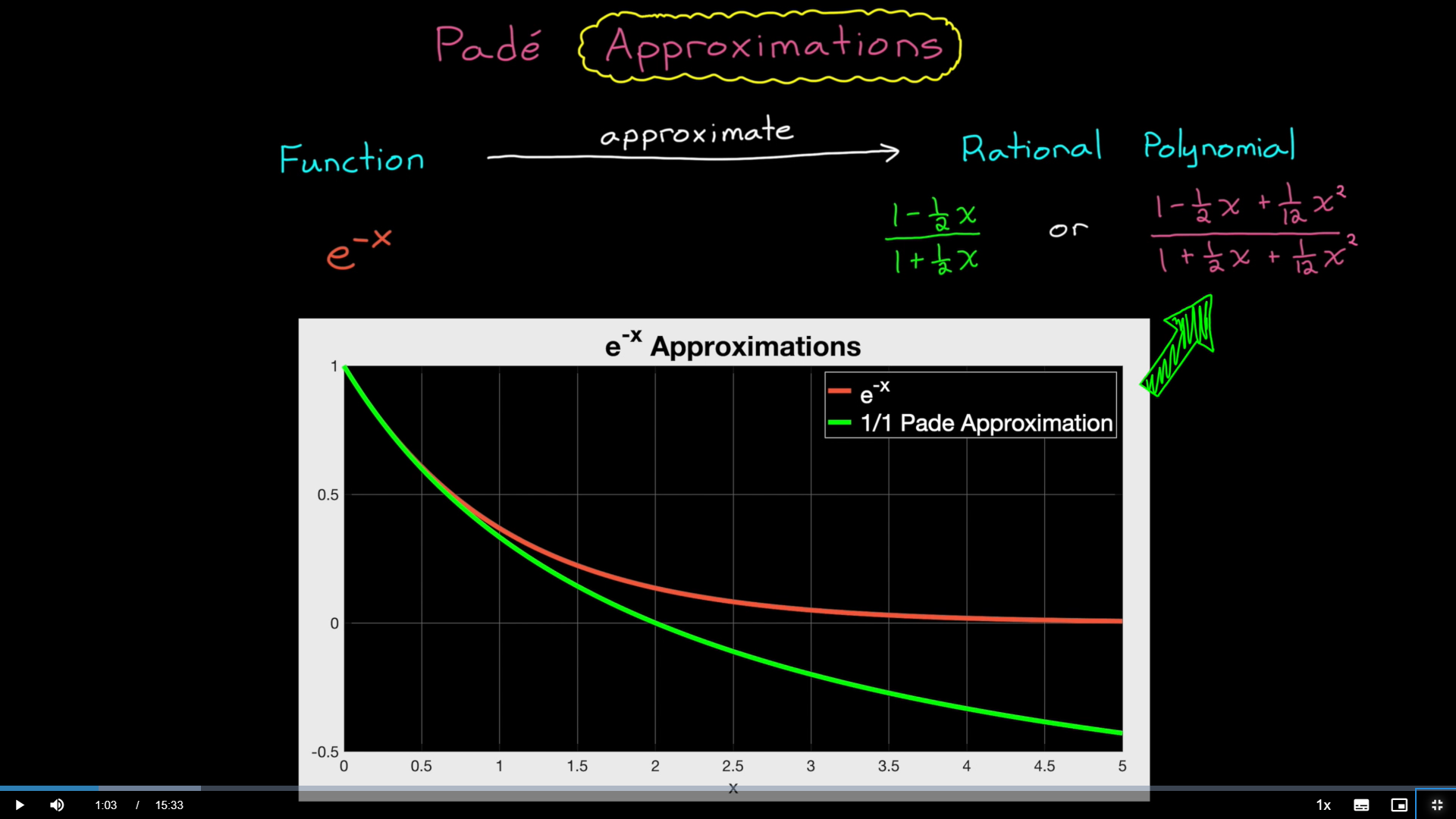
1 pade approximations是什么？

Padé Approximations是一种对pure delay使用常规传函进行近似替换的方法，matlab提供了的一个库函数pade。
在传递函数中，用$e^{-\tau s}$表示纯延时pure delay环节，它对信号的幅值不会有任何影响，只会影响信号的相位。

2 为什么需要进行近似？

1）不能进行根轨迹分析
因为$e^{-\tau s}$并不包含零极点，如果进行根轨迹rlocus分析，pure delay环节的影响并不能得到体现，但是它对控制系统的影响却非常的大。
2）影响LQR和H∞控制器设计

具体原因不在这里展开。

3 如何计算？

传递函数的一般表达式如下，m和n分别表示分子和分母的阶次。

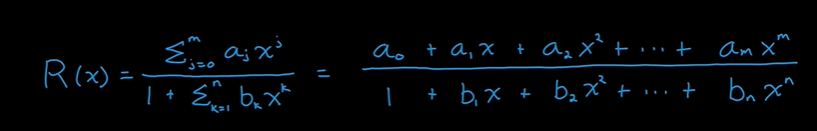
使用泰勒级数展开。

以m = n = 1为例，进行计算。

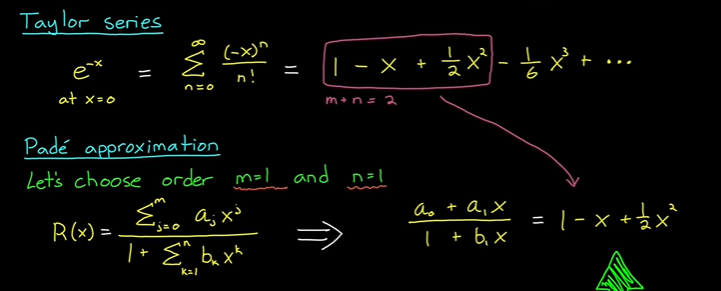
然后把等式展开，求取各项系数。

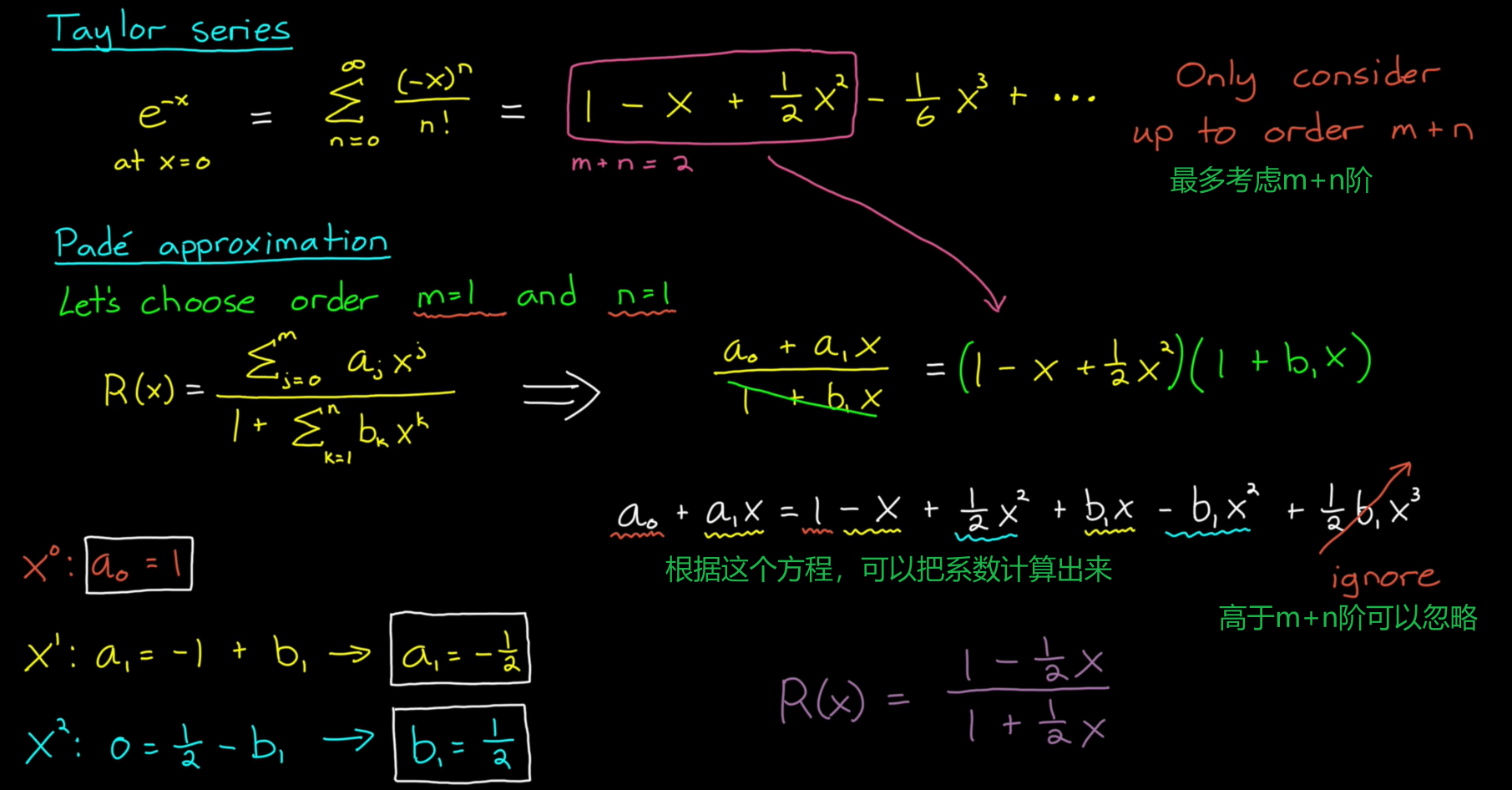
当m、n取不同的值时，其近似的传函如下表。那我们究竟该如何选择呢？带着这个问题，看下一章节。

4 两个重要的问题

先回答第2个问题，这个问题相对比较容易回答。
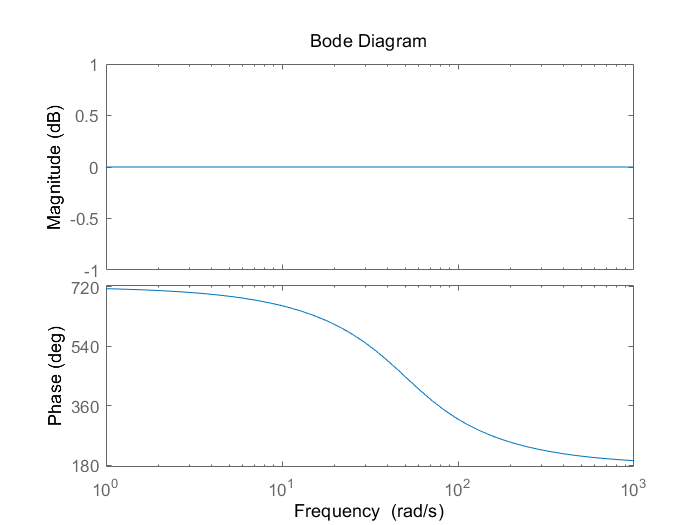
仅仅只有当m=n时，近似的传函的增益始终为1，也就是0dB，也就不会对信号幅值进行放大或者缩小，这是我们所期望的。至于为什么，大家可以看上面的m、n取不同值时近似传函的表格。
下面是一个例子，根据bode图可以看出，其幅值一直都是0dB。

再回答第1个问题。大家都知道，如果泰勒级数的阶数越高，越能更精确的近似$e^{-s}$。
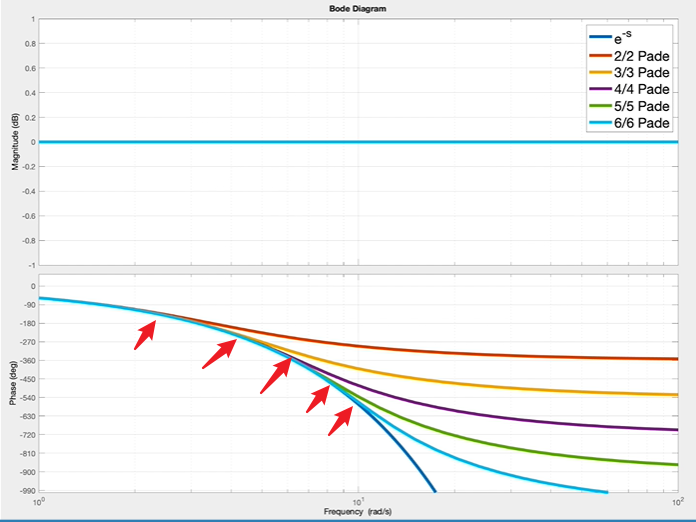
下图中，绘制了不同阶数传函与$e^{-s}$的bode图，可以看出，阶数越高，相位出现“偏离”时对应的频率也越高，也就是能覆盖更高的频率范围。

那么阶次的选择依据如下：
出现相位”偏离“对应的频率要大于 -3dB 对应的截止频率(cutoff frequency)，如下图所示。

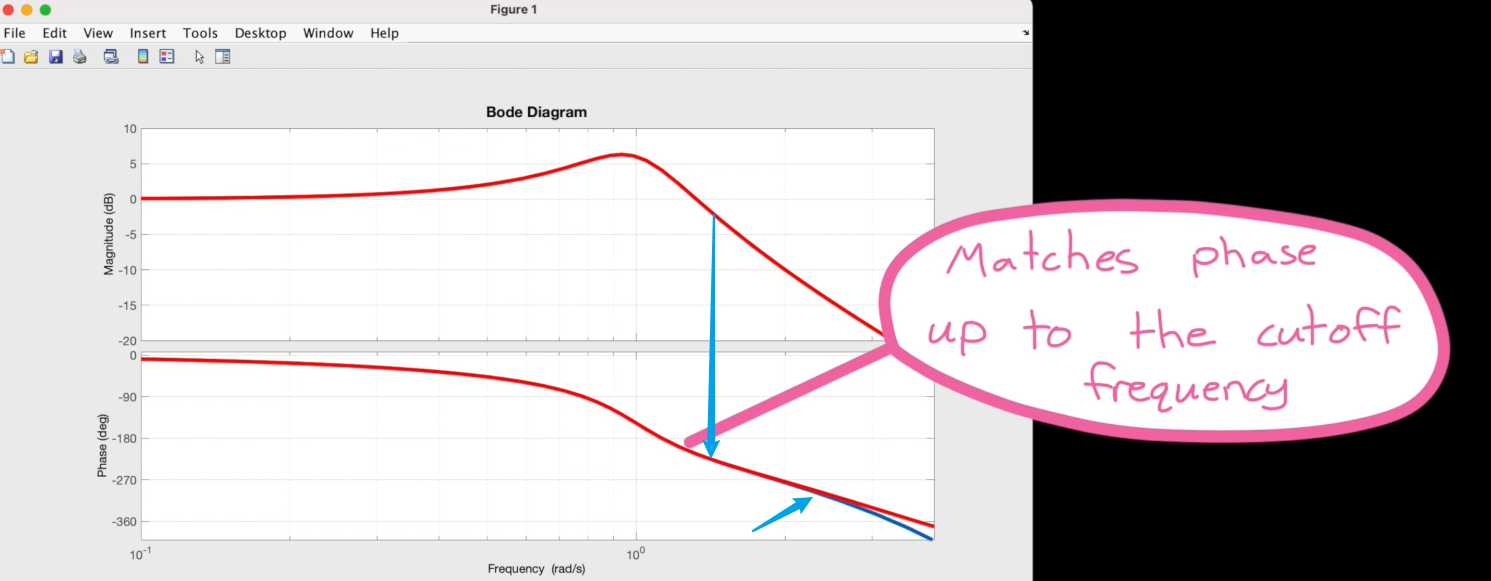
这个很好理解，在我们关心的频率范围内，尽量不要有太大的相位误差。

5 参考

本文仅仅是对下面视频的笔记，如要了解更详细的信息，可以查看下面的链接。
https://ww2.mathworks.cn/videos/control-systems-in-practice-part-12-why-pade-approximations-are-great-1655105423132.html

最后

以上就是刻苦面包为你收集整理的【笔记】Pade Approximations1 pade approximations是什么？2 为什么需要进行近似？3 如何计算？4 两个重要的问题5 参考的全部内容，希望文章能够帮你解决【笔记】Pade Approximations1 pade approximations是什么？2 为什么需要进行近似？3 如何计算？4 两个重要的问题5 参考所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。