一、软件性能获取

分别使用 Matlab 工具和C++语言获得计算下列算法的最大时间，最小时间及平均时间,以及相应的软件功耗：

1.1 一维数组排序

数组选择一万个，使用快速排序。处理器为英特尔i5-7200U，2.5GHz，热设计功耗为15W，Matlab版本为2021a，gcc版本为6.3.0。

1.1.1 Matlab

Quic.m

function [A,index]=quic(A,i,j)
key=A(i);
while i<j
while i<j&&A(j)>=key
j=j-1;
end
if i<j
A(i)=A(j);
end
while i<j&&A(i)<=key
i=i+1;
end
if i<j
A(j)=A(i);
end
end
A(i)=key;
index=i;
end

quicsort.m

function A=quicsort(A,low,high)
if low<high
[A,key]=quic(A,low,high);
A=quicsort(A,low,key-1);
A=quicsort(A,key+1,high);
end
end

test.m

a = [];
%自动生成的一万个数据
n = length(a);
t=[0,0,0,0,0,0,0,0,0,0];
for i = 1:10
b = a
tic
A = quicsort(b,1,n)
t(i) = toc
end
disp("max=")
disp(max(t))
disp("min=")
disp(min(t))
disp("mean=")
disp(mean(t))
t

使用的微处理器为 Intel®i5-7200U@2.5GHZ，其热设计功耗为 15w，其 10% 为 1.5w。这样这个程序最小、最大、平均能耗分别为：0.0648w、0.1591w、0.084w。

1.1.2 C++

#include<iostream>
#include <iomanip>
#include<memory.h>
using namespace std;
int *partition(int *arr,int L,int R);
void swap(int *arr,int a,int b)
{
int tmp=arr[a];
arr[a]=arr[b];
arr[b]=tmp;
}
void quick_sort(int *arr,int L,int R)
//主函数中调用的函数，参数仍为	
{
数组、左边界下标、右边界下标
if(L<R){
int *p=partition(arr,L,R);
//之前函数的返回值，也就是我们分
割数组三部分的边界线 
quick_sort(arr,L,p[0]-1);
//对小于区进行快排 
quick_sort(arr,p[0+1],R);
//对大于区进行快排 
}
}
int *partition(int *arr,int L,int R)
//数组、左边界下标、右边界下标 
{
int little_border=L-1;
//小于区右边界 
int big_boder=R;
//大于区左边界 
while(L<big_boder)
//从头遍历到尾 
{
if(arr[L]<arr[R])
//当前数比选定数小 
swap(arr,++little_border,L++);
//放在小于区里面，小于区范围++，
进入下一个数 
else if(arr[L]>arr[R])
//当前数比选定数大
swap(arr,--big_boder,L);
//放在大于区里面，大于区范围++，
停在当前位置 
else
L++;
//放着不动，相当于等于区，进入下
一个数 
}
swap(arr,big_boder,R);
//最后把选定的数放在等于区 
int *res=(int *)malloc(sizeof(int)*2);
//最后返回一个数组
res[0]=little_border+1;
//数组成员有等于区的左边界 
res[1]=big_boder;
//还有等于区的右边界 
return res;
//函数返回这个数组的指针，方便我
们进行下一次的递归快排 
}
int main()
{
int arr_origin[10005] = {……}
//自动一万个数字，此处太多，就
不放了
int len=10000;
int arr[10005];
double clockstart, clockend;
int time[10] = {0};
int Max,Min,Ave,sum;
int times = 0;
Max = -1;
Min = 10000;
Ave = 0;
sum = 0;
while(times != 10)
//执行十次
{
memcpy(arr,arr_origin, sizeof(int) * 10000);
//数组重新赋值
clockstart = clock();
quick_sort(arr,0,len-1);
clockend = clock();
time[times] = clockend - clockstart;
times++;
}
//计算最大最小 平均耗时
for(int i = 0;i < 10;i++)
{
int x = time[i];
if (x > Max)
Max = x;
if (x < Min)
Min = x;
sum += x;
cout<<time[i] <<" ";
}
Ave = sum / 10;
cout<< "n Max"<<Max<<"
Min:"<<Min <<"
Ave:"<<Ave<<endl;
return 0;
}

运行了十次，可以看到最大的执行时间为5ms，最小的为2ms，平均执行时间为3ms。

使用的微处理器为 Intel®i5-7200U@2.5GHZ，其热设计功耗为 15w，其 10% 为 1.5w。这样这个程序最小、最大、平均能耗分别为：0.003w、0.0075w、0.0045w。

1.2 实现 1+2+3+………+10000000的求和

1.2.1 Matlab

t=[0,0,0,0,0,0,0,0,0,0];
for i = 1:10
sum = 0;
tic
for j = 1:10000000
sum =
sum + j;
end
t(i) = toc;
sum
end
disp("max=")
disp(max(t))
disp("min=")
disp(min(t))
disp("mean=")
disp(mean(t))
t

使用的微处理器为 Intel®i5-7200U@2.5GHZ，其热设计功耗为 15w，其 10% 为 1.5w。这样这个程序最小、最大、平均能耗分别为：0.021w、0.0315w、0.024w。

1.2.2 C++

#include<iostream>
#include<time.h>
using namespace std;
long long int add(long int input)
{
long long int sum = 0;
for(int i = 1; i <= input; i++)
sum += i;
return sum;
}
int main()
{
int n = 10000000;
long long int result = 0;
double clockstart, clockend;
clockstart = clock();
result = add(n);
clockend = clock();
cout<<clockend - clockstart<<endl;
cout<<result;
return 0;
}

使用的微处理器为 Intel®i5-7200U@2.5GHZ，其热设计功耗为 15w，其 10% 为 1.5w。这样这个程序最小、最大、平均能耗分别为：0.0315w、0.036w、0.033w。

1.3 实现1000的阶乘

使用数组模拟，数组的每一位代表结果的每一位。数组的长度为结果的长度。

#include <iostream>
#include<time.h>
using namespace std;
int main()
{
int k=1;
//k为当前的位数
int fact[10000]={1,0};
int n=1000;
double clockstart, clockend;
clockstart = clock();
for(int i = 1; i <= n; i++)
{
for(int j = 0; j < k; j++)
{
fact[j] = i * fact[j];
//各位乘
}
for(int j = 0; j < k; j++)
{
if(fact[j] >= 10)
{
fact[j+1] += fact[j] / 10;
fact[j] = fact[j] % 10;
}
}
while(fact[k]>=10)
//先看大于等于10的
{
fact[k+1] += fact[k] / 10;
fact[k] = fact[k] %10;
k++;
}
if(fact[k] > 0)
//只剩下大于0小于10的，这最高一位了
{
k++;
//结束之后,k比最高位下标多了 1
}
}
clockend = clock();
cout<<clockend - clockstart<<endl;
for(int j=k-1; j>=0;j--)
{
cout<<fact[j];
}
return 0;
}

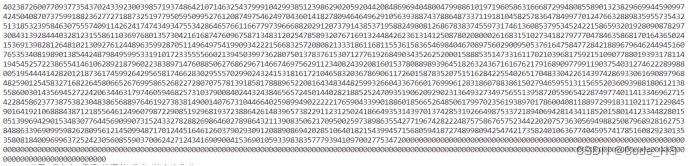
阶乘计算部分耗时12ms，计算结果如下，共有2568位。

二、通信时延

设通信总量N为10000字节，总线宽度W为32位，一次传输一个字节需要8位，每次总线时长即访问周期TB为20ns，计算完成这个通信量传输所需要的时延。若通信总量N为9981字节，其他相同，问完成这个通信量传输需要多长时间？

解：
32位=4字节, 向上取整
T1 = 10000/420 = 50000ns
T2 = 9981/420 = 49920ns

最后

以上就是机智芒果为你收集整理的快速排序、求和、模拟阶乘并利用vscode c++和matlab对程序进行计时一、软件性能获取二、通信时延的全部内容，希望文章能够帮你解决快速排序、求和、模拟阶乘并利用vscode c++和matlab对程序进行计时一、软件性能获取二、通信时延所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。