摘要
本篇为自学matlab笔记,主要参考书为《matlab r2016a完全自学一本通》
如有侵权烦请告知删除
第一章 2016a概述
| 命令 | 命令说明 |
|---|---|
| cd | 显示或改变当前工作文件夹 |
| dir | 显示当前文件夹或指定目录下的文件 |
| home | 将光标移到命令行窗口的最左上角 |
| clf | 清除图形窗口 |
| type | 显示文件内容 |
| echo | 工作窗信息显示开关 |
| disp | 显示变量或文字内容 |
| load | 加载指定文件的变量 |
| diary | 日志文件命令(将命令行窗口文本记录到日志文件中) |
| ! | 调用DOS命令 |
| exit 或 qiut | 退出matlab |
| pack | 收集内存碎片 |
| hold | 图形保持开关 |
| path | 显示搜索目录 |
| save | 保存内存变量到指定文件 |
echo说明:
echo 指令— 用来控制m文件在执行过程中是否
显示
echo on — 打开所有命令文件的显示方式
echo off — 关闭所有命令文件的显示方式
echo — 在以上两者间切换
echo对于命令文件函数文件有所不同,命令文件用法简单,函数对所有命令起作用;函数文件用法较复杂,具体请help查询。
echo file on — 打开file函数文件的显示方式
echo file off — 关闭file函数文件的显示方式
echo file — 切换file函数文件的显示方式
echo on all — 打开所有函数文件的显示方式
echo off all —关闭所有函数文件的显示方式
第二章 matlab基础知识
1.1.1 取整函数
| 函数名称 | 功能说明 |
|---|---|
| floor | 向下取整 |
| ecil | 向上取整 |
| round | 取最接近的整数,如果小数部分是0.5,则向绝对值大的方向取整 |
| fix | 向0取整 |
八种内置整形数据类型
int8 uint8 int16 uint16 iny32 uint32 int64 uint64
1.2 浮点数类型
| 浮点类型 | 储存位宽 | 转换函数 |
|---|---|---|
| 单精度 | 32 | single |
| 双精度 | 64 | double |
注意:整数只能与同类整数或标量双精度相乘
int8 类型整数 只能与 int8类型或double相乘
1.3 复数
matlab中默认使用i和j作为虚部的标志,创建虚数可以按照复数形式直接输入也可以使用complax函数
关于复数的相关函数
| 函数名称 | 功能 | 函数名称 | 功能 |
|---|---|---|---|
| real(z) | 返回实部 | imag(z) | 返回虚部 |
| abs(z) | 返回z的模 | angle(z) | 返回z的辐角 |
| conj(z) | 返回z的共轭复数 | comlex(a,b) | 以a为实部,b为虚部创建复数 |
1.4 无穷量 和 非数值量
Inf NaN
非数值量是由于 0/0 或 Inf/Inf 类型的非正常运算产生的
2.1.2 逻辑类型
< <=
> >=
==
~=
逻辑运算符
& | ~
与 或 非
2.1.3 字符和字符串
字符串的单引号是用两个连续的单引号表示的
字符串也有切片操作
字符串的连接可以直接将字符串数组连接实现
U = 'hello ';
V = ' world';
W = [U V]
W = U+V
输出结果:
W =
hello world
W =
136 220 219 222 219 132
可见连接两个字符串的操作是 [ ]
2.1.4 函数句柄
对函数调用有直接调用和间接调用两种方法
创建函数句柄
function_handle =@function_name;
其中function_name是函数所对应的M文件的名称或Mtalab内部函数名称
@ 是句柄创建操作符
function_handle 变量保存函数句柄
函数句柄的操作函数
| 函数名称 | 函数功能 |
|---|---|
| functions(funhandle) | 返回一个结构体,储存了函数的名称、函数类型以及函数.M文件的位置 |
| func2str(funhandle) | 将函数句柄转换为函数名称的字符串 |
| str2func(str) | 与像一个相反 |
等
2.1.5 结构体类型
创建结构体的两种方法:
1、
student.name = 'caiji';
student.age = 22;
student.grade = 2;
student
输出:
student =
name: 'caiji'
age: 22
grade: 2
2、利用struct函数创建结构体
student = struct('name','caiji','age',22,'grade',2)
结果同上
2.1.6 数组类型
[ ]
:
类似于python的列表操作
2.1.7 单元数组类型
元胞数组 cell
对于单元数组C,C(m,n)指的是单元数组中第m行第n列的单元,而C{m,n}指的是单元数组中第m行第n列单元中的内容
一个是“单元数组”一个是“单元中的内容”
单元数组的合并 a,b都是元胞 c = {a,b}
单元数组中指定数组的删除
如果要删除单元数组中指定的某个单元,只需要将空矩阵赋值给该单元即可
c{m,n} = []
删除后改位置元素会是一个空数组
要删除元胞中的单元的话,使用小括号
c(m) = []
使用 reshape 改变单元数组的形状
将c改变为一个m行n列的形状
b = reshape(c,m,n)
2.1.8 map容器类型
map类似于python中的字典,有key和value
一个map是matlab中的对象,有以下属性
| 属性 | 说明 | 默认值 |
|---|---|---|
| Count | uint64,表示在map中存的key总数 | 0 |
| KeyType | 字符串,表示key类型 | char |
| ValyeType | 字符串表示value类型 | any |
map中属性查看方法为map名+小数点”.“+map的属性名
创建map对象:
通过构造函数创建map
map_obj = containers.Map({'k1','k2','k3'},{'v1','v2','v3'})
结果如下:
map_obj =
Map (具有属性):
Count: 3
KeyType: char
ValueType: char
查看读取map对象
keys(map_obj)
values(map_obj)
结果如下:
ans =
‘k1’ ‘k2’ ‘k3’
ans =
‘v1’ ‘v2’ ‘v3’
读取map对象
在创建好一个map对象后,用户可以对其进行数据寻访,寻访指定键所对应的值
val = map_obj('k2')
结果如下:
val =
v2
编辑map对象
1、删
remove(map_obj,'k1')
2、增
map_obj('k6') = '233'
3、改
map_obj('k6') = '23366'
2.2 基本矩阵操作
向量:当m=1或n=1时,建立的矩阵成为向量
标量:当m=n=1 时建立的矩阵成为标量
单个实数或复数在matlab中都是以矩阵形式储存的,在matlab中,单个数据或单个数据构造的矩阵都是标量
空矩阵:当m=n=0或m=0或n=0,创建的矩阵成为空矩阵
对矩阵的操作有旋转、改变维度、排序、逆序等,函数挺多,用的时候再记
对二维数组元素的索引有双下标索引和单下标索引
单下标索引遵循列优先原则
线性引用矩阵元素:
矩阵中某一元素的单下标索引和双下标索引之间,可以通过matlab内部函数进行转换:
IND = sub2ind(siz,i,j)
功能为将双下标索引值转换为单下标索引,其中 siz 是一个包含两个元素的数组,代表了转换矩阵的行列数,一般可以用 **size(A)**表示,i,j分别表示双下标索引中的行列值,IND是转换后单下标索引值
反之:单下标转双下标
[I,J] = ind2sub(siz,ind)
tips: 求和函数 sum()
matlab中还提供一个关键字end,用于表示该维中的最后一个元素
2.2.5 矩阵信息的获取
矩阵结构是指矩阵子元素的排列方式
matlab提供了各种测试函数,eg:
isempty(A) 检测矩阵是否为空
isscalar(A) 检测矩阵是否是单元素的标量矩阵
isvector(A) 检测矩阵是否是只具有一行或一列元素的一维向量
issparse(A) 检测数组是否是稀疏矩阵
矩阵大小:
矩阵形状查询函数
| 函数 | 描述 |
|---|---|
| ndims | 获取矩阵的维数 |
| size | 获取矩阵在各维上的长度 |
| length | 获取矩阵在最长维的长度 |
| numel | 获取矩阵元素的个数 |
numel 是number of elements的缩写
矩阵维度:
对于空矩阵、标量矩阵、一维矩阵和二维矩阵,matlab都将其作为普通二维数组对待。用 [] 产生的空矩阵是作为二维矩阵的
矩阵占用内存:
使用whos命令查看当前工作区中指定变量的所有信息
2.2.6 矩阵的保存和加载
矩阵元素的寻址:
1):矩阵下标寻址方法
1、单元素的寻访
A(m,n)
2、矩阵元素区域的寻访
A(1:m,n) 访问第n列的第一个至第m个元素
2)线性寻址
线性寻址的下标是通过矩阵的双下标换算的得来的
A(m,n)
A(i,j) = A((j-1)*m+i)
matlab提供了多个矩阵合并的函数
cat()
horzcat()
vertcat()
repmat()
等
2.3 运算符
+ - * /
.* ./ .^
注意乘和点乘的区别
乘就是矩阵相乘
点乘是对应元素相乘
matlab还提供了大量的运算函数
在此就不进行列表,用的多了自然就熟了
exp(x) 求以e为底数的x次幂
log(x)
log10(x)
sqrt(x) x的平方根
sin(x)
cos(x)
tan(x)
asin(x) 反正弦
acos(x)
atan(x)
mod(a,b) a,b相除余数
min(a,b)
max(a,b)
mean(x) 均值
median(x) 中位数
sum(x)
prod(x) 阵列x的连乘值
cumsum(x) 累积总和值
cumprod(x) 累积连乘值
sign(x)
rem(x,y) x/y 余数
diff(x) x向量的差分
sort(x) 排序
fft(x) 离散傅里叶变换
rank(x) x矩阵的秩
2.3.2 关系运算符
< <=
> >=
==
~=
matlab中重要的逻辑函数:
| 函数名 | 运算法则 |
|---|---|
| xor(x,y) | 异或运算 |
| any(x) | 如果在一个向量中,有任何元素时非0,返回1,否则返回0 |
| all | 全1才是1 ,有0返回0 |
2.4字符串处理函数
matlab字符串处理函数
| 字符串函数 | 函数功能 |
|---|---|
| eval(string) | 作为一个matlab命令求字符串的值 |
| blanks(n) | 返回一个n个0或空格的字符串 |
| deblank | 去掉字符串后拖的空格 |
| feavl | 求字符串给定的函数值* |
| findstr | 从一个字符串内找另一个字符串 |
| isletter | 字母存在时返回真值 |
| isspace | 空格存在时返回真值 |
| Isstr | 输入字符串,返回真值 |
| iasterr | 返回上一个产生matlab错误的字符串 |
| strcmp | 字符串相同,返回真值 |
| strrep | 用一个字符串替换另一个字符串 |
| strtok | 在字符串里找出第一个标记 |
feavl函数:
语法
[y1,…,yN] = feval(fun,x1,…,xM)
说明
示例
[y1,…,yN] = feval(fun,x1,…,xM) 使用函数的名称或其句柄以及输入参数 x1,…,xM 来计算函数的结果。
feval 函数遵循与直接调用函数句柄相同的作用域和优先级规则。有关详细信息,请参阅创建函数句柄。
Isstr函数:
不推荐使用 isstr。请改用 ischar。
2.4.1 字符串的构造
字符串内容要在单引号内,如果字符串内的字符包含单引号,则用两个重复的单引号表示
构造多行字符串时,若字符串内容写在 [ ] 内,那么多行字符串的长度必须相同,若字符串写在{}内,则多行字符串内容可以不同
matlab还提供纵向连接字符串的而函数
strvcat :连接多行字符串时,每行字符串长度不要求相等,所有非最长字符串的右边会自动补偿空格,使每行字符串长度相等
char:与strvcat类似,不过多行字符串有空字符串时,strvcat会直接忽略,char会补偿后再进行连接
2.4.4 字符串数值转换
数据类型转换函数
| 函数名称 | 函数功能 |
|---|---|
| abs | 字符串转ASCII |
| dec2hex | 十进制转十六进制 |
| fprintf | 把格式化的文本写到文件或显示屏上 |
| hex2dec | 十六进制转十进制 |
| int2str | 整形转字符串 |
| lower | 字符串转小写 |
| num2str | 数字转字符串 |
| setstr | ASCII转字符串 |
| sprintf | 用格式控制数字转换字符串 |
| sscanf | 用格式控制数字转换数字 |
| str2mat | 字符串转文本矩阵 |
| str2num | 字符串转数字 |
| upper | 字符串转大写 |
第三章 数组与矩阵
3.1.1数组的创建
访问数组第三个到最后一个元素
a=c(3:end)
数组元素反向输出
a=c(end:-1:1)
通过冒号创建一维数组
x=A:step:B
通过logspace函数创建一维数组
y=logspace(a,b) 该函数创建行向量y,第一个元素为 10a ,最后一个元素为10b,形成总数50个元素的等比数列
y=logspace(a,b,n) 形成总数为n的等比数列
通过linspace创建一维数组
y=linspace(a,b) 创建行向量y,第一个元素为a,最后一个为b
形成总数为100个元素的线性间隔向量
y=linspace(a,b,n) 形成总数为n
3.1.2 数组常见运算
通过函数dot() 可实现数组元素的点积运算
clear all
A=[1 5 6 8 9 6]
B = [2 5 8 4 6 8]
c=dot(A,B)
d=sum(A.*B)
结果:
A =
1 5 6 8 9 6
B =
2 5 8 4 6 8
c =
209
d =
209
3.2.1 创建矩阵
1、希尔伯特矩阵 H阵
Hij = 1/(i+j-1)
由于他是一个条件数差的矩阵,所以将它用来作为实验矩阵
hilb(n) :用于生成一个n x n的希尔伯特矩阵
invhilb(n) :用于生成一个nxn的希尔伯特矩阵的逆矩阵整数矩阵
2、拓普利兹矩阵
3、0~1 之间均匀分布的随机矩阵
r=rand(n) 产生维数为n的0~1间均匀分布的随机矩阵
r=rand(m,n) 产生维数为nxm的0~1间均匀分布的随机矩阵
4、标准正态分布随机矩阵
r=randn()
格式可参考rand函数
5、魔方矩阵
魔方矩阵中的每行、每列和两条对角线上的元素和相等
M=magic(n)
6、帕斯卡矩阵
A = pascal(n)
7、范德蒙矩阵
A = vander(v)
clear all
A = vander([1 2 3 4])
B = vander([1; 2 ;3 ;4])
结果:
A =
1 1 1 1
8 4 2 1
27 9 3 1
64 16 4 1
B =
1 1 1 1
8 4 2 1
27 9 3 1
64 16 4 1
3.2.2 改变矩阵大小
表达式 **C=[A B] 在水平方向合并矩阵A和B
表达式C = [A ; B]**在竖直方向合并
矩阵行列的删除
要删除矩阵的某一行或一列,只需要把该行或列赋值为 ‘[]’ 即可
3.2.3 重构矩阵
矩阵的转置 ‘ 单引号
3.3.2 矩阵的乘法运算
矩阵与矩阵相乘
A*B
前行等后列
结果是前列后行
3.3.3 矩阵除法运算
矩阵除法是乘法的逆运算
分为左除和右除,分别用“”和“/”表示
3.3.4 矩阵的幂运算
当矩阵A为方阵时,可进行矩阵的幂运算
用“^”来进行幂运算
3.3.5 矩阵元素的查找
ind=find(X) 该函数查找矩阵X中的非零元素,函数返回这些元素的单下标
[row,col] = find(X,…) 返回双下标i和j
clear all;
A=[1 3 0
5 6 7
8 9 0];
B = find(A)
C = find(A>=5)
D = A(A>=1)
结果:
B =
1
2
3
4
5
6
8
C =
2
3
5
6
8
D =
1
5
8
3
6
9
7
线性索引
线性索引允许使用单个下标创建指向数组的索引,例如A(k)。MATLAB® 将该数组视为单列向量,其中每一列附加到前一列的底部。因此,线性索引从上到下、从左到右对列中的元素编号。
例如,假设一个 3×3 矩阵。您可以用 A(5) 来引用 A(2,2) 元素,用 A(8) 来引用 A(2,3) 元素。线性索引根据数组大小而改变;A(5) 会为 3×3 矩阵和 4×4 矩阵返回不同位置上的元素。
sub2ind 和 ind2sub 函数对于在下标和线性索引之间进行转换非常有用。
3.3.6 矩阵元素的排序
sort() 函数用来矩阵排序
clear all;
A=[1 3 0
5 6 7
8 9 0];
B=sort(A); %矩阵元素中按照列进行升序排列
C=sort(A,2); %矩阵元素中按照行进行升序排列
D=sort(A,'descend')%矩阵元素中按照列进行降序排列
E=sort(A,2,'descend')%矩阵元素中按照行进行降序排列
3.3.7 矩阵元素的求和
sum()函数
cumsum()函数
clear all;
A=[1 3 0
5 6 7
8 9 0];
B=sum(A) %矩阵元素中按照列进行求和
C=sum(A,2) %矩阵元素中按照行进行求和
D=cumsum(A) %矩阵中各列的和
E=cumsum(A,2)%矩阵中各行的和
结果:
B =
14 18 7
C =
4
18
17
D =
1 3 0
6 9 7
14 18 7
E =
1 4 4
5 11 18
8 17 17
3.3.8 矩阵元素的求积
prod() 函数
cumprod() 函数
用法同求和
3.3.9 矩阵元素的差分
顾名思义,就是在 矩阵 中,一行(一列)的元素与上一行(上一列)对应元素的差值,依次排列在上一行(上一列)元素对应所在位置。 矩阵元素的差分分为行差分和列差分,第一行和第一列不做差分计算。 上述的定义是定义 一阶差分 计算,若进行多阶矩阵元素的差分计算,仅需要进行迭代计算即可。
diff() 函数
clear all;
A=magic(3);
B=diff(A) %矩阵各列元素的差分
C=diff(A,2) %矩阵各列元素的2阶差分
D=diff(A,1,1) %矩阵各列元素的差分
E=diff(A,1,2) %矩阵各行列元素的差分
结果
B =
-5 4 1
1 4 -5
C =
6 0 -6
D =
-5 4 1
1 4 -5
E =
-7 5
2 2
5 -7
3.4.1 矩阵分析
这里线代没学好,还回去听了一遍,还没懂=_=,范数是个啥…
| 函数分析 | 功能描述 |
|---|---|
| norm | 求矩阵或者向量的范数 |
| normest | 估计矩阵的2阶范数 |
| rank | 矩阵的秩,即对角元素的和 |
| det | 矩阵的行列式 |
| trace | 矩阵的迹 |
| null | 0空间 |
| … | … |
1、向量和矩阵的范数运算
对于线性空间中的一个向量 x={x1,x2,…,xn},如果存在一个函数r(x)满足以下3个条件:
(1):r(x)>0,且r(x) = 0,的充分条件为0
(2): r(ax) = |a|r(x) , 其中a为标量
(3):对于向量x和y,有r(x+)<=r(x)+r(y)
则称r(x)为向量x的范数,一般记为||x||,范数的形式多种多样,eg:

稀疏矩阵
pass矩阵,真鸡儿难
第四章 MATLAB编程基础
4.2.2 变量类型
局部变量
全局变量
global X
永久变量
永久变量用persistent声明,只能在M文件函数中定义和使用,只允许他的函数存取。当声明他的函数退出时,MATLAB不会从内存中清除它
类似于C语言的static关键字
persistent X
4.2.3 MATLB默认的特殊变量
这些变量有时候会很有用,所以就把它们全写下来
| 特殊变量 | 描述 |
|---|---|
| ans | 系统默认的用作保存运算结果的变量名 |
| pi | 圆周率 |
| eps | 机器零阈值,MATLAB中最小数 |
| inf | 表示无穷大 |
| NaN或nan | 表示不定数 |
| i或j | 虚数 |
| nargin | 函数的输入参数个数 |
| nargout | 函数的输出参数个数 |
| realmain | 可用的最小正实数 |
| realmax | 可用的最大正实数 |
| bitmain | 可用最大正整数(以双精度格式存储 |
| varargin | 可变的函数输入参数个数 |
| vararout | 可变的函数输出个数 |
| beep | 使计算机发出“嘟嘟”的声音 |
4.2.4 关键字
'break'
'case'
'catch'
'classdef'
'continue'
'else'
'elseif'
'end'
'for'
'function'
'global'
'if'
'otherwise'
'parfor'
'persistent'
'return'
'spmd'
'switch'
'try'
'while'
4.3.1顺序结构
4.3.2 if-else-end 分支结构
4.3.3 switch-case 结构
switch value
case test1
command1
case test2
command2
....
otherwise
end
4.3.4 try-catch结构
try
command1 %命令组1总是首先被执行。若正确,执行完后结束此结构
catch
command2 %命令组1执行发生错误时执行命令组2
end
4.3.4 for循环结构
for x=array
commands
end
4.3.4 while循环结构
while expression
commands
end
4.4.1 return指令
4.4.2 input和output指令
Value = input('请输入数字')
Value = input('巴拉巴拉','s')
第一种调用方式,用户可以输入数值、字符串等各种形式的数据
第二中调用方式,用户无论输入什么内容,均以字符串形式赋值
当遇到keyboard指令时,MATLAB将控制权暂时交给键盘,用户可以由键盘输入各种可发的MATLAB指令,只有当用户输入完成,并输入ruturn执行后,空主权才还给matlab
intput和keyboard的不同之处在于:ketboard指令语序输入任意多个matlab指令,而input只允许用户属兔赋值给变量的值,即数组、字符串、或元胞数组等。
4.4.3 yesinput指令
yesinput指令是一个只能输入的指令,它提供一个默认值,并对输入范围进行检查
这个函数好像有点问题,在matlab2016a上运行时说没有这个函数,用的不多,暂时就不细究了…
4.4.4 pause指令
pause指令的功能为控制执行文件的暂停与恢复
pause %暂停执行文件,等待用户按任意键继续
pause(n) %在继续执行文件之前,暂停n秒
4.4.5 continue指令
4.4.6 break指令
error和warning指令
error(‘message’) :显示出错信息,终止程序
waring(‘message’):显示警告信息,继续运行程序
4.5.2 函数
若M文件的第一个可执行语句以function开始,改文件就是函数文件,每一个函数文件都定义一个函数
4.5.3M文件的一般结构
函数参数指令集
| 数据格式 | 说明 |
|---|---|
| nargin | 指定调用函数所带参数的个数 |
| nargout | 指定调用函数所返回的参数的个数 |
| inputname(x) | 返回输入表上数值x所在位置的输入参数变量的名字。如果用一个表达式代替已命名的参数,则返回一个空字符串 |
4.5.4 匿名函数、子函数、私有函数与私有目录
匿名函数创建方法
f = @(input1,input2,..) expression
f为创建的函数句柄,函数句柄是一种间接访问函数的途径,可以使用户调用函数的过程中变得很简单,减少程序设计的繁杂
子函数
在matlab中,多个函数的diamante可以同时写到一个M函数文件中。其中,出现的第一个函数称为主函数,该文件中的其他函数称为子函数,保存时所用的函数文件名应当与主函数定义名相同,外部程序只能对主函数进行调用
子函数书写规范:
1): 每个子函数的第一行是其函数声明行
2): 在M函数文件中,主函数的位置不能改变,但是多个子函数的排列顺序可以任意改变
3): 子函数只能被处于同一M文件中的主函数或其他子函数调用
4): 在M函数文件中,任何指令通过名称对函数进行调用时,子函数间的信息传递可通过输入/输出变量、全局变量或跨空间指令来实现
私有函数与私有目录
1、私有函数的构造与普通M函数完全相同
2、关于私有函数的调用:私有函数只能被private直接父目录下的M文件所调用,而不能被其他目录下 的任何M文件或matlab指令窗口的命令所调用
3、在M文件中,任何指令通过“名称”对函数进行调用时,私有函数的优先级仅次于matlab内置函数和子函数
4.5.5重载函数
4.5.6 eval和feval函数
eval(s):该指令的功能为使用matlab的注释器求表达式的值或执行包含文本字符串s的语句
feval函数的具体句法形式:
[y1,y2,...] = feval('FN',arg1,arg2,...)
该指令的功能为用变量arg1,arg2,…来执行FN函数指定的计算
4.5.7 内联函数
不推荐使用 inline。请改用 匿名函数。
在以后版本会取消inline,在此不做介绍
4.5.8 向量化和预分配
1、向量化
想让matlab最高效工作,重要的是在M文件中把算法向量化。其他程序语言可能用for多DO循环,matlab则可用向量或矩阵运算
2、预分配
若一条代码不能向量化,则可以通过预分配任何输出结果已保存其中的向量或数组以加快for循环
4.5.9 函数的函数
一种以标量为变量的非线性函数称为“函数的函数”,即以函数名为自变量的函数。这类函数包括求零点、最优化、求积分和常微分方程。
4.5.10 P码文件
一个M文件首次被调用时,matlab将首先对该M文件进行语法分析,并把生成的相应内部伪代码文件存放在内存中。
当M文件在此被调用时,将直接调用该M文件在内存中的P码文件,而不会再对原M文件进行重复的语法分析
第五章 数据可视化
5.1.1离散数据及离散函数
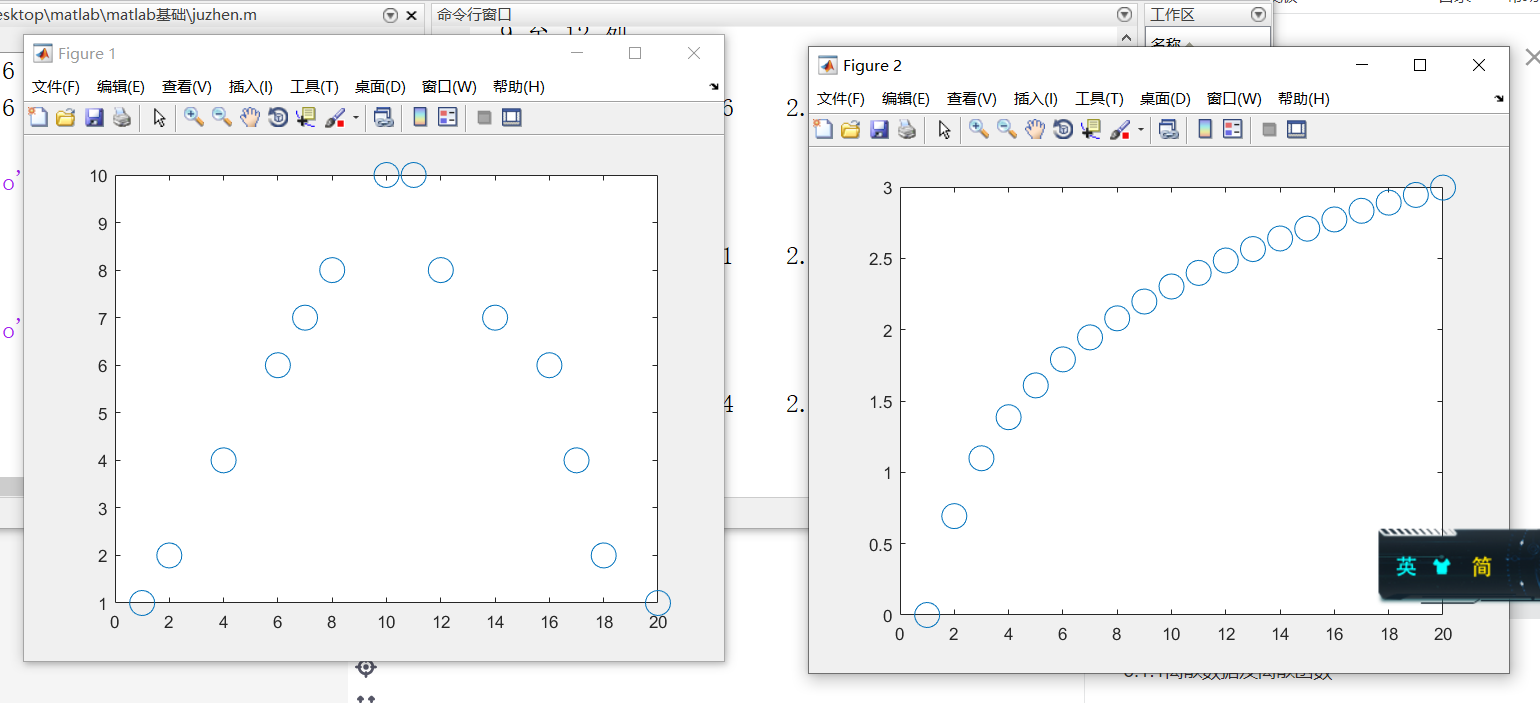
x1 = [1 2 4 6 7 8 10 11 12 14 16 17 18 20]
y1 = [1 2 4 6 7 8 10 10 8 7 6 4 2 1]
figure(1)
plot(x1,y1,'o','MarkerSize',15)
x2 = 1:20
y2 = log(x2)
figure(2)
plot(x2,y2,'o','MarkerSize',15)
5.1.2 连续函数
在matlab中是无法画出真正的连续的函数的,因此在实现连续函数的可视化时,首先必须将连续函数用一组离散自变量上计算函数结果,然后将自变量数组和结果数组在图形中表示出来。
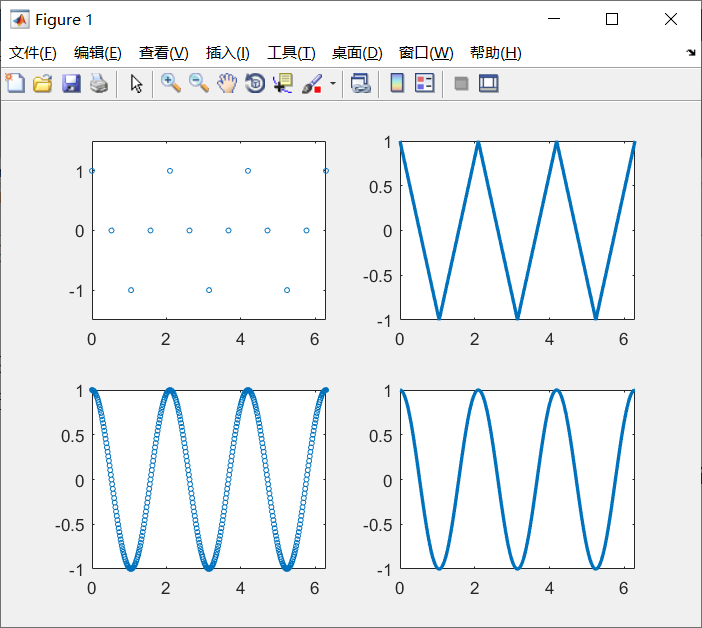
x1 = (0:12)*pi/6;y1 = cos(3*x1);
x2 = (0:360)*pi/180; y2 = cos(3*x2);
figure(1)
subplot(2,2,1);plot(x1,y1,'o','MarkerSize',3);xlim([0 2*pi]);ylim([-1.5 1.5])
subplot(2,2,2);plot(x1,y1,'LineWidth',2);xlim([0 2*pi])
subplot(2,2,3);plot(x2,y2,'o','MarkerSize',3);xlim([0 2*pi])
subplot(2,2,4);plot(x2,y2,'LineWidth',2);xlim([0 2*pi])
5.1.3 图形绘制示例
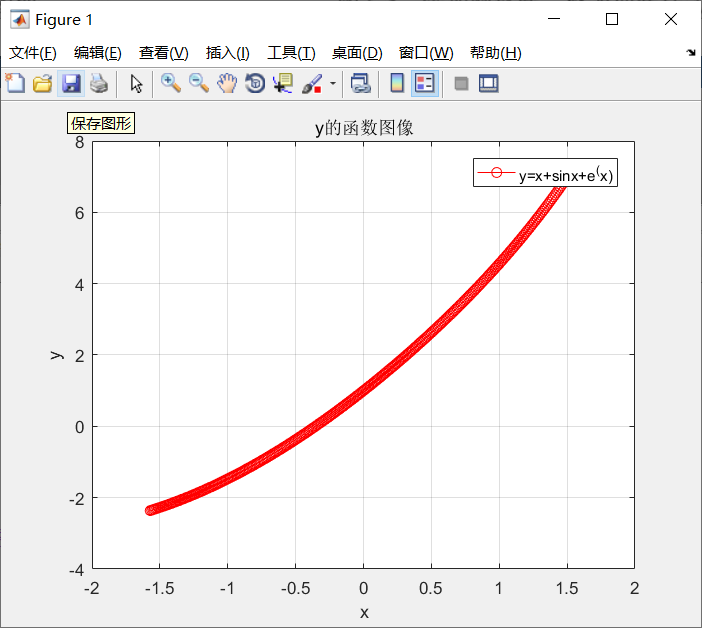
画出 y=x+sinx+ex,画出在x在(- π 2 frac{π}{2} 2π, π 2 frac{π}{2} 2π)上的图像。。。什么编辑器
x = -pi/2:0.01:pi/2;
y = x+sin(x)+exp(x);
plot(x,y)
plot(x,y,'-ro')
grid on
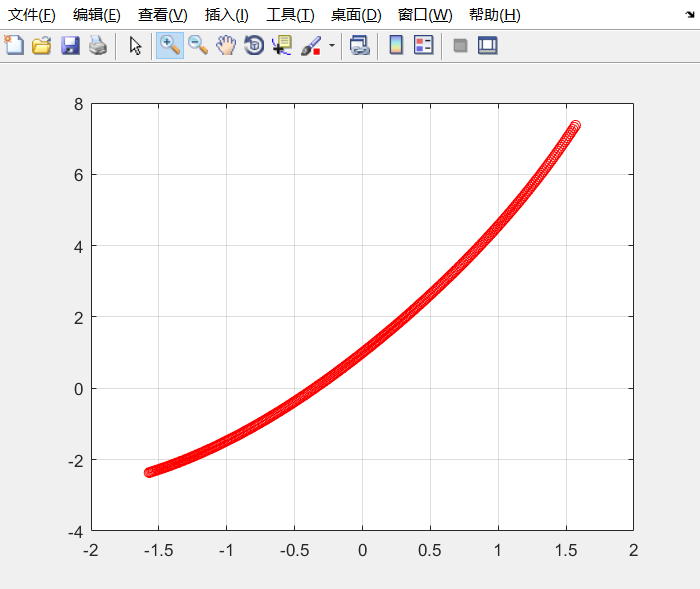
plot(x,y,’-ro’)
-ro 就是红色的圈,放大红色粗线会发现红色的圈
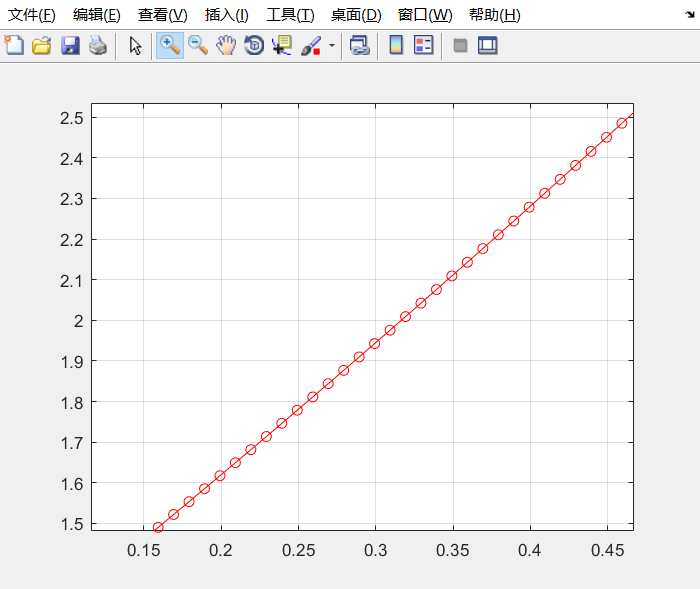
给图像添加注释
title('y的函数图像');
xlabel('x');
ylabel('y');
legend('y=x+sinx+e^(x)')
5.2.1 plot指令
一般使用规范
1)plot(x,y)
2)plot(y)
其中y为一维实数数组,以1:n为横坐标,yi为纵坐标,绘制曲线(n为y的长度)
3)plot(z)
其中z为一维复数数组,以横轴为实轴,纵轴为虚轴,在复平面上绘制(real(zj),imag(zj))的有序集合的图形
4)plot(A)
绘制矩阵A的列对它下标的图形。对于mxn的矩阵A,有n和含有m个元素的数对,或是有n条有m个点的曲线,且这n条曲线均采用颜色监视器上不同的颜色绘制而成
… … . … … . … … …
5.2.2 栅格
grid on命令可以在当前图形的单位标记处添加栅格
grid off 可以取消栅格
5.2.3 文字说明
| 指令 | 说明 |
|---|---|
| title(‘text’) | 在图形窗口顶端的中间位置输出字符串text’作为标题 |
| xlabel(‘text’) | 在x轴下的中间位置输出字符串’text’作为标注 |
| ylabel(‘text’) | 在y轴上的中间位置输出字符串’text’作为标注 |
| zlabel(‘text’) | 在z轴上的中间位置输出字符串’text’作为标注 |
| text(x,y,‘text’) | 在图形窗口的(x,y)处写字符串‘text’ |
| legend(str1,str2,…,‘Location’,‘pos’) | pos可选:North、South、East、…分别代表图形的不同位置 |
legendoff 从当前图形中清除图例
在matlab中 sqrt(-1) 求-1的算术平方根
结果会是一个复数 0.0000 + 1.0000i
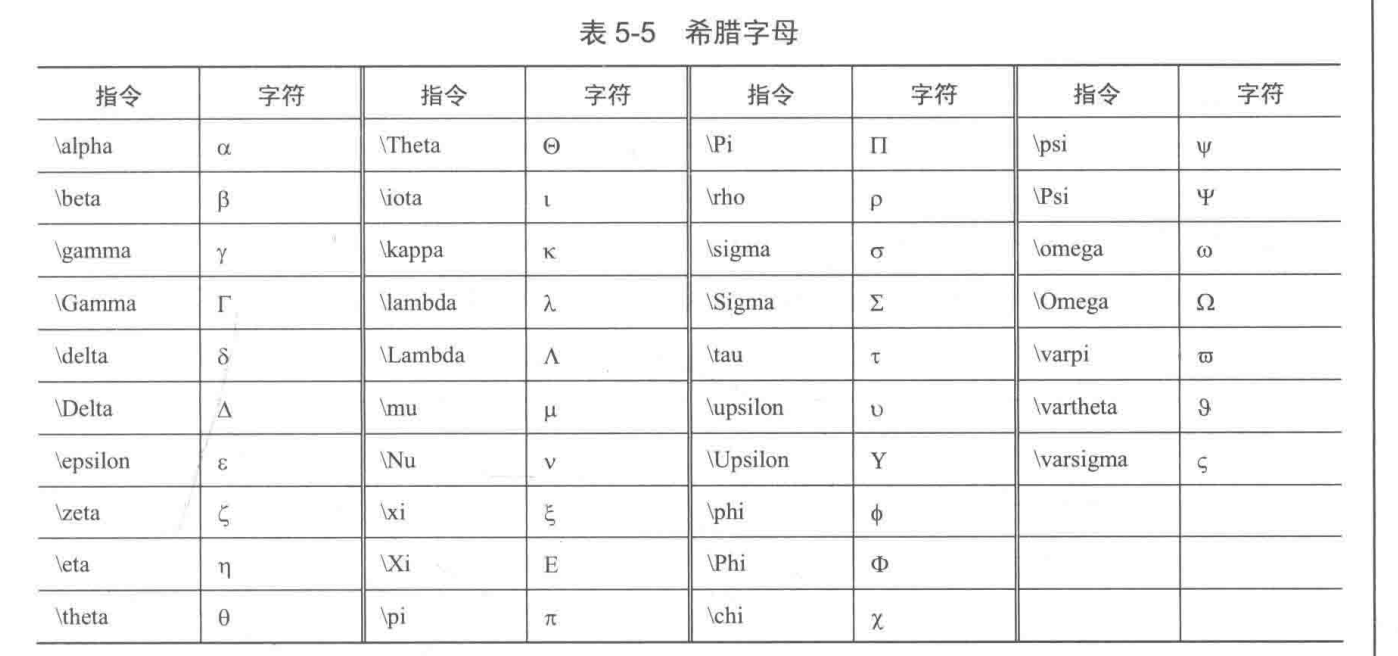
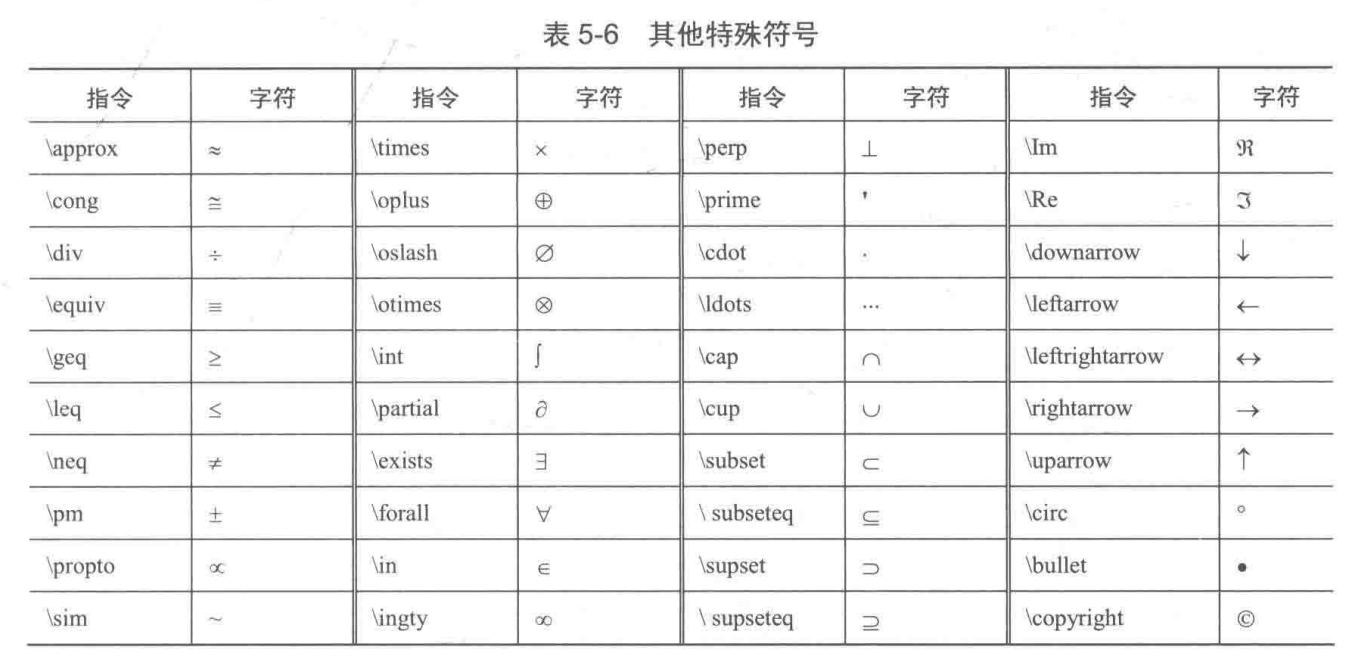
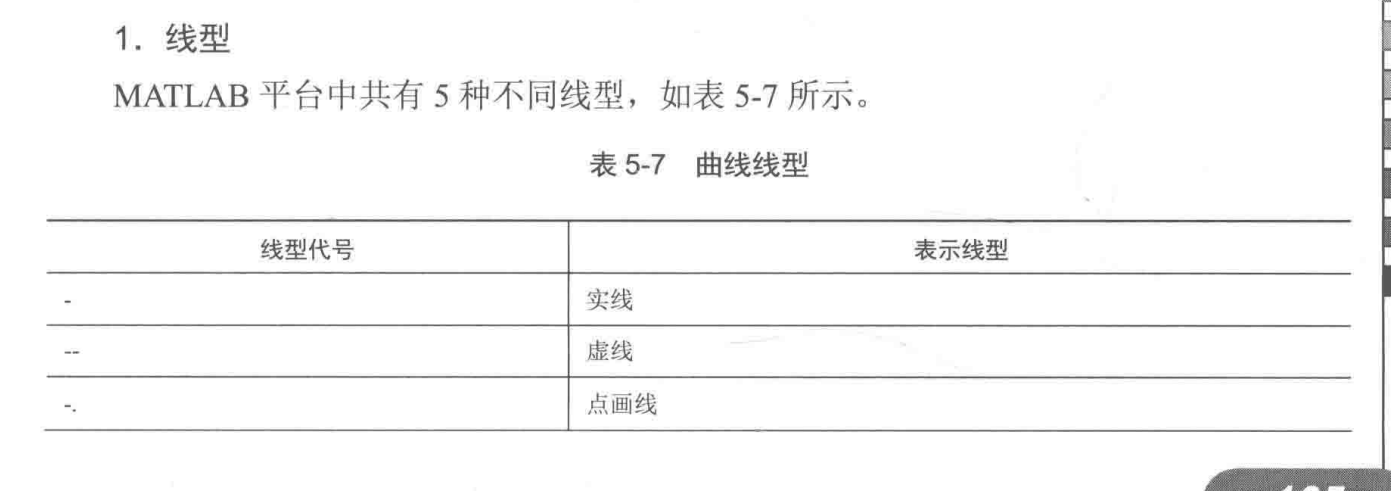
5.2.4 线型、标记和颜色
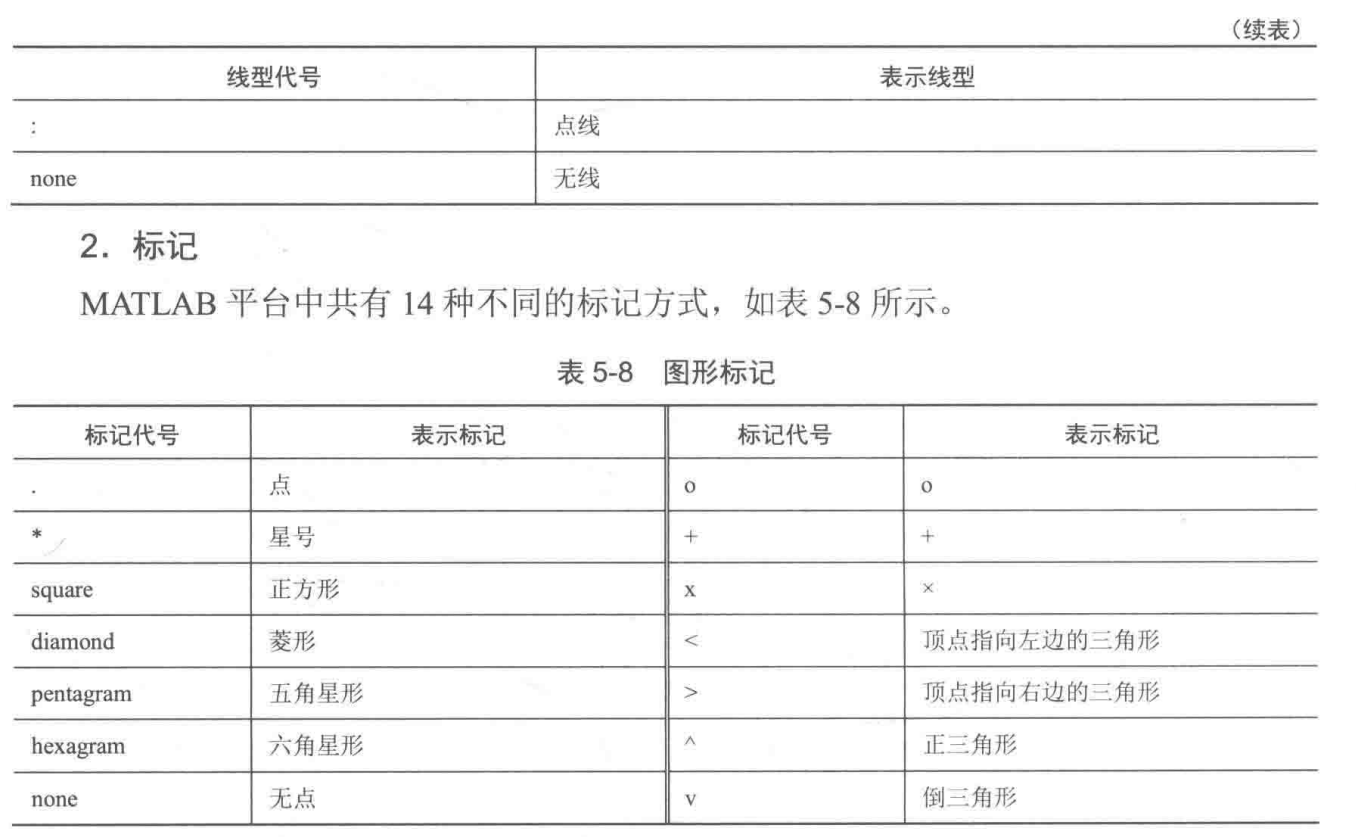
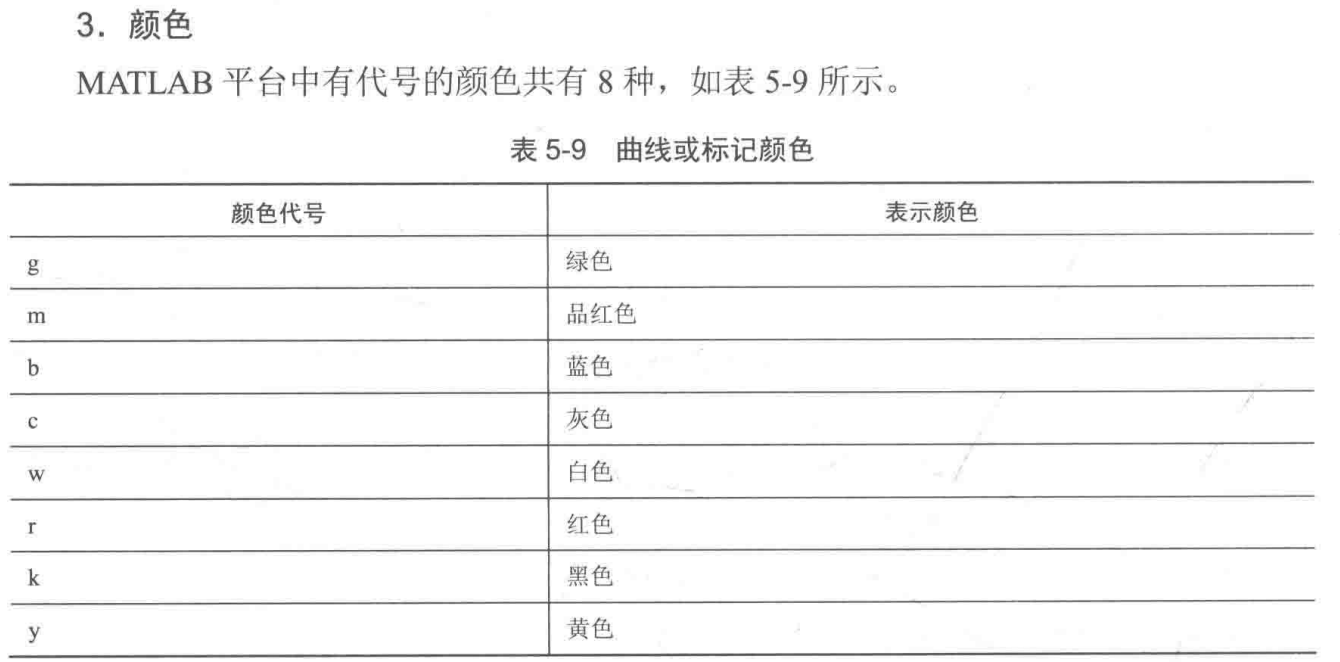
5.2.6 图形叠绘
hold on :语句功能为使当前轴及图形保留下来而不被刷新,并接收即将绘制的新的曲线
hold off :语句功能为不保留当前轴及图形,并接收即将绘制的新的曲线
5.2.7 子图绘制 subplot
matlab允许用户在同一个图形窗口中同时绘制多副相互独立的子图,用到subplot指令
subplot(m,n,k): 将(mxn)幅子图中的第k幅作为当前曲线的绘制图
subplot(‘position’,[left bottom width height]): 在指定位置上生成子图,并作为当前曲线的绘制图
绘图这里挖个坑,后面有实际练手的东西再回来补
x1=[81 153 181 227 244 250 251 210 181 179 201 217 212 190 166 179 181 174 145 87 34 ];
y1=[226 192 184 160 125 112 97 68 71 85 86 98 121 135 133 85 71 63 70 171 181 ];
x2=[145 161 174 ];
y2=[70 81 63 ];
x3=[201 208 ];
y3=[86 81 ];
x4=[217 224 ];
y4=[98 94 ];
x5=[244 295 314 279 233 221 181 ];
y5=[125 79 80 127 172 177 184 ];
x6=[279 311 331 282 233 ];
y6=[127 116 121 153 172 ];
x7=[282 298 281 244 221 ];
y7=[153 160 167 177 177 ];
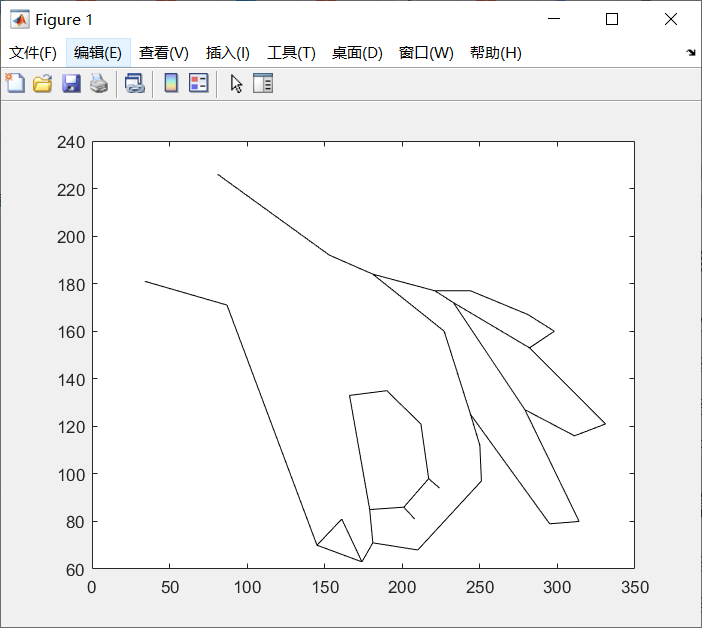
plot(x1,y1,'k',x2,y2,'k',x3,y3,'k',x4,y4,'k',x5,y5,'k',x6,y6,'k',x7,y7,'k')
一堆线哈哈
在这里插入图片描述
第六章 数据分析
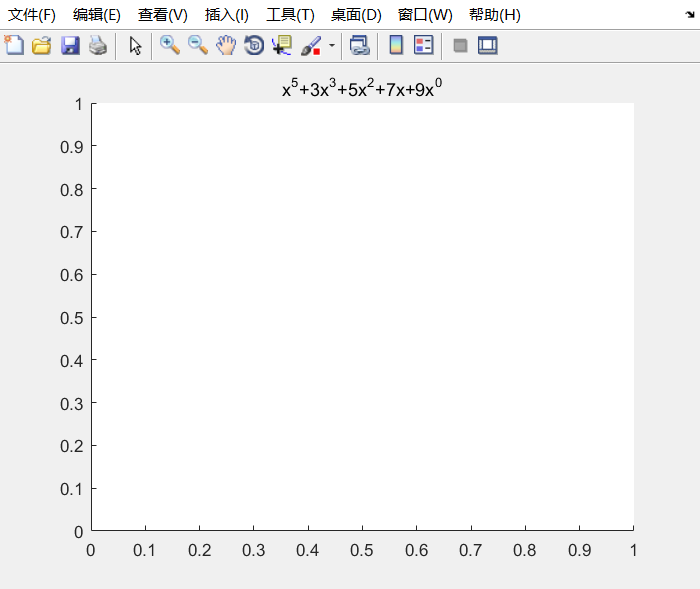
6.1.1 多项式的表达式的创建
通过系数矩阵表达多项式
strcat 即 Strings Catenate,横向连接字符串。
语法
combinedStr= strcat(s1, s2, …, sN)
function s = part6(p)
%这个1个l太像了,傻傻分不清
if nargin>1
error('Too much input arguments')
end
while p(1)==0
p(1)=[] ; %将高次0去掉
end
l = length(p);
if(l==0)
s = '0';
elseif l==1
s = num2str(p(1))
elseif l==2
s=strcat(num2str(p(1)),'x+',num2str(p(2)));
elseif l>2
for i = 1:l
if i==1
if p(i)==1
s=strcat('x^{',num2str(l-i),'}');
else
s=strcat(num2str(p(i)),'x^{',num2str(l-i),'}');
end
elseif i==1
s=strcat(s,'+',num2str(p(i))');
elseif i==l-1
s=strcat(s,'+',num2str(p(i)),'x');
else
if p(i)==0
else
s=strcat(s,'+',num2str(p(i)),'x^{',num2str(l-i),'}');
end
end
end
end
6.1.2 多项式求根
提供特定函数
roots() 求解方程式的根

由根创建多项式
poly()
6.1.3 多项式的四则运算
多项式乘法
在MATLAB中,函数conv支持多项式乘法(运算法则为执行两个数组的卷积)
多项式除法
deconv函数
6.1.4 多项式的导数、积分与估值
1、多项式导数
polyder函数

2、多项式的积分
polyint函数
polyint(P,k) 返回多项式P的积分,积分常数项为k
polyint§ 返回多项式P的积分,积分常数项默认为0
3、多项式的估值
polyval函数
6.1.5 多项式运算函数及操作指令
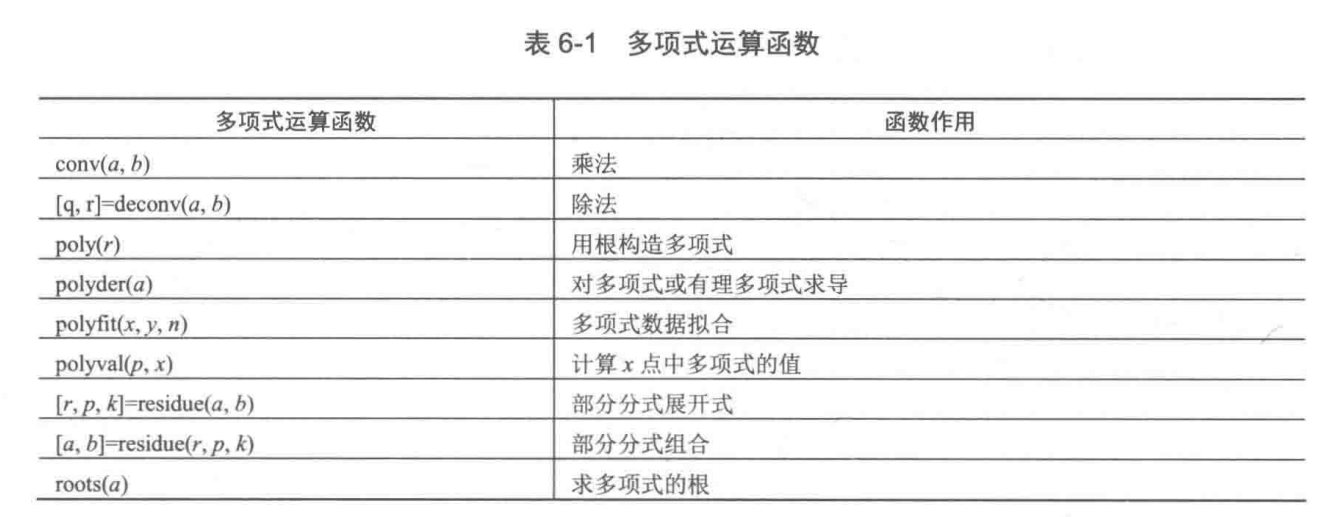
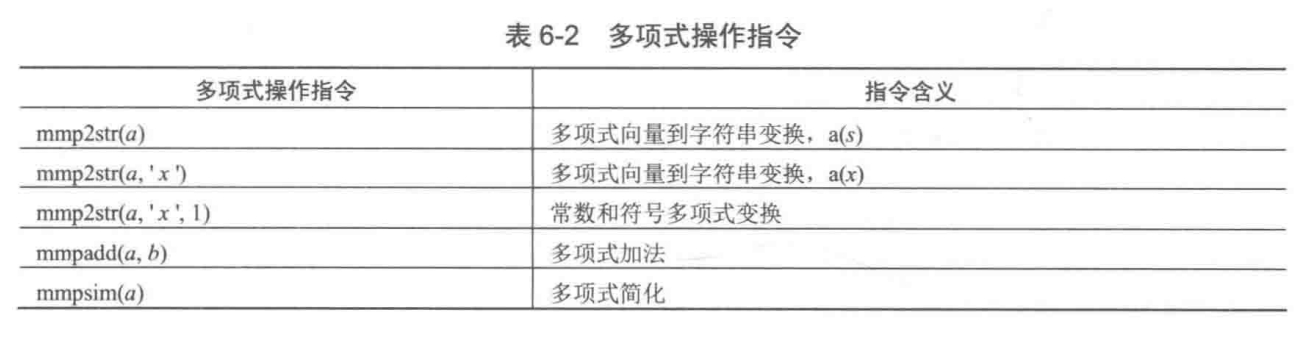
6.1.6 有理多项式
有理多项式由他们的分子多项式和分母多项式表示。对有理多项式进行运算的两个函数是 residue 和 polyder。含糊 residue执行部分分式展开的运算
6.2.1 数据插值 一维插值
最后
以上就是安静画板最近收集整理的关于啃 matlab一本通读书笔记摘要第一章 2016a概述第二章 matlab基础知识第三章 数组与矩阵第四章 MATLAB编程基础第五章 数据可视化第六章 数据分析的全部内容,更多相关啃内容请搜索靠谱客的其他文章。








发表评论 取消回复