1. 首页
  2. 文章中心
  3. matlab

数字通信——MSK调制解调，维特比解码下误码率与信噪比之间的关系前言一、MSK是什么？二、仿真代码图像

86 阅读 0 评论
我是靠谱客的博主 俊秀金毛，最近开发中收集的这篇文章主要介绍数字通信——MSK调制解调，维特比解码下误码率与信噪比之间的关系前言一、MSK是什么？二、仿真代码图像，觉得挺不错的，现在分享给大家，希望可以做个参考。

概述

前言

一个实现数字通信下msk调制与解调的MATLAB仿真，以及利用维特比算法实现维特比解码。通过维特比解码来实现最大似然解码的一些个人见解，最后得出信噪比与误码率之间的图像。

一、MSK是什么？

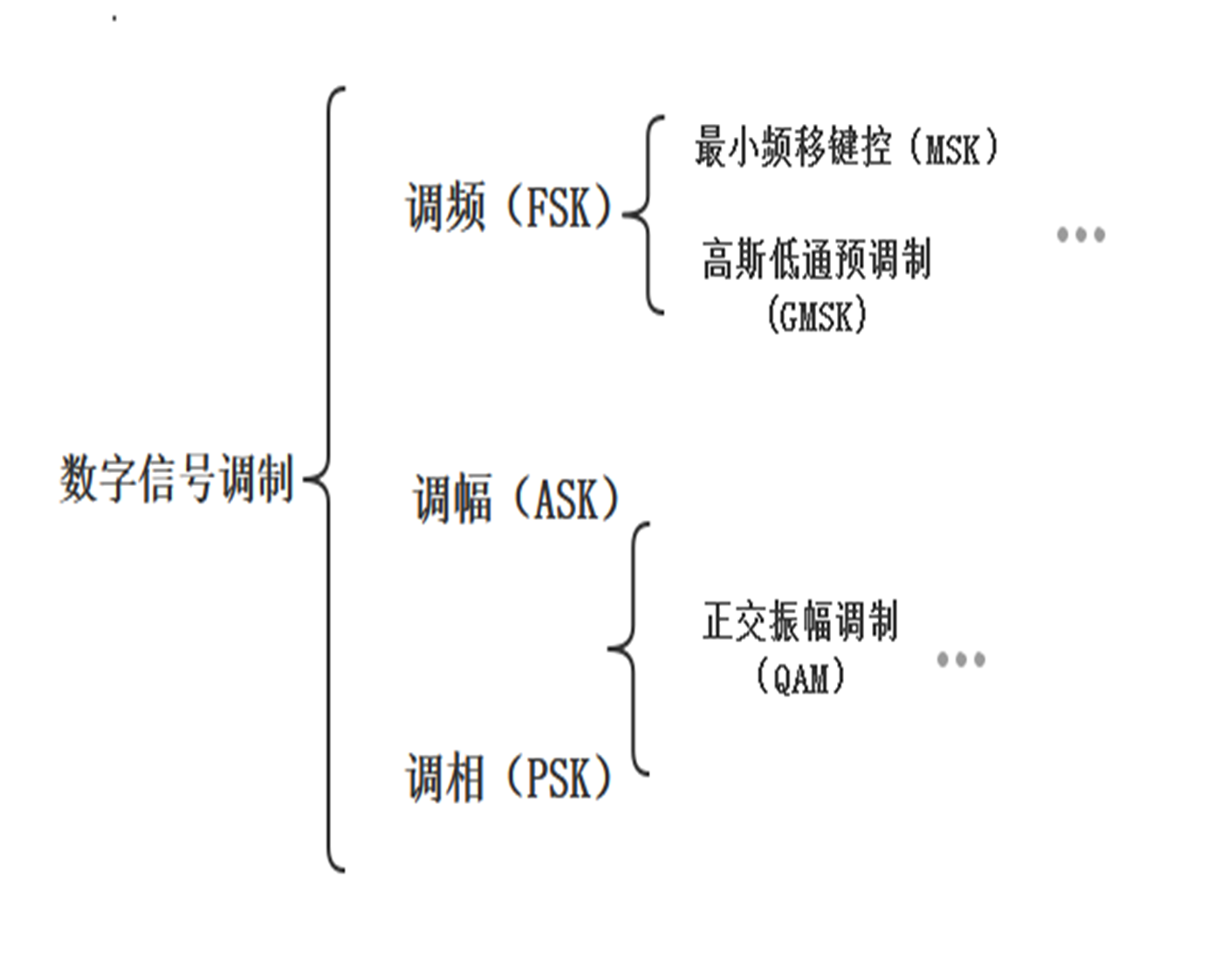
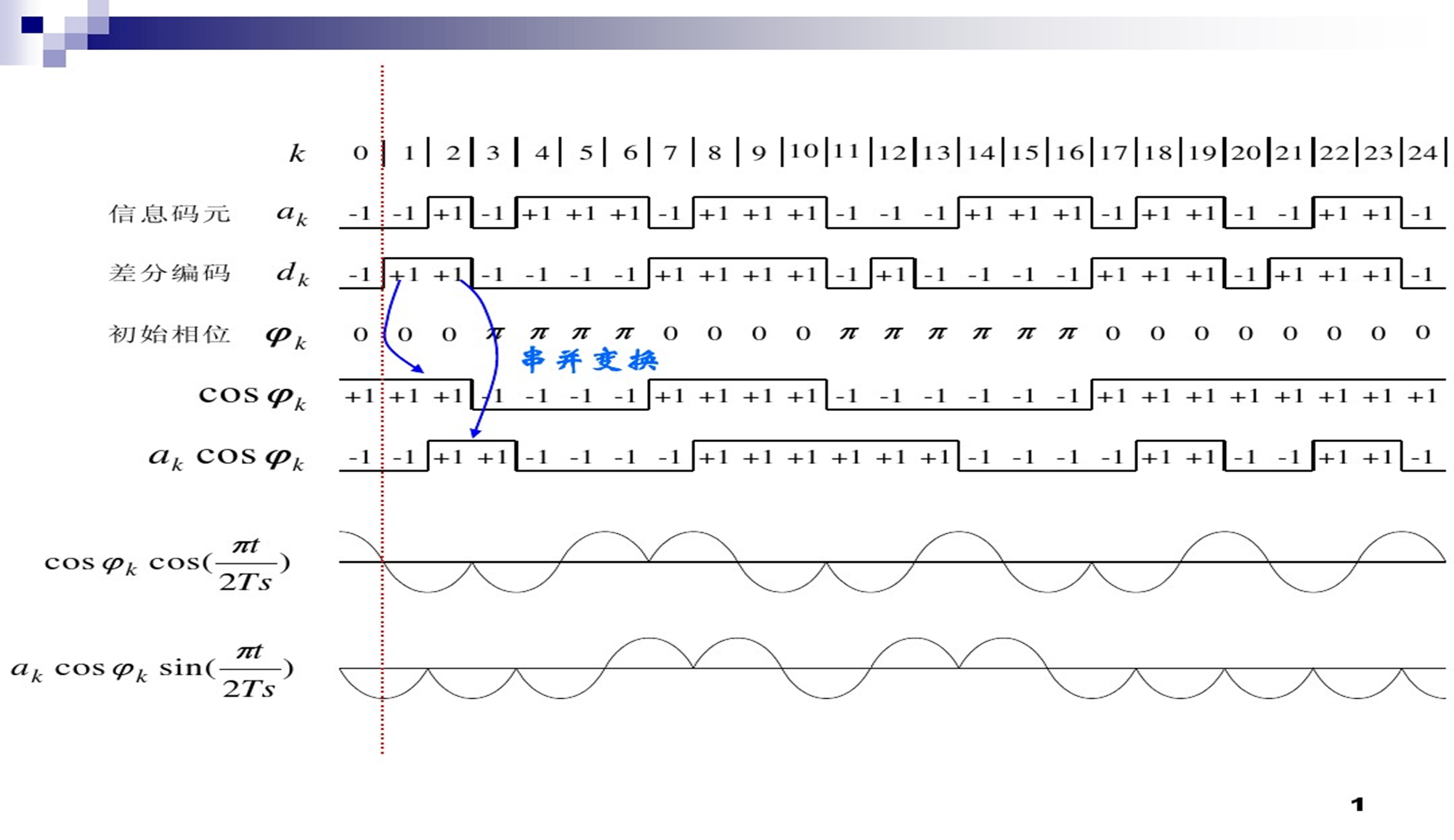
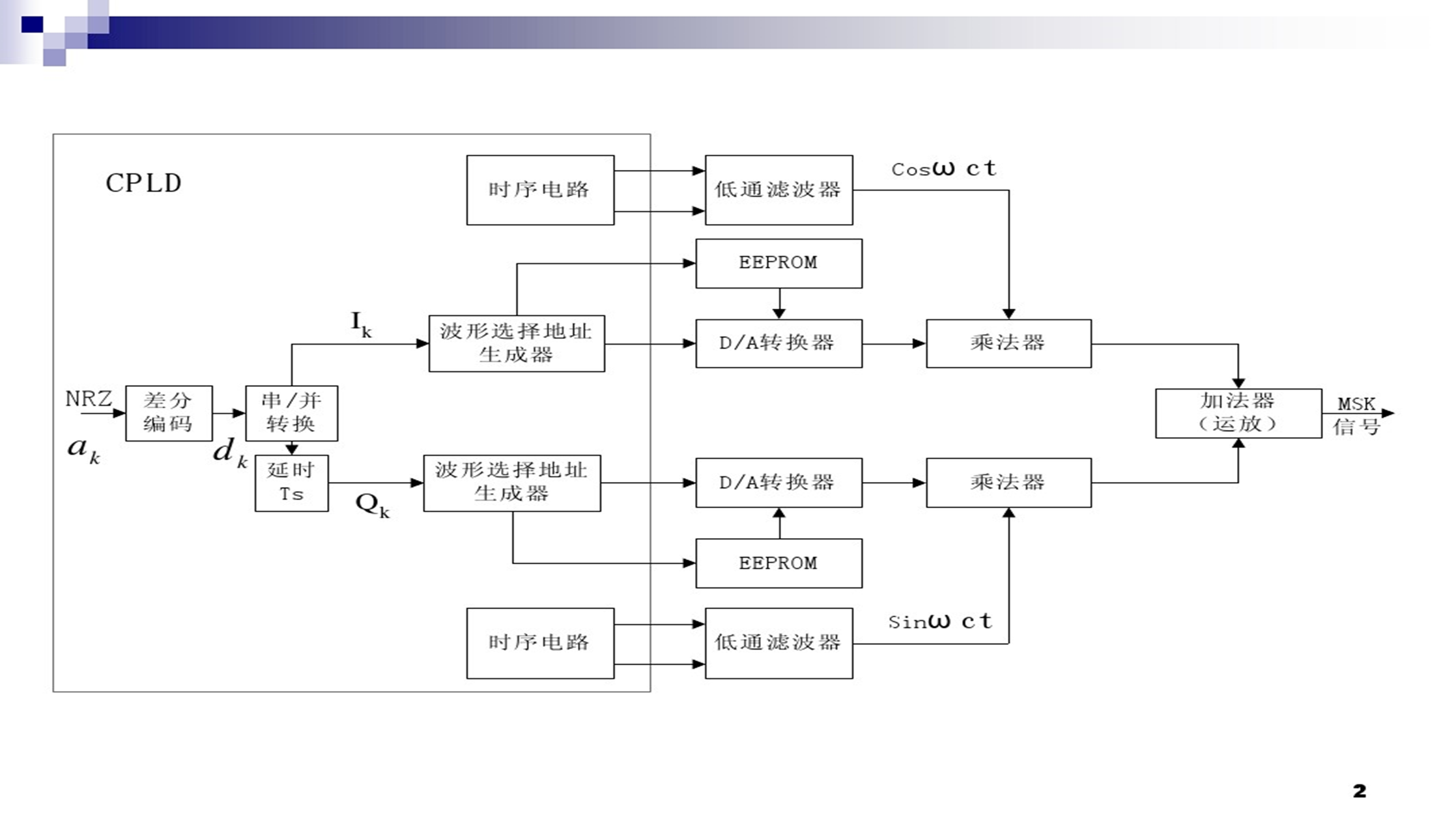
在这里插入图片描述在这里插入图片描述
在这里插入图片描述

在这里插入图片描述
在这里插入图片描述

在这里插入图片描述

在这里插入图片描述
在这里插入图片描述

在这里插入图片描述

二、仿真代码

clear all
close all
clc

%-------------------------------------------------------------------------%
%                                PART 1.1                                 %
%-------------------------------------------------------------------------%

N = 1e4; % 10^5
A = 1;
T = 0.01;

% 生成一个符号序列{-1,1}
b = (sign(randn(1,2*N))+1)/2;
for i=1:1:length(b) 
    if b(i)==0
        b(i)=-1;
    end
end

% 应用递归方程对QPSK中的符号进行变换
% symbols
xQ_1 = -1;
x_1 = 1;
xI_n = zeros(1,N);
xQ_n = zeros(1,N);
for n=1:1:N
    if n==1
        xI_n(n) = -xQ_1*x_1;
        xQ_n(n) = -xI_n(n)*b(n);
    elseif n~=1 
        xI_n(n) = -xQ_n(n-1)*b(2*(n-1));
        xQ_n(n) = -xI_n(n)*b(2*n-1);
    end
end

xI_n; %  同相分量
xQ_n; %  正交分量
z_n = xI_n + 1i*xQ_n; % Add in - phase and quadrature component to create z_n

% 计算误码率
iter = 1e2; 
SNR_dB = 5;
SNR_lin = 10.^(SNR_dB/10); % 10log_10(SNR_lin)
BER_appr = 0;

for p=1:1:iter
    n = randn(1,N) + 1i*randn(1,N);
    y_n = A*T*z_n + sqrt(A^2*T^2/SNR_lin)*n;
    y_Re = sign(real(y_n)); % 当出现负数时返回-1，否则返回1
    y_Im = sign(imag(y_n));
    BER_appr = BER_appr + sum(y_Im ~= imag(z_n)) + sum(y_Re ~= real(z_n));
end
BER = BER_appr/(N*iter);

D = ['BER = ', num2str(BER)];
disp('------------------------------------------------------------------------------------------------------------------------------------');
disp('An approximation for BER - Bit Error Rate with SNR = 5 dB is:');
disp(D);
disp('------------------------------------------------------------------------------------------------------------------------------------');

SNR_dB_B = 5:12; % Values of SNR in dB
SNR_lin_B = 10.^([5:12]/10); % Values of SNR in decimal

BER_B = zeros(1,length(SNR_lin_B));
BER_appr_B = zeros(1,length(SNR_lin_B));

for k=1:1:length(SNR_lin_B)
    for p=1:1:iter
        n = randn(1,N) + 1i*randn(1,N);
        y_n = A*T*z_n + sqrt(A^2*T^2/SNR_lin_B(k))*n;
        y_Re = sign(real(y_n)); % returns -1 when a negative number occur and 1 otherwise
        y_Im = sign(imag(y_n));
        BER_appr_B(k) = BER_appr_B(k) + sum(y_Im ~= imag(z_n)) + sum(y_Re ~= real(z_n));
    end
    BER_B(k) = BER_appr_B(k)/(2*N*iter);
    Theory_BER(k) = 0.5*erfc(sqrt(SNR_lin_B(k))); % theoretical BER
end

disp(['SNR in dB : ' num2str(SNR_dB_B)]);
disp(['BER Measured : ' num2str(BER_B)]);
disp(['BER Theoretical : ' num2str(Theory_BER)]);
disp('------------------------------------------------------------------------------------------------------------------------------------');

figure(1)
semilogy(SNR_dB_B,BER_B,'b-*') 
xlabel('SNR (dB)')
ylabel('BER - Bit Error Rate Measured')
title('BER - Bit Error Rate vs SNR_{dB}')
grid on

figure(2)
semilogy(SNR_dB_B,BER_B,'b-*') 
hold on
semilogy(SNR_dB_B,Theory_BER,'m-o')
xlabel('SNR (dB)')
ylabel('BER - Bit Error Rate Measured & Theoretical')
title('BER - Bit Error Rate vs SNR_{dB}')
legend('BER - Measured', 'BER - Theoretical')
grid on

%-------------------------------------------------------------------------%
%                                PART 1.2                                 %
%-------------------------------------------------------------------------%

SNR_dB_C = 5;
SNR_lin_C = 10.^(SNR_dB_C/10);

% Creating the symbols x(n) in set {-1,1}
b = (sign(randn(1,N))+1)/2;
for i=1:1:length(b) 
    if b(i)==0
        b(i)=-1;
    end
end

% Constructing the vectors s_1 & s1
% s_1 is for s^(-1)
% s1 is for s^1
s_1 = [-(2*A*sqrt(T)*1i)/pi; (A*sqrt(T)*sqrt(pi^2 - 4))/pi];
s1  = [A*sqrt(T); 0];

beta = (A^2*T)/SNR_lin_C; % From equation (16)
var = 2*beta;
BER_Viterbi = 0; %initialising BER

for p=1:1:iter
    n1_n = sqrt(var)*(randn(1,N) + 1j*randn(1,N)); % Generating the values of the noise vector n1_n
    n2_n = sqrt(var)*(randn(1,N) + 1j*randn(1,N));
    phase(1) = 0;
    for n=1:1:N
        phase(n+1) = phase(n) + b(n)*pi/2;
        if b(n) == -1 
            r_n(:,n) = s_1.*exp(1i*phase(n)) + [n1_n(n); n2_n(n)]; % if x(n) == -1
        elseif b(n) == 1
            r_n(:,n) = s1.*exp(1i*phase(n)) + [n1_n(n); n2_n(n)];  % if x(n) == 1
        end
    end
    x_opt = Viterbi(N,s1,s_1,r_n);
    BER_Viterbi = BER_Viterbi + sum(b~=x_opt); 
end
BER_Viterbi = BER_Viterbi/(2*N*iter);

disp('An approximation for BER - Bit Error Rate with Viterbi aglgorithm and SNR = 5 dB is:');
disp(['BER = ', num2str(BER_Viterbi)])
% disp(['BER Theoretical : ' num2str(Theory_BER)]);
disp('------------------------------------------------------------------------------------------------------------------------------------');

% Creating the BER diagram for SNR = 5,6,7,8,9,10,11,12
SNR_dB_E = 5:12;
SNR_lin_E = 10.^(SNR_dB_E/10);
BER_Viterbi_E = zeros(1,length(SNR_lin_E));
BER_Viterbi_appr_E = zeros(1,length(SNR_lin_E));

% Constructing the vectors s_1 & s1
s_1 = [-(2*A*sqrt(T)*1i)/pi; (A*sqrt(T)*sqrt(pi^2 - 4))/pi];
s1  = [A*sqrt(T); 0];

for k=1:1:length(SNR_lin_E)
    for p=1:1:iter
        n1_n = sqrt(A^2*T/SNR_lin_E(k))*(randn(1,N) + 1j*randn(1,N)); % Generating the values of the noise vector n1_n
        n2_n = sqrt(A^2*T/SNR_lin_E(k))*(randn(1,N) + 1j*randn(1,N));
        phase(1) = 0;
        for n=1:1:N
            phase(n+1) = phase(n) + b(n)*pi/2;
            if b(n) == -1 
                r_n(:,n) = s_1.*exp(1i*phase(n)) + [n1_n(n); n2_n(n)]; % if x(n) == -1
            elseif b(n) == 1
                r_n(:,n) = s1.*exp(1i*phase(n)) + [n1_n(n); n2_n(n)];  % if x(n) == 1
            end
        end
        x_opt = Viterbi(N,s1,s_1,r_n);
        BER_Viterbi_appr_E(k) = BER_Viterbi_appr_E(k) + sum(b~=x_opt);
        Theory_BER_Viterbi(k) = 0.5*erfc(sqrt(SNR_lin_E(k))); % theoretical BER
    end
    BER_Viterbi_E(k) = BER_Viterbi_appr_E(k)/(2*N*iter);
end

disp(['SNR in dB : ' num2str(SNR_dB_E)]);
disp(['BER Measured : ' num2str(BER_Viterbi_E)]);
disp(['BER Theoretical : ' num2str(Theory_BER_Viterbi)]);
disp('------------------------------------------------------------------------------------------------------------------------------------');


figure(3)
semilogy(SNR_dB_E,BER_Viterbi_E,'b-*') 
xlabel('SNR (dB)')
ylabel('BER - Bit Error Rate Measured ')
title('BER - Bit Error Rate vs SNR_{dB} - Viterbi Algorithm')
grid on

figure(4)
semilogy(SNR_dB_E,BER_Viterbi_E,'b-*'),
hold on
semilogy(SNR_dB_B,BER_B,'g-*'),
hold on
semilogy(SNR_dB_B,Theory_BER,'m-o')
xlabel('SNR (dB)')
ylabel('BER - Bit Error Rate Measured & Theoretical')
title('BER - Bit Error Rate vs SNR_{dB}')
legend('BER - Viterbi','BER - Measured', 'BER - Theoretical','Location','southwest')
grid on

2.维特比算法代码

function [x_opt] = Viterbi(N, s1, s_1, r_n)

%-------------------------------------------------------------------------%
%                                 FORWARD                                 %
%-------------------------------------------------------------------------%

pointer_pi(1) = -1;     
pointer_0(1) = -1;

for n=1:1:N
    if n==1
        w_3pi2(n) = real(r_n(:,n)'*s_1*exp(1i*0)); % 第一步
        w_pi2(n) = real(r_n(:,n)'*s1*exp(1i*0));   
    elseif n~=1
        if mod(n,2)==0 % Even bits
            % Even symbols can end up ONLY with phase pi or 0
            
            % From 3pi/2 to pi with symbol -1
            % From 3pi/2 to 0 with symbol +1
            w3pi2_pi(n) = real(r_n(:,n)'*s_1*exp(1i*3*pi/2));
            w3pi2_0(n) = real(r_n(:,n)'*s1*exp(1i*3*pi/2));
            
            % From pi/2 to pi with symbol +1
            % From pi/2 to 0 with symbol -1
            wpi2_pi(n) = real(r_n(:,n)'*s1*exp(1i*pi/2));
            wpi2_0(n) = real(r_n(:,n)'*s_1*exp(1i*pi/2));

            % The cost may be the weight(3pi/2, pi) + the weight of the
            % last symbol 3pi/2 due to the memory property of the phase.
            % The cost may be the weight(pi/2, pi) + the weight of the
            % last symbol pi/2 due to the memory property of the phase.
            total_cost_1 = w3pi2_pi(n) + w_3pi2(n-1);
            total_cost_2 = wpi2_pi(n) + w_pi2(n-1);
            [w_pi(n),pointer_pi(n)] = max([total_cost_1 0 total_cost_2 0]);
            
            % The cost may be the weight(3pi/2, 0) + the weight of the
            % last symbol 0 due to the memory property of the phase.
            % The cost may be the weight(pi/2, 0) + the weight of the
            % last symbol 0 due to the memory property of the phase.
            total_cost_1 = w3pi2_0(n) + w_3pi2(n-1);
            total_cost_2 = wpi2_0(n) + w_pi2(n-1);
            [w_0(n),pointer_0(n)] = max([total_cost_1 0 total_cost_2 0]);
            
        elseif mod(n,2)~=0 % Odd bits
            % Odd symbols can end up ONLY with phase 3pi/2 or pi/2
            
            % From 0 to 3pi/2 with symbol -1
            % From 0 to pi/2 with symbol +1
            w0_3pi2(n) = real(r_n(:,n)'*s_1);
            w0_pi2(n) = real(r_n(:,n)'*s1);
            
            % From pi to 3pi/2 with symbol +1
            % From pi to pi/2 with symbol -1
            wpi_3pi2(n) = real(r_n(:,n)'*s1*exp(1j*pi));
            wpi_pi2(n) = real(r_n(:,n)'*s_1*exp(1j*pi));
            
            % The cost may be the weight(pi, 3pi/2) + the weight of the
            % last symbol pi due to the memory property of the phase.
            % The cost may be the weight(0, 3pi/2) + the weight of the
            % last symbol 0 due to the memory property of the phase.
            total_cost_1 = wpi_3pi2(n) + w_pi(n-1);
            total_cost_2 = w0_3pi2(n) + w_0(n-1);
            [w_3pi2(n),pointer_3pi2(n)] = max([0 total_cost_1 0 total_cost_2]);

            % The cost may be the weight(pi, pi/2) + the weight of the
            % last symbol pi due to the memory property of the phase.
            % The cost may be the weight(0, pi/2) + the weight of the
            % last symbol 0 due to the memory property of the phase.
            total_cost_1 = wpi_pi2(n) + w_pi(n-1);
            total_cost_2 = w0_pi2(n) + w_0(n-1);
            [w_pi2(n),pointer_pi2(n)] = max([0 total_cost_1 0 total_cost_2]);
        end
    end
end

%-------------------------------------------------------------------------%
%                                 BACKWARD                                %
%-------------------------------------------------------------------------%

% 只保留给出最大权重和的路径
if mod(n,2)~=0
    [~,route(N+1)] = max([w_3pi2(n) 0 w_pi2(n) 0]);
elseif mod(n,2)==0
    [~,route(N+1)] = max([0 w_pi(n) 0 w_0(n)]);
end

route(1) = 4;
for n=N:-1:1
    if n~=1
        if mod(n,2)==0 % Even symbols
            [~,p] = max([0 w_pi(n) 0 w_0(n)]);
            enter = [0 pointer_pi(n) 0 pointer_0(n)];
            route(n) = enter(p);
        elseif mod(n,2)~=0 % Odd symbols
            [~,p] = max([w_3pi2(n) 0 w_pi2(n) 0]);
            enter = [pointer_3pi2(n) 0 pointer_pi2(n) 0];
            route(n) = enter(p);
        end
    end
    route;
    
    % Restoring the symbols 
    if route(n)-route(n+1)==-1
        x_opt(n) = -1;
    elseif route(n)-route(n+1)==1
        x_opt(n) = 1;
    elseif route(n)-route(n+1)==-3
        x_opt(n) = 1;
    elseif route(n)-route(n+1)==3
        x_opt(n) = -1;
    end  
    
end

end

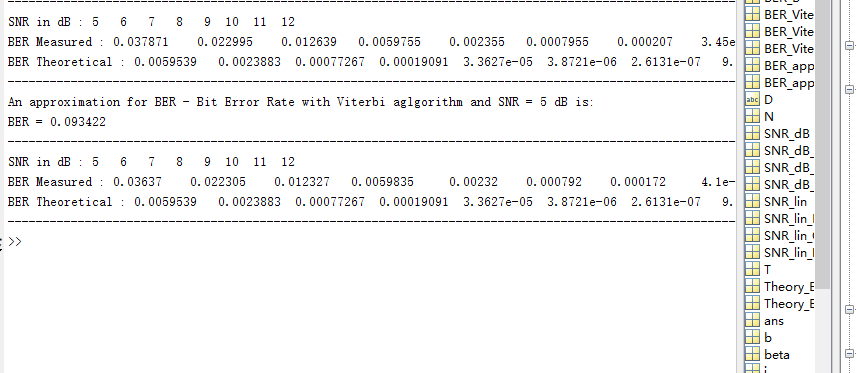
在这里插入图片描述

图像

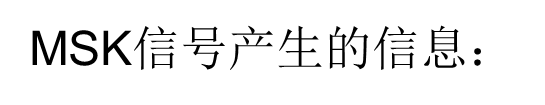
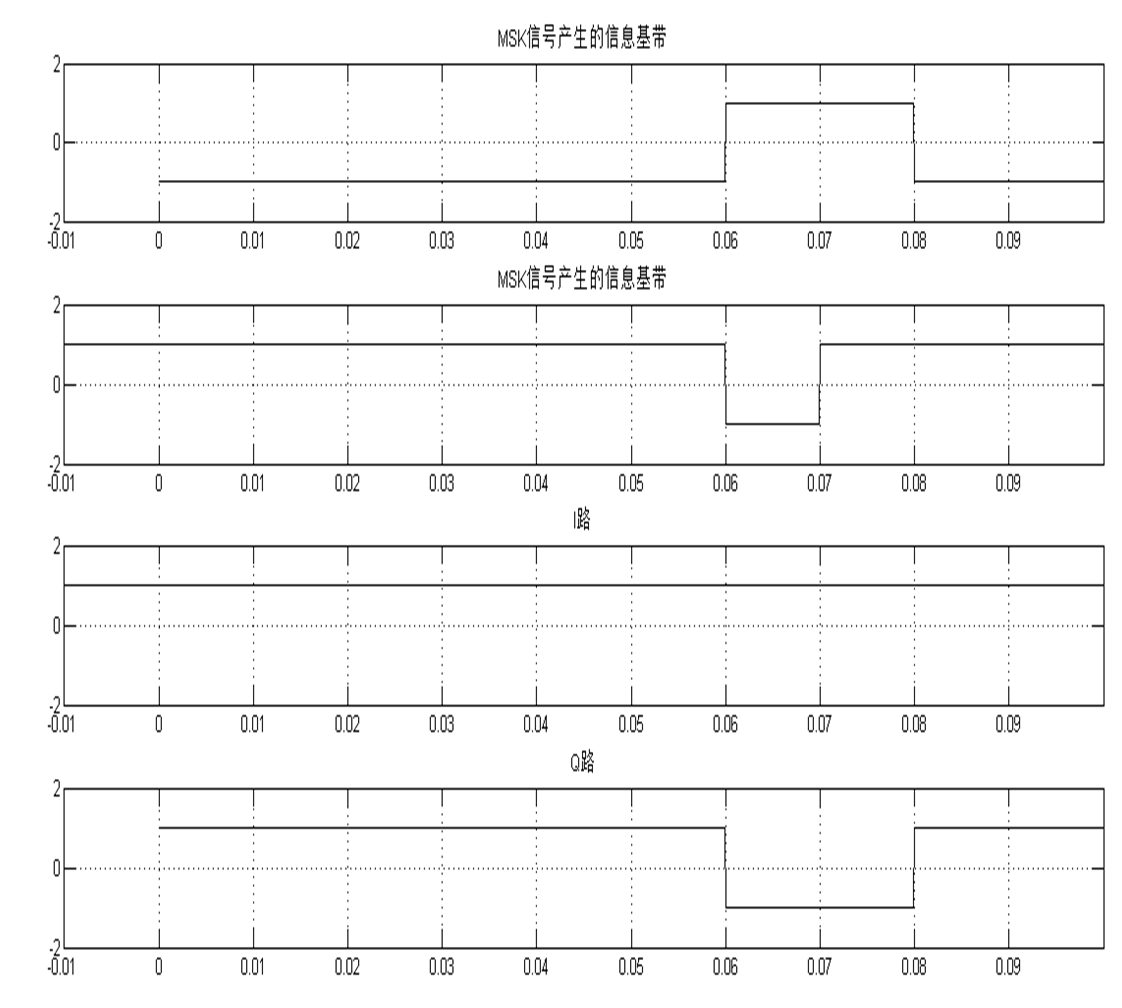
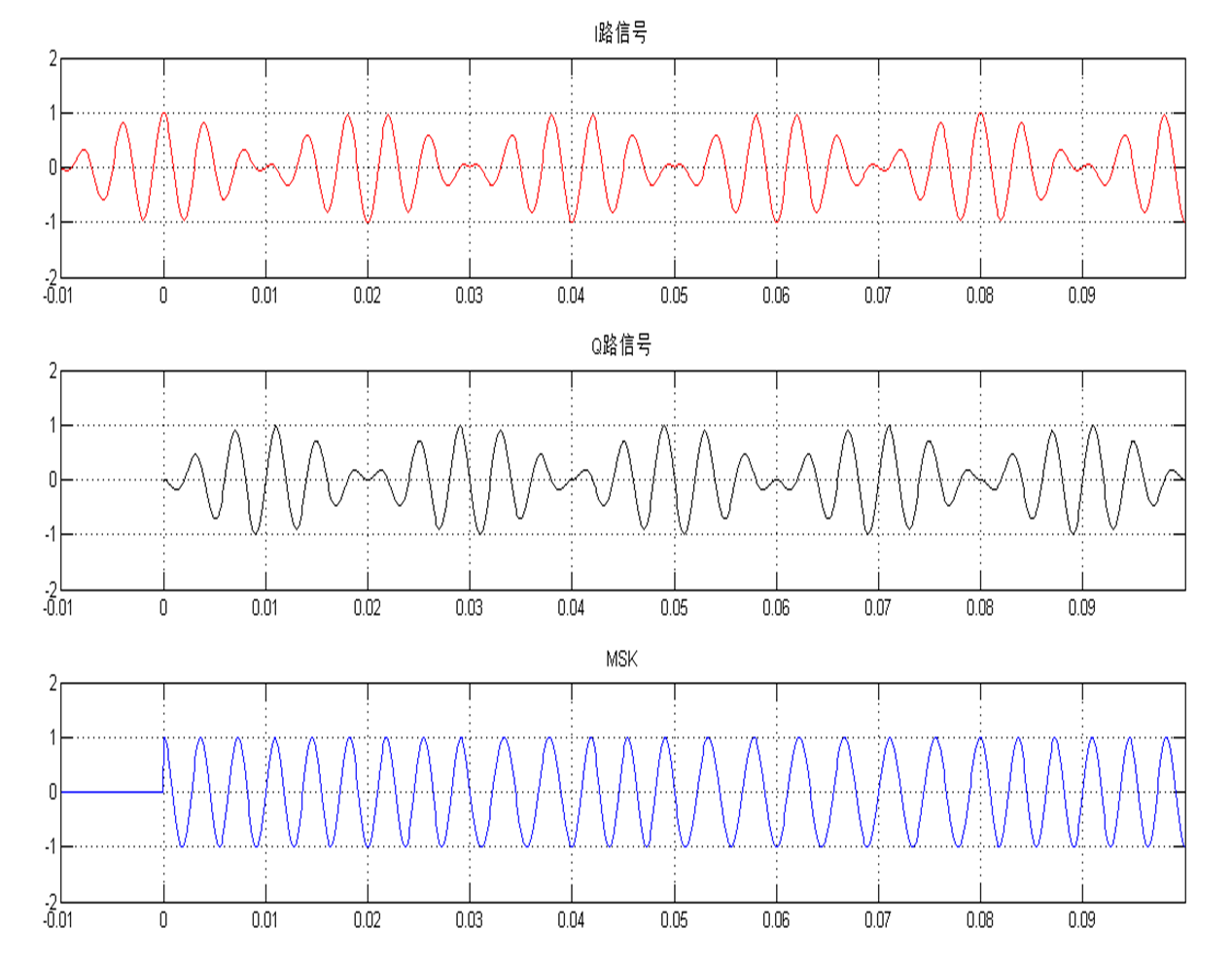
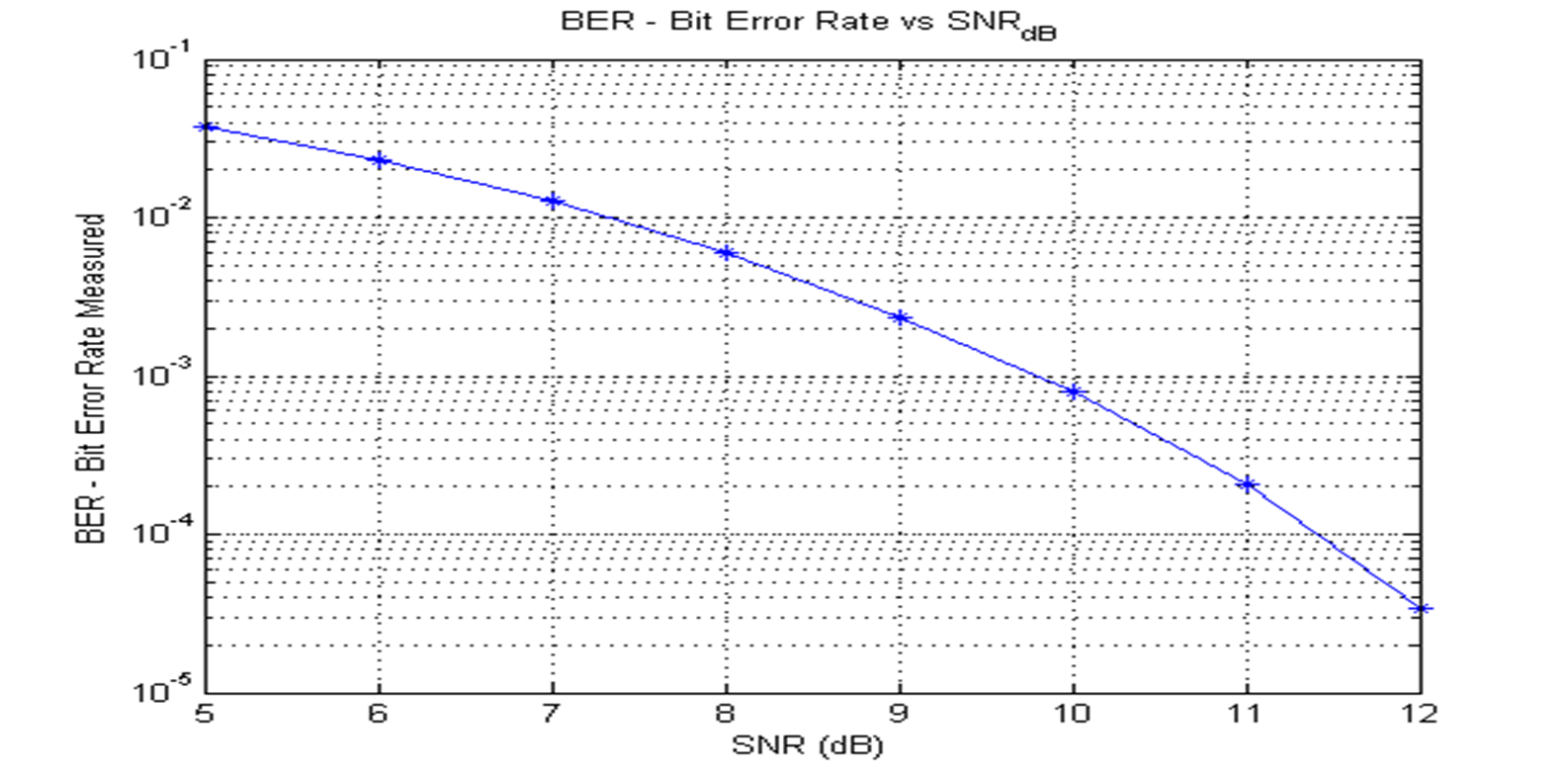
在这里插入图片描述

在这里插入图片描述在这里插入图片描述
在这里插入图片描述
信噪比与误码率的函数图像：

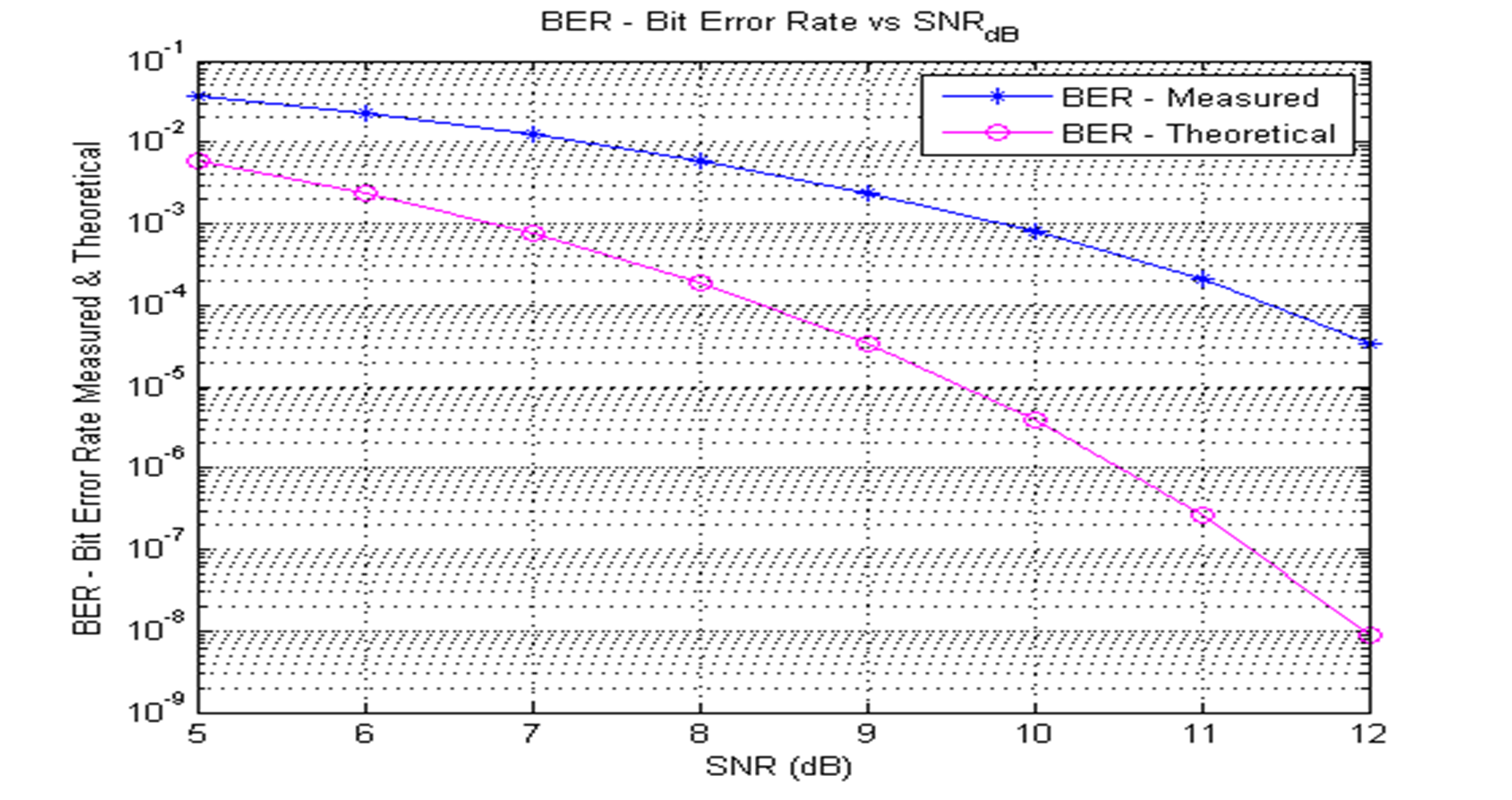
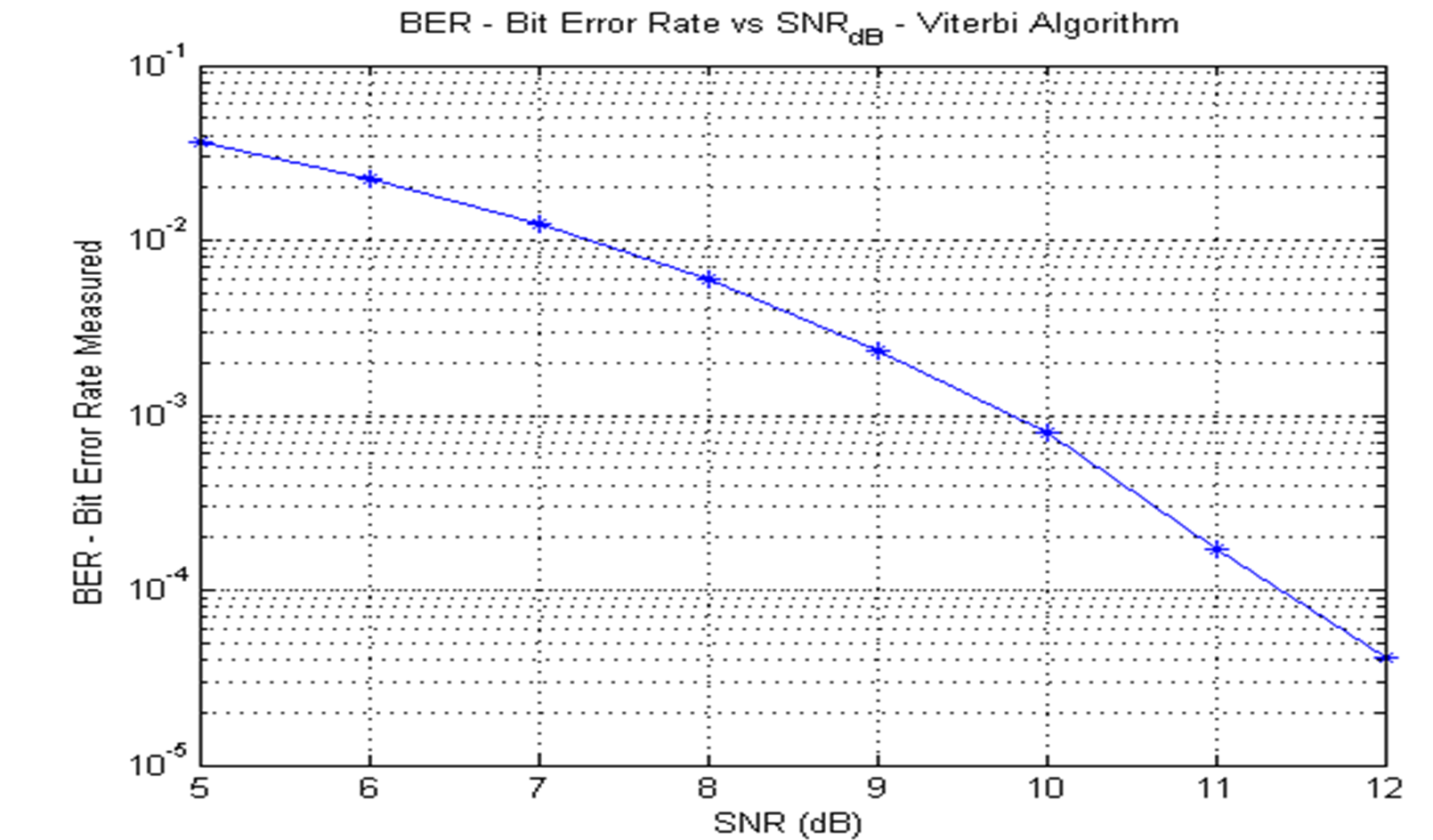
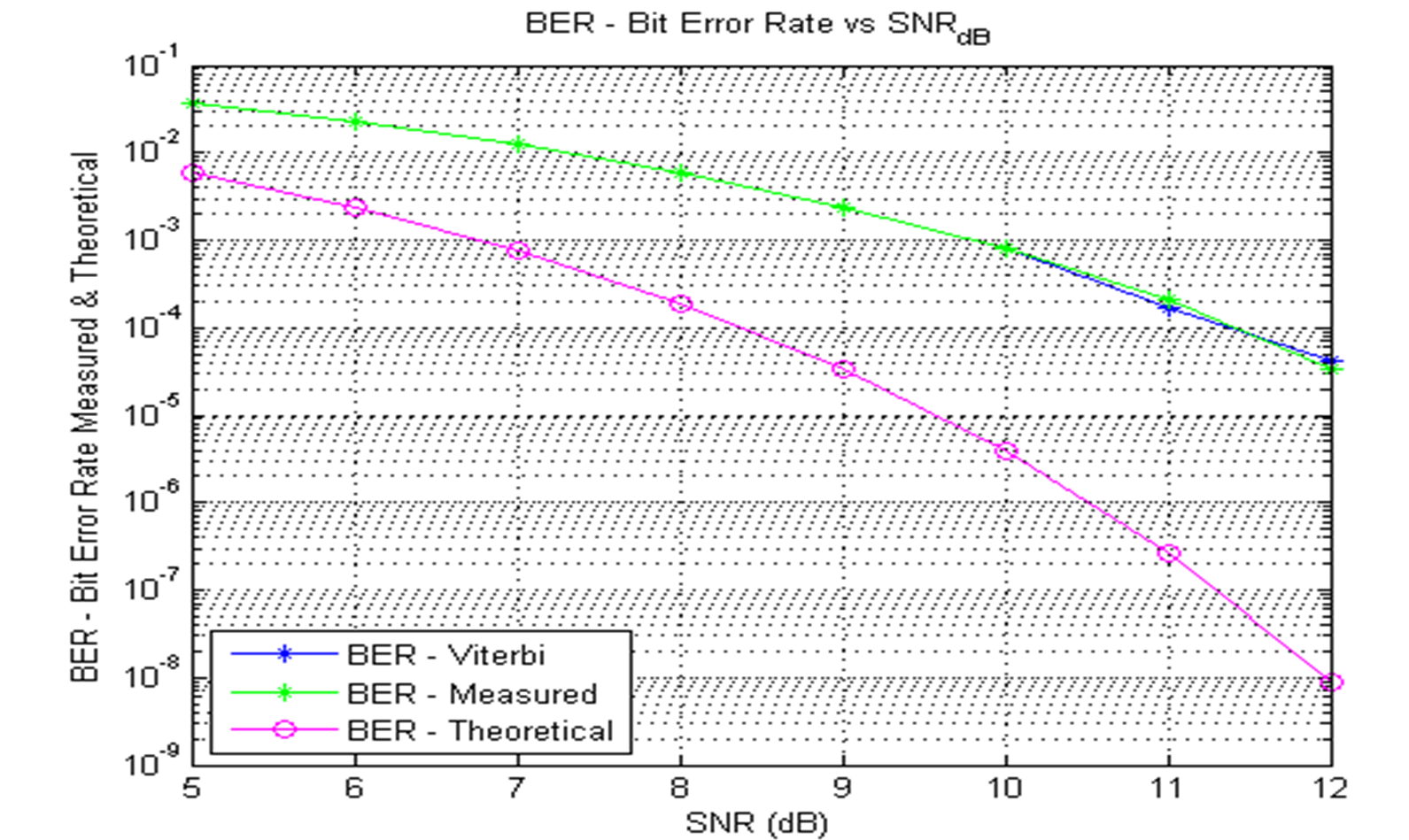
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述

在这里插入图片描述

最后

以上就是俊秀金毛为你收集整理的数字通信——MSK调制解调，维特比解码下误码率与信噪比之间的关系前言一、MSK是什么？二、仿真代码图像的全部内容，希望文章能够帮你解决数字通信——MSK调制解调，维特比解码下误码率与信噪比之间的关系前言一、MSK是什么？二、仿真代码图像所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。

本图文内容来源于网友提供，作为学习参考使用，或来自网络收集整理，版权属于原作者所有。
点赞(57)

相关文章

误码率与信噪比的关系matlab,一种误码率和信噪比关系的分析方法与流程
误码率与信噪比的关系matlab,一种误码率和信噪比关系的分析方法与流程
关于信噪比SNR【转载】
关于信噪比SNR【转载】
通信常识
通信常识
手机GPS 搜星 根据信燥比 判断 信号强弱
手机GPS 搜星 根据信燥比 判断 信号强弱
数字通信——MSK调制解调，维特比解码下误码率与信噪比之间的关系前言一、MSK是什么？二、仿真代码图像
数字通信——MSK调制解调，维特比解码下误码率与信噪比之间的关系前言一、MSK是什么？二、仿真代码图像
瑞丽噪声与信噪比的关系_一篇文章看懂散粒噪声
瑞丽噪声与信噪比的关系_一篇文章看懂散粒噪声
Python办公自动化教程-1.3节: 项目实战1-福报程序员的解雇清单1.3.2 系统学习Python
Python办公自动化教程-1.3节: 项目实战1-福报程序员的解雇清单1.3.2 系统学习Python
信号检测检测时间改变时检测概率_漏检_虚警概率曲线
信号检测检测时间改变时检测概率_漏检_虚警概率曲线

评论列表共有 0 条评论

立即
投稿
返回
顶部