目 录
摘 要 1
Abstract 1
1、 绪论 2
1.1 课题开发背景 2
1.1.1 图像融合的定义 2
1.1.2 手动配准与图象融合 2
1.1.3 图象融合研究的发展现状和研究热点 3
1.2 课题设计要求 4
2、MATLAB程序设计 5
2.1 MATLAB软件简介 5
2.2 MATLAB软件窗口环境 7
2.3 M语言编程 8
3、图像融合算法 9
3.1 图象融合算法的层次分类 9
3.2 图像融合规则 10
3.3 图像融合方法 11
3.4 图像融合步骤 12
4、各算法程序 13
4.1 一般方法 13
4.2 PCA算法程序 14
4.3 金字塔(Pyramid)算法程序 15
4.4 小波变换(DWT)算法程序 18
5、实验结果 22
6、图像融合的应用 24
7、总结 25
参考文献 26
摘 要
数字图像融合是以图像为主要研究内容的数据融合技术,是把多个不同模式的图像传感器获得的同一场景的多幅图像或同一传感器在不同时刻获得的同一场景的多幅图像合成为一幅图像的过程。本文首先介绍了数字图像融合的定义、发展现状和研究热点,接着论述了图像融合的规则、方法和步骤。并给出了三种融合算法程序,即PCA算法、金字塔图像融合算法与基于小波变换的算法程序,在最后论述了图像融合技术在军事、医学图像和遥感测控中的应用。
关键词:图像融合 小波变换 Matlab
Abstract
Digital image fusion is the technology of data fusion mainly study the images is the different patterns of images of the same scene sensors to the same number of sensors or images acquired at different times the same scene for a number of synthetic images images process. The first introduced digital image integration definition, the current development and research hot, and then discussed the integration of images of the rules, methods and steps. Three integration algorithms and procedures given that the PCA algorithms, pyramid image integration algorithms and algorithms based on wavelets change procedures discussed in the final image integration technology in the military, medical imaging and remote sensing, monitoring and control applications.
Keywords:Image fusion Wavelets change Matlab
- 绪论
- 课题开发背景
1.1.1 图像融合的定义
数字图像融合(Digital Image Fusion)是以图像为主要研究内容的数据融合技术,是把多个不同模式的图像传感器获得的同一场景的多幅图像或同一传感器在不同时刻获得的同一场景的多幅图像合成为一幅图像的过程。由于不同模式的图像传感器的成像机理不同,工作电磁波的波长不同,所以不同图像传感器获得的同一场景的多幅图像之间具有信息的冗余性和互补性,经图像融合技术得到的合成图像则可以更全面、更精确地描述所研究的对象。正是由于这一特点,图像融合技术现已广泛地应用于军事、遥感、计算机视觉、医学图像处理等领域中。
数字图像融合是图像分析的一项重要技术,该技术在数字地图拼接、全景图、虚拟现实等领域有着重要应用。虽然Photoshop等图像处现软件提供了图像处理功能,可以通过拖放的方式进行图像拼接,但由于完全是手工操作,单调乏味,且精度不高,因此,有必要寻找一种方便可行的图像融合方法。Matlab具有强大的计算功能和丰富的工具箱函数,例如图像处理和小波工具箱包含了大多数经典算法,并且它提供了一个非常方便快捷的算法研究平台,可让用户把精力集中在算法上而不是编程上,从而能大大提高研究效率。
1.1.2 手动配准与图象融合
图像融合包含图像配准和无缝合成两个部分.由于成像时受到各种变形因素的影响,得到的各幅图像间存在着相对的几何差异。图像配准是通过数学模拟来对图像间存在着的几何差异进行校正,把相邻两幅图像合成到同一坐标系下,并使得相同景物在不同的局部图像中对应起来,以便于图像无缝合成。本文采用Matlab中的cpselect、cp2tform函数完成几何配准。cpselect函数显示图像界面,手动在两幅图像的重叠部分选取配准控制点,Matlab自动进行亚像素分析,由cp2tform函数值正重叠部分的几何差异。Matlab中的cp2tform函数能修正6种变形,分别是图(b):线性相似;图(c):仿射;图(d):投影;图(e):多顶式;图(o:分段线性;图(g):局部加权平均。前4种为全局变换,后两种为局部变换,如图I所示,图(a)为修正结果;图(b)至图(g)为对应的变形。
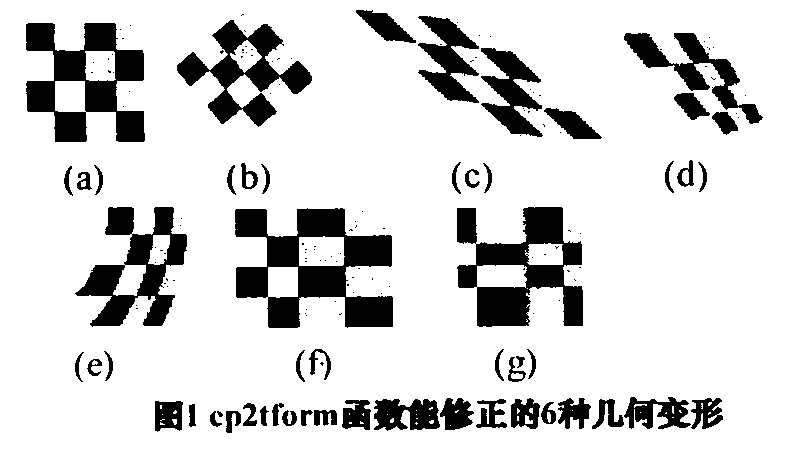
图1-1 cp2tform函数能修正的6种几何变形
图像配准之后,由于图像重叠区域之间差异的存在,如果将图像象素简单叠加,拼按处就会出现明显的拼接缝,因此需要一种技术修正待拼接图像拼接缝附近的颜色值,使之平滑过渡,实现无缝合成。传统的融合方法多是在时间域对图像进行算术运算,没有考虑处理图像时其相应频率域的变化。从数学上讲,拼接缝的消除相当于图像颜色或灰度曲面的光滑连接,但实际上图像的拼接与曲面的光滑不同,图像颜色或灰度曲面的光滑表现为对图像的模糊化,从而导致图像模糊不清。
1.1.3 图象融合研究的发展现状和研究热点
在众多的图像融合技术中,基于小波变换的图像融合方法已成为现今研究的一个热点。这类算法主要是利用人眼对局部对比度的变化比较敏感这一事实,根据一定的融合规则,在多幅原图像中选择出最显著的特征,例如边缘、线段等,并将这些特征保留在最终的合成图像中。在一幅图像的小波变换中,绝对值较大的小波系数对应于边缘这些较为显著的特征,所以大部分基于小波变换的图像融合算法主要研究如何选择合成图像中的小波系数,也就是三个方向上的高频系数,从而达到保留图像边缘的目的。虽然小波系数(高频系数)的选择对于保留图像的边缘等特征具有非常主要的作用,但尺度系数(低频系数)决定了图像的轮廓,正确地选择尺度系数对提高合成图像的视觉效果具有举足轻重的作用。
本文给出了一种基于小波变换的图像融合算法,在考虑小波系数选择规则的前提下,还重点研究了尺度系数的选择方案。小波系数的选择基于绝对值最大的原则,并对选择方案的一致性进行了验证。所谓的一致性指的是对于空间某像素点,其小波系数的选择方案应和其邻近点一致。本文设计了三种选择尺度系数的方案,并从理论上和仿真结果上对这三种方案进行了比较,选择出一种最好的方案。本文给出的算法可用于两幅图像或多幅图像的融合,从仿真结果可看出,这个算法较好地保持了图像的边缘,具有较好的视觉效果。
- 课题设计要求
题 目:几种图像融合算法的Matlab程序设计
初始条件:
- 提供实验室机房及其matlab软件;
2、提供两张同一景物不同效果的图片;
3、数字图像处理的基本理论学习。
要求完成的主要任务:(包括课程设计工作量及其技术要求,以及说明书撰写等具体要求):
(1)掌握图像融合的基本原理;
(2)熟练掌握matlab软件,并利用matlab设计一程序完成以下功能;
(3)通过对图像融合原理的认识,进行实现图像融合的程序设计;
(4)用两张灰度图片进行该程序的检验,记录其结果,并对产生的结果进行比较分析;
(5)独立完成课程设计说明书。
2、MATLAB程序设计
2.1 MATLAB软件简介
MATLAB 的名称源自 Matrix Laboratory ,它是一种科学计算软件,专门以矩阵的形式处理数据。 MATLAB 将高性能的数值计算和可视化集成在一起,并提供了大量的内置函数,从而被广泛地应用于科学计算、控制系统、信息处理等领域的分析、仿真和设计工作,而且利用 MATLAB 产品的开放式结构,可以非常容易地对 MATLAB 的功能进行扩充,从而在不断深化对问题认识的同时,不断完善 MATLAB 产品以提高产品自身的竞争能力。
目前 MATLAB 产品族可以用来进行:
| | 数值分析 |
| | 数值和符号计算 |
| | 工程与科学绘图 |
| | 控制系统的设计与方针 |
| | 数字图像处理 |
| | 数字信号处理 |
| | 通讯系统设计与仿真 |
| | 财务与金融工程 |
表2-1 MATLAB产品族
MATLAB 是 MATLAB 产品家族的基础,它提供了基本的数学算法,例如矩阵运算、数值分析算法, MATLAB 集成了 2D 和 3D 图形功能,以完成相应数值可视化的工作,并且提供了一种交互式的高级编程语言—— M 语言,利用 M 语言可以通过编写脚本或者函数文件实现用户自己的算法。
MATLAB Compiler 是一种编译工具,它能够将那些利用 MATLAB 提供的编程语言—— M 语言编写的函数文件编译生成为函数库、可执行文件 COM 组件等等。这样就可以扩展 MATLAB 功能,使 MATLAB 能够同其他高级编程语言例如 C/C++ 语言进行混合应用,取长补短,以提高程序的运行效率,丰富程序开发的手段。
利用 M 语言还开发了相应的 MATLAB 专业工具箱函数供用户直接使用。这些工具箱应用的算法是开放的可扩展的,用户不仅可以查看其中的算法,还可以针对一些算法进行修改,甚至允许开发自己的算法扩充工具箱的功能。目前 MATLAB 产品的工具箱有四十多个,分别涵盖了数据获取、科学计算、控制系统设计与分析、数字信号处理、数字图像处理、金融财务分析以及生物遗传工程等专业领域。
图2-1 MATLAB的框图设计环境
Simulink 是基于 MATLAB的框图设计环境,可以用来对各种动态系统进行建模、分析和仿真,它的建模范围广泛,可以针对任何能够用数学来描述的系统进行建模,例如航空航天动力学系统、卫星控制制导系统、通讯系统、船舶及汽车等等,其中了包括连续、离散,条件执行,事件驱动,单速率、多速率和混杂系统等等。 Simulink 提供了利用鼠标拖放的方法建立系统框图模型的图形界面,而且 Simulink 还提供了丰富的功能块以及不同的专业模块集合,利用 Simulink 几乎可以做到不书写一行代码完成整个动态系统的建模工作。
Stateflow 是一个交互式的设计工具,它基于有限状态机的理论,可以用来对复杂的事件驱动系统进行建模和仿真。 Stateflow 与 Simulink 和 MATLAB 紧密集成,可以将 Stateflow 创建的复杂控制逻辑有效地结合到 Simulink 的模型中。
在 MATLAB 产品族中,自动化的代码生成工具主要有 Real-Time Workshop ( RTW )和 Stateflow Coder ,这两种代码生成工具可以直接将 Simulink 的模型框图和 Stateflow 的状态图转换成高效优化的程序代码。利用 RTW 生成的代码简洁、可靠、易读。目前 RTW 支持生成标准的 C 语言代码,并且具备了生成其他语言代码的能力。整个代码的生成、编译以及相应的目标下载过程都是自动完成的,用户需要做得仅仅使用鼠标点击几个按钮即可。 MathWorks 公司针对不同的实时或非实时操作系统平台,开发了相应的目标选项,配合不同的软硬件系统,可以完成快速控制原型( Rapid Control Prototype )开发、硬件在回路的实时仿真( Hardware-in-Loop )、产品代码生成等工作。
另外, MATLAB 开放性的可扩充体系允许用户开发自定义的系统目标,利用 Real-Time Workshop Embedded Coder 能够直接将 Simulink 的模型转变成效率优化的产品级代码。代码不仅可以是浮点的,还可以是定点的。
图2-2 MATLAB系统开发体系
MATLAB 开放的产品体系使 MATLAB 成为了诸多领域的开发首选软件,并且, MATLAB 还具有 300 余家第三方合作伙伴,分布在科学计算、机械动力、化工、计算机通讯、汽车、金融等领域。接口方式包括了联合建模、数据共享、开发流程衔接等等。
2.2 MATLAB软件窗口环境
计算机安装好MATLAB之后,双击MATLAB图标,就可以进入命令窗口,此时意味着系统处于准备接受命令的状态,可以在命令窗口中直接输入命令语句。
MATLAB语句形式
》变量=表达式;
通过等于符号将表达式的值赋予变量。当键入回车键时,该语句被执行。语句执行之后,窗口自动显示出语句执行的结果。如果希望结果不被显示,则只要在语句之后加上一个分号(;)即可。此时尽管结果没有显示,但它依然被赋值并在MATLAB工作空间中分配了内存。
变量和数值显示格式 :
(1)变量
- 变量的命名:变量的名字必须以字母开头(不能超过19个字符),之后可以是任意字母、数字或下划线;变量名称区分字母的大小写;变量中不能包含有标点符号。
- 一些特殊的变量
ans:用于结果的缺省变量名 i、j:虚数单位
pi:圆周率 nargin:函数的输入变量个数
eps:计算机的最小数 nargout:函数的输出变量个数
inf:无穷大 realmin:最小正实数
realmax:最大正实数 nan:不定量
flops:浮点运算数
- 变量操作
在命令窗口中,同时存储着输入的命令和创建的所有变量值,它们可以在任何需要的时候被调用。如要察看变量a的值,只需要在命令窗口中输入变量的名称即可:》a
(2)数值显示格式
任何MATLAB的语句的执行结果都可以在屏幕上显示,同时赋值给指定的变量,没有指定变量时,赋值给一个特殊的变量ans,数据的显示格式由format命令控制。
format只是影响结果的显示,不影响其计算与存储;MATLAB总是以双字长浮点数(双精度)来执行所有的运算。
2.3 M语言编程
MATLAB是美国MathWorks公司开发的用于教育、工程与科学计算的软件产品,它向用户提供从概念设计、算法开发、建模仿真到实时实现的理想集成环境。无论是进行科学研究、产品开发,还是从事教育事业,MATLAB产品都是非常有效的工具。相对于其他类似于MATLAB的仿真软件,MATLAB的一个显著特点就是它提供了一种用于编程的高级语言——M语言。通过这种语言,用户可以用类似于数学公式的方式来编写算法,大大降低了编程所需的难度并节省了时间,从而让用户把主要的精力集中在算法的构思而不是编程上。
在MATLAB中,在给变量赋值之前,不需要定义它的类型。例如对变量var1赋值1000,并没有事先定义var1的数据类型。MATLAB会自动决定变量的类型,并为它分配内存空间。对上述变量var1,MATLAB将它默认定义为双精度浮点型,分配8个字节的存储空间。M语言中的变量名(包括函数名)是以英文字母开头的英文字母、下划线和阿拉伯数字的组合,有效长度不超过31。
M语言支持类似于数学公式的编程。例如,C=A+B就可完成矩阵A和矩阵B的相加运算,并把结果存储在C中。MATLAB中所有的变量都没有维数的限制(维数自动扩展),并且是以数组(array)的方式存储。但在数学意义上,基本上可以把所有的变量都当作矩阵来理解,尤其是对数值变量(对于结构数组,元胞数组最好不要当作矩阵来理解)。例如在C=A+B中,变量A和B都是以2×2维数组的方式存储的(存储方式为按列存储,而C/C++中的数组变量是按行存储的,这个区别需要注意),在数学意义上可将A和B当作两个2×2维的矩阵,C=A+B完成的便是两个矩阵的相加运算。同样的,[U,S,V]=svd(A)实现对矩阵A的奇异值分解。在MATLAB中所有变量的维数都可自动扩展,但始终保持它的矩形结构。
3、图像融合算法
3.1 图象融合算法的层次分类
图像融合系统的算法按层次结构划分可分为信号级、像素级、特征级和决策级。
信号级融合:是指合成一组传感器信号,目的是提供与原始信号形式相同但品质更高的信号。
像素级图像融合:是指直接对图像中像素点进行信息综合处理的过程像素级图像融合的日的是生成一幅包含更多信息、更清晰的图像像素级图像融合属于较低层次的融合,目前,大部分研究集中在该层次上。像素层图像融合一般要求原始图像在空间上精确配准,如果图像具有小同分辨率,在融合前需作映射处理。
特征级图像融合:是指从各个传感器图像中提取特征信息,并将其进行综合分析和处理的过程。提取的特征信息应是像素信息的充分表示量或充分统计量,典型的特征信息有边缘、形状、轮廓、角、纹理、相似亮度区域、相似景深区域等在进行融合处理时,所关心的主要特征信息的具体形式和内容与多传感器图像融合的应用目的/场合密切相关。通过特征级图像融合可以在原始图像中挖掘相关特征信息、增加特征信息的可信度、排除虚假特征、建立新的复合特征等。特征级图像融合是中间层次上的融合,为决策级融合做准备。特征级融合对传感器对准要求不如信号级和像素级要求严格,因此图像传感器可分布于不同平台上。特征级融合的优点在于可观的信息压缩,便于实时处理。由于所提出的特征直接与决策分析有关,因而融合结果能最大限度地给出决策分析所需要的特征信息。目前大多数C4I系统的数据融合研究都是在该层次上展开的。
决策级图像融合:是指对每个图像的特征信息进行分类、识别等处理,形成相应的结果后,进行进一步的融合过程最终的决策结果是全局最优决策。决策级融合是一种更高层次的信息融合,其结果将为各种控制或决策提供依据。为此,决策级融合必须结合具体的应用及需求特点,有选择地利用特征级融合所抽取或测量的有关目标的各类特征信息,才能实现决策级融合的目的,其结果将直接影响最后的决策水平。由于输入为各种特征信息,而结果为决策描述,因此决策级融合数据量最小,抗干扰能力强。决策级融合的主要优点可概括为:①通信及传输要求低,这是由其数据量少决定的;②容错性高对于一个或若十个传感器的数据干扰,可以通过适当的融合力一法予以消除;③数据要求低,传感器可以是同质或异质,对传感器的依赖性和要求降低;④分析能力强,能全力一位有效反映目标及环境的信息,满足小同应用的需要。
3.2 图像融合规则
图像的融合规则(Fusion rule)是图像融合的核心,融合规则的好坏直接影响融合图像的速度和质量。
Burt提出了基于像素选取的融合规则,在将原图像分解成不同分辨率图像的基础上,选取绝对值最大的像素值(或系数)作为融合后的像素值(或系数)。这是基于在不同分辨率图像中,具有较大值的像素(或系数)包含更多的图像信息。
Petrovic和Xydeas提出了考虑分解层内各图像(若存在多个图像)及分解层间的相关性的像素选取融合规则。蒲恬在应用小波变换进行图像融合时,根据人类视觉系统对局部对比度敏感的特性,采用了基于对比度的像素选取融合规则。
基于像素的融合选取仅是以单个像素作为融合对象,它并未考虑图像相邻像素间的相关性,因此融合结果不是很理想。考虑图像相邻像素间的相关性,Burt和Kolczynski提出了基于区域特性选择的加权平均融合规则,将像素值(或系数)的融合选取与其所在的局部区域联系起来。
在Lietal提出的融合规则中,其在选取窗口区域中较大的像素值(或系数)作为融合后像素值(或系数)的同时,还考虑了窗口区域像素(或系数)的相关性。Chibani和Houacine在其融合规则中,通过计算输入原图像相应窗口区域中像素绝对值相比较大的个数,决定融合像素的选取。基于窗口区域的融合规则由于考虑相邻像素的相关性,因此减少了融合像素的错误选取。融合效果得到提高。
ZZhang和Blum提出了基于区域的融合规则,将图像中每个像素均看作区域或边缘的一部分,并用区域和边界等图像信息来指导融合选取。采用这种融合规则所得到的融合效果较好,但此规则相对其他融合规则要复杂。对于复杂的
图像,此规则不易于实现。
3.3 图像融合方法
迄今为止,数据融合方法主要是在像元级和特征级上进行的。常用的融合方法有HIS融合法、KL变换融合法、高通滤波融合法、小波变换融合法、金字塔变换融合法、样条变换融合法等。下面简要介绍其中的几种方法。
1. HIS融合法
HIS融合法在多传感器影象像元融合方面应用较广,例如:一低分辨率三波段图象与一高分辨率单波段图象进行 融合处理。这种方法将三个波段的低分辨率的数据通过HIS变换转换到HIS空间,同时将单波段高分辨率图象进行对比度拉伸以使其灰度的均值与方差和HIS空间中亮度分量图象一致,然后将拉伸过的高分辨率图象作为新的亮度分量代入HIS反变换到原始空间中。这样获得的高分辨率彩色图象既具有较高空间分辨率,同时又具有与影象相同的色调和饱和度,有利于目视解译和计算机识别。
2. KL变换融合法
KL变换融合法又称为主成分分析法。与HIS变换法类似,它将低分辨率的图象(三个波段或更多)作为输入分量进行主成分分析,而将高分辨率图象拉伸使其具有于第一主成分相同的均值和方差,然后用拉伸后的高分辨率影象代替主成分变换的第一分量进行逆变换。高空间分辨率数据与高光谱分辨率数据通过融合得到的新的数据包含了源图象的高分辨率和高光谱分辨率特征,保留了原图象的高频信息。这样,融合图象上目标细部特征更加清晰,光谱信息更加丰富。
3. 高通滤波融合法
高通滤波融合法将高分辨率图象中的边缘信息提取出来,加入到低分辨率高光谱图象中。首先,通过高通滤波器提取高分辨率图象中的高频分量,然后将高通滤波结果加入到高光谱分辨率的图象中,形成高频特征信息突出的融合影象。
4. 小波变换融合法
利用离散的小波变换,将N幅待融合的图象的每一幅分解成M幅子图象,然后在每一级上对来自N幅待融合图象的M幅子图象进行融合,得到该级的融合图象。在得到所有M级的融合图象后,实施逆变换得到融合结果。
3.4 图像融合步骤
目前国内外己有大量图像融合技术的研究报道,不论应用何种技术方法,必须遵守的基本原则是两张或多张图像上对应的每一点都应对位准确。由于研究对象、目的不同,图像融合方法亦可多种多样,其主要步骤归纳如下:
(1) 预处理:对获取的两种图像数据进行去噪、增强等处理,统一数据格式、图像大小和分辨率。对序列断层图像作三维重建和显示,根据目标特点建立数学模型;
图3-1 图像融合步骤示意图
(2) 分割目标和选择配准特征点:在二维或三维情况下,对目标物或兴趣区进行分割。选取的特点应是同一物理标记在两个图像上的对应点,该物理标记可以是人工标记,也可以是人体解剖特征点;
(3 )利用特征点进行图像配准:可视作两个数据集间的线性或非线性变换,使变换后的两个数据集的误差达到某种准则的最小值;
(4) 融合图像创建:配准后的两种模式的图像在同一坐标系下将各自的有用信息融合表达成二维或三维图像;
(5) 参数提取:从融合图像中提取和测量特征参数,定性、定量分析。
4、各算法程序
4.1 一般方法
图像融合是通过一个数学模型把来自不同传感器的多幅图像综合成一幅满足特定应用需求的图像的过程,从而可以有效地把不同图像传感器的优点结合起来,提高对图像信息分析和提取的能力。简单的图像融合方法不对参加融合的源图像进行任何变换和分解,而是直接对源图像中的各对应像素分别进行选择、平均或加权平均、多元回归或其它数学运算等处理后,最终合成一幅融合图像。
对于图像融合的对象,可以分为两大类,即多光谱图像(通常为RGB彩色图像)与灰度图像之间的融合,以及灰度图像之间的融合。灰度图像之间的融合,在大体上可分为三大类。一类是简单融合方法,包括将空间对准的两幅图像直接求加权平均值。另一类方法是基于金字塔形分解和重建算法的融合方法,主要包括梯度金字塔法、对比度和比率金字塔法以及拉普拉斯金字塔法等,它们首先构造输入图像的金字塔,再按一定的特征选择方法取值形成融合金字塔,通过对金字塔实施逆变换进行图像重建,最终生成融合图像,它们的融合效果要远优于第一类方法,然而它也有很多不尽如人意的地方。还有一类方法就是近几年兴起的基于小波变换的图像融合方法,它通常采用多分辨分析和Mallat快速算法,通过在各层的特征域上进行有针对性的融合,比较容易提取原始图像的结构信息和细节信息,所以融合效果要好于基于金字塔形变换的图像融合法。这是因为小波变换更为紧凑;小波表达式提供了方向信息,而金字塔表达式未将空间方向选择性引入分解过程;由于可以选择正交小波核,因此不同分辨率包含的信息是唯一的,而金字塔分解在两个不同的尺度之间含有冗余,另外金字塔不同级的数据相关,很难知道两级之间的相似性是由于冗余还是图像本身的性质引起的;金字塔的重构过程可能具有不稳定性,特别是两幅图像存在明显差异区域时,融合图像会出现斑块,而小波变换图像融合则没有类似的问题。此外,小波变换具有完善重建能力保证了信号在分解重构过程中没有信息损失和信息冗余产生。
4.2 PCA算法程序
基于PCA的图像融合:又称K-L变换法,它的几何意义是把原始特征空间的特征轴旋转到平行于混合集群结构轴的方向去,得到新的特征轴。实际操作是将原来的各个因素指标(这些指标中部分有相关关系)重新组合,组合后的新指标是互不相关的。在由这些新指标组成的新特征轴中,只用前几个分量图像就能完全表征原始集群的有效信息,图像中彼此相关的数据被压缩,而特征得到了突出,此方法在对于具有相关因子的多源遥感数据进行融合时具有显著优势。
基于PCA的融合算法程序:
function Y = fuse_pca(M1, M2)
%Y = fuse_pca(M1, M2) image fusion with PCA method
%
% M1 - input image #1
% M2 - input image #2
%
% Y - fused image
% (Oliver Rockinger 16.08.99)
% check inputs
[z1 s1] = size(M1);
[z2 s2] = size(M2);
if (z1 ~= z2) | (s1 ~= s2)
error('Input images are not of same size');
end;
% compute, select & normalize eigenvalues
[V, D] = eig(cov([M1(:) M2(:)]));
if (D(1,1) > D(2,2))
a = V(:,1)./sum(V(:,1));
else
a = V(:,2)./sum(V(:,2));
end;
% and fuse
Y = a(1)*M1+a(2)*M2;
4.3 金字塔(Pyramid)算法程序
金字塔图像融合法:用金字塔在空间上表示图像是一种简单方便的方法。概括地说金字塔图像融合法就是将参加融合的每幅源图像作金字塔表示,将所有图像的金字塔表示在各相应层上以一定的融合规则融合,可得到合成的金字塔。将合成的金字塔,用金字塔生成的逆过程重构图像,则可得到融合图像。金字塔可分为:Laplacian金字塔、Gaussian金字塔、梯度金字塔、数学形态金字塔等。
基于FSD Pyramid的图像融合算法程序:
function Y = fuse_fsd(M1, M2, zt, ap, mp)
%Y = fuse_fsd(M1, M2, zt, ap, mp) image fusion with fsd pyramid
%
% M1 - input image A
% M2 - input image B
% zt - maximum decomposition level
% ap - coefficient selection highpass (see selc.m)
% mp - coefficient selection base image (see selb.m)
%
% Y - fused image
% (Oliver Rockinger 16.08.99)
% check inputs
[z1 s1] = size(M1);
[z2 s2] = size(M2);
if (z1 ~= z2) | (s1 ~= s2)
error('Input images are not of same size');
end;
% define filter
w = [1 4 6 4 1] / 16;
% cells for selected images
E = cell(1,zt);
% loop over decomposition depth -> analysis
for i1 = 1:zt
% calculate and store actual image size
[z s] = size(M1);
zl(i1) = z; sl(i1) = s;
% check if image expansion necessary
if (floor(z/2) ~= z/2), ew(1) = 1; else, ew(1) = 0; end;
if (floor(s/2) ~= s/2), ew(2) = 1; else, ew(2) = 0; end;
% perform expansion if necessary
if (any(ew))
M1 = adb(M1,ew);
M2 = adb(M2,ew);
end;
% perform filtering
G1 = conv2(conv2(es2(M1,2), w, 'valid'),w', 'valid');
G2 = conv2(conv2(es2(M2,2), w, 'valid'),w', 'valid');
% select coefficients and store them
E(i1) = {selc(M1-G1, M2-G2, ap)};
% decimate
M1 = dec2(G1);
M2 = dec2(G2);
end;
% select base coefficients of last decompostion stage
M1 = selb(M1,M2,mp);
% loop over decomposition depth -> synthesis
for i1 = zt:-1:1
% undecimate and interpolate
M1T = conv2(conv2(es2(undec2(M1), 2), 2*w, 'valid'), 2*w', 'valid');
% add coefficients
M1 = M1T + E{i1};
% select valid image region
M1 = M1(1:zl(i1),1:sl(i1));
end;
% copy image
Y = M1;
4.4 小波变换(DWT)算法程序
在众多的图像融合技术中,基于小波变换的图像融合方法已成为现今研究的一个热点。这类算法主要是利用人眼对局部对比度的变化比较敏感这一事实,根据一定的融合规则,在多幅原图像中选择出最显著的特征,例如边缘、线段等,并将这些特征保留在最终的合成图像中。在一幅图像的小波变换中,绝对值较大的小波系数对应于边缘这些较为显著的特征,所以大部分基于小波变换的图像融合算法主要研究如何选择合成图像中的小波系数,也就是三个方向上的高频系数,从而达到保留图像边缘的目的。虽然小波系数(高频系数)的选择对于保留图像的边缘等特征具有非常主要的作用,但尺度系数(低频系数)决定了图像的轮廓,正确地选择尺度系数对提高合成图像的视觉效果具有举足轻重的作用。
基于SIDWT(Shift Invariance Discrete Wavelet Transform)小波变换的算法程序:
function Y = fuse_sih(M1, M2, zt, ap, mp)
%Y = fuse_sih(M1, M2, zt, ap, mp) image fusion with SIDWT, Wavelet is Haar
%
% M1 - input image A
% M2 - input image B
% zt - maximum decomposition level
% ap - coefficient selection highpass (see selc.m)
% mp - coefficient selection base image (see selb.m)
%
% Y - fused image
% (Oliver Rockinger 16.08.99)
% check inputs
[z1 s1] = size(M1);
[z2 s2] = size(M2);
if (z1 ~= z2) | (s1 ~= s2)
error('Input images are not of same size');
end;
% cells for selected images
E = cell(3,zt);
% loop over decomposition depth -> analysis
for i1 = 1:zt
% calculate and store actual image size
[z s] = size(M1);
zl(i1) = z; sl(i1) = s;
% define actual filters (inserting zeros between coefficients)
h1 = [zeros(1,floor(2^(i1-2))), 0.5, zeros(1,floor(2^(i1-1)-1)), 0.5, zeros(1,max([floor(2^(i1-2)),1]))];
g1 = [zeros(1,floor(2^(i1-2))), 0.5, zeros(1,floor(2^(i1-1)-1)), -0.5, zeros(1,max([floor(2^(i1-2)),1]))];
fh = floor(length(h1)/2);
% image A
Z1 = conv2(es(M1, fh, 1), g1, 'valid');
A1 = conv2(es(Z1, fh, 2), g1','valid');
A2 = conv2(es(Z1, fh, 2), h1','valid');
Z1 = conv2(es(M1, fh, 1), h1, 'valid');
A3 = conv2(es(Z1, fh, 2), g1','valid');
A4 = conv2(es(Z1, fh, 2), h1','valid');
% image B
Z1 = conv2(es(M2, fh, 1), g1, 'valid');
B1 = conv2(es(Z1, fh, 2), g1','valid');
B2 = conv2(es(Z1, fh, 2), h1','valid');
Z1 = conv2(es(M2, fh, 1), h1, 'valid');
B3 = conv2(es(Z1, fh, 2), g1','valid');
B4 = conv2(es(Z1, fh, 2), h1','valid');
% select coefficients and store them
E(1,i1) = {selc(A1, B1, ap)};
E(2,i1) = {selc(A2, B2, ap)};
E(3,i1) = {selc(A3, B3, ap)};
% copy input image for next decomposition stage
M1 = A4;
M2 = B4;
end;
% select base coefficients of last decompostion stage
A4 = selb(A4,B4,mp);
% loop over decomposition depth -> synthesis
for i1 = zt:-1:1
% define actual filters (inserting zeros between coefficients)
h2 = fliplr([zeros(1,floor(2^(i1-2))), 0.5, zeros(1,floor(2^(i1-1)-1)), 0.5, zeros(1,max([floor(2^(i1-2)),1]))]);
g2 = fliplr([zeros(1,floor(2^(i1-2))), 0.5, zeros(1,floor(2^(i1-1)-1)), -0.5, zeros(1,max([floor(2^(i1-2)),1]))]);
fh = floor(length(h2)/2);
% filter (rows)
A4 = conv2(es(A4, fh, 2), h2', 'valid');
A3 = conv2(es(E{3,i1}, fh, 2), g2', 'valid');
A2 = conv2(es(E{2,i1}, fh, 2), h2', 'valid');
A1 = conv2(es(E{1,i1}, fh, 2), g2', 'valid');
% filter (columns)
A4 = conv2(es(A4+A3, fh, 1), h2, 'valid');
A2 = conv2(es(A2+A1, fh, 1), g2, 'valid');
% add images
A4 = A4 + A2;
end;
% copy image
Y = A4;
5、实验结果
下面将本文的算法用于多聚焦图像的融合。多聚焦图像指的是对相同的场景用不同的焦距进行拍摄,得到镜头聚焦目标不同的多个图像。经过图像融合技术后,就可以得到一个所有目标都聚焦清晰的图像。图5-1中左边的目标较为清晰,图5-2中右边的目标较为清晰。

图5-1 聚焦在左边的图像

图5-2 聚焦在右边的图像
我们分别利用基于PCA的算法、金字塔图像融合法和小波变换法的算法程序得到的的融合图像结果,如图5-3、图5-4、图5-5所示

图5-3 基于PCA算法的融合图像

图5-4 基于金字塔图像融合算法的融合图像

图5-5 基于SIDWT小波变换的融合图像
从实验结果可以看出,三种方案都可以得到较满意的视觉效果,消除了原图像的聚焦差异,提高了图像的清晰度,在合成图像中左、右两边的目标都很清晰。但通过比较分析,我们可以看出基于小波变换的融合图像(图5-5)最为清晰,所表现的图像细节效果最好,重影现象消除得最干净。图5-3的清晰度不够,而图5-4的细节表现力较弱,只有图5-5的边缘最清晰,重影消除地最干净,细节得到了最好地保留。
6、图像融合的应用
图像融合技术在军事、遥感和医学成像等领域有着广泛的应用,和人工智能等的新兴技术。近年来,图像融合已成为一种十分重要的图像分析与计算机视觉技术。它在自动目标识别计算机视觉!遥感、机器人、医学图像处理以及军事应用等领域有着广泛的应用前景。
智能机器人领域:动作控制"对环境的视觉触觉力矩反馈"立体摄像融合"智能注视控制"自动目标识别和跟踪。信息融合技术对机器人领域起到了一定的推动作用。作为信息融合的重要分支-图像融合技术可用于自动目标识别等。
医学影像领域:计算机辅助手术、3-D表面空间校准。医学图像融合是医学图像后处理的研究热点主要包括转换&配准和信息提取三个步骤。它充分利用多模式图像获得互补信息,使临床的诊断和治疗更加准确完善。
制造业领域:电子线路和部件检查&产品表面测量和检验&材料探伤&生产过程监视&复杂设备诊断。
战场和司法领域:陆海空目标/事件的检测跟踪和识别&隐蔽武器的探测&战场监视&夜间飞行导航。
在遥感领域中,电磁光谱应用、黑白空中摄影到多光谱主动微波空间成像雷达、基于摄像方法和数字方法的融合技术等。
7、总结
数字图像融合是图像分析的一项重要技术,该技术在数字地图拼接、全景图、虚拟现实等领域有着重要应用。虽然Photoshop等图像处现软件提供了图像处理功能,可以通过拖放的方式进行图像拼接,但由于完全是手工操作,单调乏味,且精度不高,因此,有必要寻找一种方便可行的图像融合方法。Mattab具有强大的计算功能和丰富的工具箱函数,例如图像处理和小波工具箱包含了大多数经典算法,并且它提供了一个非常方便快捷的算法研究平台,可让用户把精力集中在算法上而不是编程上,从而能大大提高研究效率。
本文给出了几种不同的图像融合方法,并介绍了图像融合的规则、方法和步骤。并给出了三种常用的融合算法程序,在最后论述了图像融合技术在军事、医学图像和遥感测控中的应用。
三种融合算法的方案,即PCA算法、金字塔图像融合算法与基于小波变换算法。PCA算法在一定程度上降低了图像的对比度,金字塔图像融合算法在平均法的基础上有一定的改善,但并没有非常明显的提高;第三种方法则利用小波变换算法对原图像进行融合处理,边缘的点加以保留,所以得到的合成图像最清晰,细节最丰富。最后本文将这一算法用于多聚焦图像的融合。从仿真结果可以看出,第三种方案的融合效果最好。
参考文献
1、数字图象处理:MATLAB版:using MATLAB (美) Rafael C.Gonzalez, Richard E. Woods, Steven L. Eddins著;阮秋琦等译 北京:电子工业出版社,2005
2、数字图象处理与分析基础 黄爱民, 安向京, 骆力等编著 北京:中国水利水电出版社,2005
3、数字图象处理导论 赵荣椿,赵忠明,崔甦生编著 西安:西北工业大学出版社,1995
4、MATLAB 6.1基础及应用技巧 李海涛, 邓樱编著 北京:国防工业出版社,2002
5、MATLAB 6.5辅助图像处理 飞思科技产品研发中心编著 北京:电子工业出版社,2003
6、Matlab工具箱应用指南.控制工程篇 徐昕, 李涛, 伯晓晨等编著 北京:电子工业出版社,2000
7、Matlab信号处理与应用 董长虹主编 北京:国防工业出版社,2015
8、数字图像处理学:活用Matlab 缪绍纲编著 成都:西南交通大学出版社,2011
9、数字图像处理 (美) Rafael C. Gonzalez, Richard E. Woods著;阮秋琦, 阮宇智等译 北京:电子工业出版社,2013
10、图象处理与分析:数学形态学方法及应用 崔屹编著 北京:科学出版社,2010
最后
以上就是幸福盼望最近收集整理的关于MATLAB小波图像融合处理的全部内容,更多相关MATLAB小波图像融合处理内容请搜索靠谱客的其他文章。








发表评论 取消回复