前言：
因为工作需要开始学习车辆横纵向控制，然后学到了LQR，正好写一个博客把程序保存下来。为了加强C++代码能力，本次仿真的所有文件均用C++完成。
代码结构梳理
开始之前非常感谢这位大佬给出的参考：【自动驾驶】LQR实现轨迹跟踪，这次项目大部分都是将该博客从python翻译成C++，当然其中也发现了一些问题，后续再谈。
该项目用多个模块组成，分别为LQR、LQR_node、tool、trajectory、matplot5个模块。
1.LQR_node为主函数节点，负责调用轨迹生成模块、LQR控制器模块和画图；
2.LQR为LQR控制器模块，控制器中构造了模型参数A、B，计算黎卡提方程等功能；
3.trajectory为轨迹生成模块，并且计算出坐标点对应的曲率值；
4.tool为工具模块，定义了项目中需要的数据类型和一些角度处理函数（虽然没用到）；
5.matplot为画图模块，调用了python的matplot功能进行作图；
该项目用到的库有Eigen、python、matplotlibcpp，其中最为重要的是Eigen库，建议提前看一下该库的基本命令。
准备工作
1.项目配置Eigen库：
安装和使用C++线性代数库eigen（Windows下minGW+VS code, VS2019配置方式）
2.项目配置matplot库：
VS C++调用python进行画图matplotlib
windows下配置C++版本的matplotlib绘图工具matplotlibcpp
别忘了把解决方案配置换成Release，我在这里卡了好久
代码
1.tool.h
复制代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27#pragma once #include <iostream> using namespace std; #define pi acos(-1) //定义路径点 typedef struct waypoint { int ID; double x, y, yaw, K;//x,y,yaw,曲率K }waypoint; //定义小车状态 typedef struct vehicleState { double x, y, yaw, v, kesi;//x,y,yaw,前轮偏角kesi }vehicleState; //定义控制量 typedef struct U { double v; double kesi;//速度v,前轮偏角kesi }U; double normalize_angle(double angle);//角度归一化 [-pi,pi]; double limit_kesi(double kesi);//前轮转角限幅 [-pi/2,pi/2];
2.tool.cpp
复制代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23#include<iostream> #include<tool.h> double normalize_angle(double angle)//角度归一化 [-pi,pi]; { if (angle > pi) { angle -= 2.0 * pi; } if (angle <= -pi) { angle += 2.0 * pi; } return angle; } double limit_kesi(double kesi) { if (kesi > pi / 2) { kesi = pi / 2; } if (kesi < -pi / 2) { kesi = -pi / 2; } return kesi; }
3.LQR.h
复制代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43#include <iostream> #include <Eigen/Dense> #include "tool.h" using namespace std; typedef Eigen::Matrix<double, 3, 3> Matrix3x3; typedef Eigen::Matrix<double, 3, 1> Matrix3x1; typedef Eigen::Matrix<double, 2, 1> Matrix2x1; typedef Eigen::Matrix<double, 2, 2> Matrix2x2; typedef Eigen::Matrix<double, 3, 2> Matrix3x2; typedef Eigen::Matrix<double, 2, 3> Matrix2x3; //状态方程变量: X = [x_e y_e yaw_e]^T //状态方程控制输入: U = [v_e kesi_e]^T class LQR { private: Matrix3x3 A_d; Matrix3x2 B_d; Matrix3x3 Q; Matrix2x2 R; Matrix3x1 X_e; Matrix2x1 U_e; double L;//车辆轴距 double T;//采样间隔 double x_car, y_car, yaw_car, x_d, y_d, yaw_d;//车辆位姿和目标点位姿 double v_d, kesi_d;//期望速度和前轮偏角 double Q3[3];//Q权重，三项 double R2[2];//R权重，两项 int temp = 0; public: void initial(double L_, double T_, vehicleState car, waypoint waypoint, U U_r, double* Q_, double* R_);//初始化 void param_struct();//构造状态方程参数 Matrix2x3 cal_Riccati();//黎卡提方程求解 U cal_vel();//LQR控制器计算速度 void test(); };
4.LQR.cpp
复制代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102#include <iostream> #include <LQR.h> using namespace std; void LQR::initial(double L_, double T_, vehicleState car, waypoint waypoint, U U_r, double *Q_, double *R_) { L = L_; T = T_; x_car = car.x; y_car = car.y; yaw_car = car.yaw; x_d = waypoint.x; y_d = waypoint.y; yaw_d = waypoint.yaw; v_d = U_r.v;kesi_d = U_r.kesi; for (int i = 0; i < 3; i++) { Q3[i] = Q_[i]; } for (int j = 0; j < 2; j++) { R2[j] = R_[j]; } } void LQR::param_struct() { Q << Q3[0], 0.0, 0.0, 0.0, Q3[1], 0.0, 0.0, 0.0, Q3[2]; //cout << "Q矩阵为：n" << Q << endl; R << R2[0], 0.0, 0.0, R2[1]; //cout << "R矩阵为：n" << R << endl; A_d << 1.0, 0.0, -v_d * T * sin(yaw_d), 0.0, 1.0, v_d* T* cos(yaw_d), 0.0, 0.0, 1.0; //cout << "A_d矩阵为:n" << A_d << endl; B_d << T * cos(yaw_d), 0.0, T* sin(yaw_d), 0.0, T* tan(kesi_d)/L, v_d* T / (L * cos(kesi_d) * cos(kesi_d)); //cout << "B_d矩阵为:n" << B_d << endl; X_e << x_car - x_d, y_car - y_d, yaw_car - yaw_d; cout << "X_e矩阵为:n" << X_e << endl; } Matrix2x3 LQR::cal_Riccati() { int N = 150;//迭代终止次数 double err = 100;//误差值 double err_tolerance = 0.01;//误差收敛阈值 Matrix3x3 Qf = Q; Matrix3x3 P = Qf;//迭代初始值 //cout << "P初始矩阵为n" << P << endl; Matrix3x3 Pn;//计算的最新P矩阵 for (int iter_num = 0; iter_num < N; iter_num++) { Pn = Q + A_d.transpose() * P * A_d - A_d.transpose() * P * B_d * (R + B_d.transpose() * P * B_d).inverse() * B_d.transpose() * P * A_d;//迭代公式 //cout << "收敛误差为" << (Pn - P).array().abs().maxCoeff() << endl; //err = (Pn - P).array().abs().maxCoeff();// err = (Pn - P).lpNorm<Eigen::Infinity>(); if(err < err_tolerance)// { P = Pn; cout << "迭代次数" << iter_num << endl; break; } P = Pn; } //cout << "P矩阵为n" << P << endl; //P = Q; Matrix2x3 K = -(R + B_d.transpose() * P * B_d).inverse() * B_d.transpose() * P * A_d;//反馈率K return K; } U LQR::cal_vel() { U output; param_struct(); Matrix2x3 K = cal_Riccati(); Matrix2x1 U = K * X_e; //cout << "反馈增益K为：n" << K << endl; //cout << "控制输入U为：n" << U << endl; output.v = U[0] + v_d; output.kesi = U[1] + kesi_d; return output; } void LQR::test() //控制器效果测试 { /*param_struct(); while (temp < 1000) { Matrix2x3 K = cal_Riccati(); Matrix2x1 U = K * X_e; //cout <<"state variable is:n" <<X_e << endl; //cout <<"control input is:n"<< U << endl; Matrix3x1 X_e_ = A_d * X_e + B_d * U; X_e = X_e_; temp++; }*/ Matrix3x3 C,D,F; C << 1.0, 0.0, 0.0, 0.0, 1.0, 0.0, 0.0, 0.0, 1.0; F << 1.0, 0.0, 0.0, 0.0, 4.0, 0.0, 0.0, 0.0, 7.0; D = (C - F); double BBBB = D.lpNorm<Eigen::Infinity>(); cout << BBBB << endl; }
5.trajectory.h
复制代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18#include <iostream> #include <vector> #include "tool.h" using namespace std; class trajectory { private: vector<waypoint> waypoints; public: //set reference trajectory void refer_path(); vector<waypoint> get_path(); };
6.trajectory.cpp
复制代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50#include <iostream> #include <vector> #include <trajectory.h> #include <math.h> using namespace std; void trajectory::refer_path() { waypoint PP; for (int i = 0; i < 1000; i++) { PP.ID = i; PP.x = 0.1 * i;//x PP.y = 2.0 * sin(PP.x / 5.0) + 2.0 * cos(PP.x / 2.5);//y //直线 //PP.y = 5.5; PP.yaw = PP.K = 0.0; waypoints.push_back(PP); } for (int j = 0; j < waypoints.size(); j++) { //差分法求一阶导和二阶导 double dx, dy, ddx, ddy; if (j == 0) { dx = waypoints[1].x - waypoints[0].x; dy = waypoints[1].y - waypoints[0].y; ddx = waypoints[2].x + waypoints[0].x - 2 * waypoints[1].x; ddy = waypoints[2].y + waypoints[0].y - 2 * waypoints[1].y; } else if (j == (waypoints.size() - 1)) { dx = waypoints[j].x - waypoints[j - 1].x; dy = waypoints[j].y - waypoints[j - 1].y; ddx = waypoints[j].x + waypoints[j - 2].x - 2 * waypoints[j].x; ddy = waypoints[j].y + waypoints[j - 2].y - 2 * waypoints[j].y; } else { dx = waypoints[j + 1].x - waypoints[j].x; dy = waypoints[j + 1].y - waypoints[j].y; ddx = waypoints[j + 1].x + waypoints[j - 1].x - 2 * waypoints[j].x; ddy = waypoints[j + 1].y + waypoints[j - 1].y - 2 * waypoints[j].y; } waypoints[j].yaw = atan2(dy, dx);//yaw //计算曲率：设曲线r(t) =(x(t),y(t)),则曲率k=(x'y" - x"y')/((x')^2 + (y')^2)^(3/2). double AAA = sqrt(pow((pow(dx, 2) + pow(dy, 2)), 3)); waypoints[j].K = (ddy * dx - ddx * dy) / (sqrt(pow((pow(dx, 2) + pow(dy, 2)), 3))); } } vector<waypoint> trajectory::get_path() { return waypoints; }
7.matplotlibcpp.h
这个配置matplot库的时候会有这个头文件，代码里面直接调用就可以画图啦。
8.LQR_node.cpp
复制代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
235
236
237
238
239
240
241
242
243
244
245
246
247
248
249
250
251
252
253
254
255
256
257
258
259
260
261
262
263
264
265
266
267
268
269
270
271
272// _ooOoo_ // o8888888o // 88" . "88 // (| -_- |) // O = /O // ____/`---'____ // . ' \| |// `. // / \||| : |||// // / _||||| -:- |||||- // | | \ - /// | | // | _| ''---/'' | | // .-__ `-` ___/-. / // ___`. .' /--.-- `. . __ // ."" '< `.____<|>_/___.' >'"". // | | : `- `.;` _ /`;.`/ - ` : | | // `-. _ __ /__ _/ .-` / / // ======`-.____`-.________/___.-`____.-'====== // `=---=' // // ............................................. // 佛祖保佑 永无BUG // 佛曰: // 写字楼里写字间，写字间里程序员； // 程序人员写程序，又拿程序换酒钱。 // 酒醒只在网上坐，酒醉还来网下眠； // 酒醉酒醒日复日，网上网下年复年。 // 但愿老死电脑间，不愿鞠躬老板前； // 奔驰宝马贵者趣，公交自行程序员。 // 别人笑我忒疯癫，我笑自己命太贱； // 不见满街漂亮妹，哪个归得程序员？ #include <iostream> #include <LQR.h> #include <vector> #include <trajectory.h> #include <stdlib.h> #include "matplotlibcpp.h" using namespace std; namespace plt = matplotlibcpp; #define pi acos(-1) #define T 0.05//采样时间 很有意思的测试数据：T=0.5s，允许误差范围为±5.0m；T=0.1s，允许误差范围为±10.0m；T=0.05s；允许误差范围为±11m #define L 0.5//车辆轴距 #define V_DESIRED 0.5//期望速度 vehicleState update_state(U control, vehicleState car) { car.v = control.v; car.kesi = control.kesi; car.x += car.v * cos(car.yaw) * T; car.y += car.v * sin(car.yaw) * T; car.yaw += car.v / L * tan(car.kesi) * T; //car.yaw = normalize_angle(car.yaw); return car; } class Path { private: vector<waypoint> path; public: //添加新的路径点 void Add_new_point(waypoint& p) { path.push_back(p); } void Add_new_point(vector<waypoint>& p) { path = p; } //路径点个数 unsigned int Size() { return path.size(); } //获取路径点 waypoint Get_waypoint(int index) { waypoint p; p.ID = path[index].ID; p.x = path[index].x; p.y = path[index].y; p.yaw = path[index].yaw; p.K = path[index].K; return p; } // 搜索路径点, 将小车到起始点的距离与小车到每一个点的距离对比，找出最近的目标点索引值 int Find_target_index(vehicleState state) { double min = abs(sqrt(pow(state.x - path[0].x, 2) + pow(state.y - path[0].y, 2))); int index = 0; for (int i = 0; i < path.size(); i++) { double d = abs(sqrt(pow(state.x - path[i].x, 2) + pow(state.y - path[i].y, 2))); if (d < min) { min = d; index = i; } } //索引到终点前，当（机器人与下一个目标点的距离Lf）小于（当前目标点到下一个目标点距离L)时，索引下一个目标点 if ((index + 1) < path.size()) { double current_x = path[index].x; double current_y = path[index].y; double next_x = path[index + 1].x; double next_y = path[index + 1].y; double L_ = abs(sqrt(pow(next_x - current_x, 2) + pow(next_y - current_y, 2))); double L_1 = abs(sqrt(pow(state.x - next_x, 2) + pow(state.y - next_y, 2))); //ROS_INFO("L is %f,Lf is %f",L,Lf); if (L_1 < L_) { index += 1; } } return index; } }; class LQR_node { private: vehicleState car;//小车状态 double Q[3]; double R[2]; int lastIndex;//最后一个点索引值 waypoint lastPoint;//最后一个点信息 vector<double> x,y,x_p,y_p,v_a,v_d,kesi_a,kesi_d; public: LQR* controller = new LQR(); Path* path = new Path(); trajectory* trajec = new trajectory(); LQR_node()//初始化中添加轨迹、小车初始位姿 { //ROS: addpointcallback(); //robot: car.x = -1.325; car.y = 2.562; car.yaw = 0.964; car.v = 0.0; car.kesi = 0.1; } ~LQR_node() { free(controller); free(path); free(trajec); } void addpointcallback(){ trajec->refer_path(); vector<waypoint> waypoints = trajec->get_path(); path->Add_new_point(waypoints); cout << "path size is:" << path->Size() << endl; lastIndex = path->Size() - 1; lastPoint = path->Get_waypoint(lastIndex); } double slow_judge(double distance) { if (distance>=5.0&&distance <= 15.0) { return 0.35; } else if (distance>=0.1&&distance < 5.0) { return 0.15; } else if (distance < 0.1) { printf("reach goal!n"); plot_(); } else { return V_DESIRED; } } //控制器流程 void LQR_track() { U U_r; waypoint Point; //搜索路径点 int target_index = path->Find_target_index(car); printf("target index is : %dn", target_index); //获取路径点信息，构造期望控制量 Point = path->Get_waypoint(target_index); //printf("waypoint information is x:%f,y:%f,yaw:%f,K:%fn", Point.x, Point.y, Point.yaw, Point.K); //减速判断 double kesi = atan2(L * Point.K, 1); double v_distance = abs(sqrt(pow(car.x - lastPoint.x, 2) + pow(car.y - lastPoint.y, 2))); printf("the distance is %fn", v_distance); U_r.v = slow_judge(v_distance);U_r.kesi = kesi; printf("the desired v is: %f,the desired kesi is: %fn", U_r.v,U_r.kesi); //权重矩阵 Q[0] = 1.0; Q[1] = 1.0; Q[2] = 1.0; R[0] = 4.0; R[1] = 4.0; //使用LQR控制器 controller->initial(L, T, car, Point, U_r, Q, R);//初始化控制器 U control = controller->cal_vel();//计算输入[v, kesi] printf("the speed is: %f,the kesi is: %fn", control.v, control.kesi); printf("the car position is x: %f, y: %fn", car.x, car.y); //储存小车位姿用来画图 x.push_back(car.x); y.push_back(car.y); v_a.push_back(car.v); v_d.push_back(U_r.v); kesi_a.push_back(car.kesi); kesi_d.push_back(U_r.kesi); //小车位姿状态更新 car = update_state(control, car); } //控制启停函数 void control() { int i = 0; while (i < 10000) { LQR_track(); i++; } } //画图程序 void plot_() { vector<double> time; for (int i = 0; i < path->Size(); i++) { x_p.push_back(path->Get_waypoint(i).x); y_p.push_back(path->Get_waypoint(i).y); } for (int j = 0; j < v_a.size(); j++) { time.push_back(double(j)); } plt::subplot(3, 1, 1); plt::title("Car position"); plt::plot(x_p, y_p, "-k", x, y, "-.r"); plt::subplot(3, 1, 2); plt::title("Car speed"); plt::plot(time, v_d, "-k", time, v_a, "-.r"); plt::subplot(3, 1, 3); plt::title("Car kesi"); plt::plot(time, kesi_d, "-k", time, kesi_a, "-.r"); plt::show(); exit(0); } }; int main(char argc, char* argv) { LQR_node* node = new LQR_node(); node->control(); return 0; }
仿真测试结果：
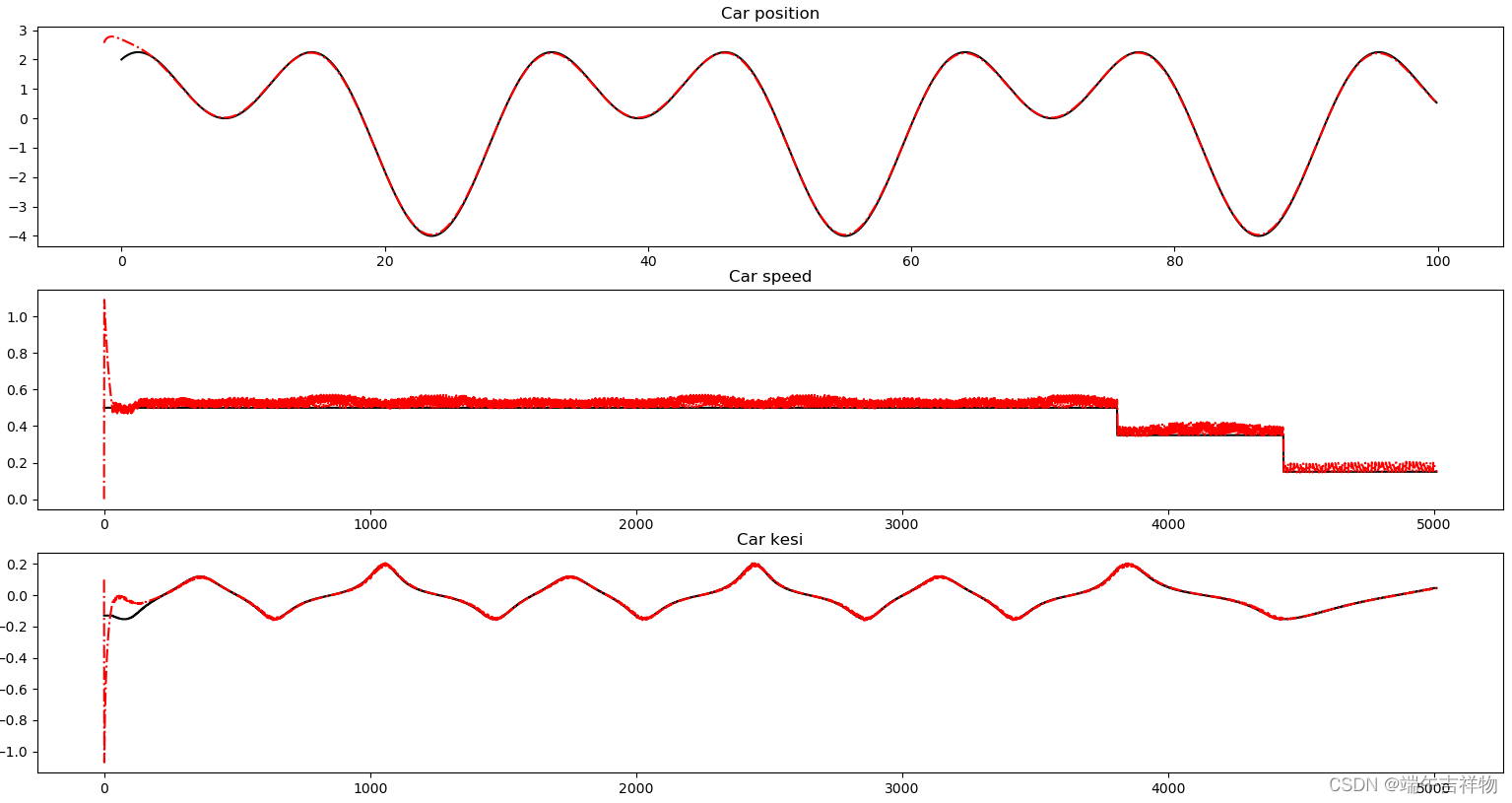
三幅图分别为车辆位置、车辆速度、车辆前轮转角。黑色实线为期望值，红色虚线为实际值。速度为0.5，后面有减速处理，可以看到效果还是挺不错的。
重要的说明！！
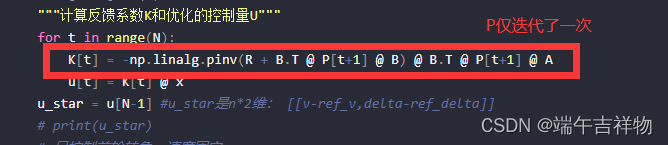
1、解黎卡提方程的问题
在大佬python版本中发现了一个问题，经过解黎卡提方程后，得到的矩阵K只迭代了一次(如下图)，这个地方我想了挺久的，最后还是按照迭代法求黎卡提（Riccati）方程的解这篇博客来解的，判定收敛的条件是无穷范数。
2.初始误差的选择(小车与轨迹起点的距离)
在调试过程中发现了一个很有意思的现象，采样时间与允许初始误差范围有关系，太大的初始误差可能会导致跟踪失败，仿真的期望速度为0.5m/s：
| 采样时间(s) | 允许初始误差范围(m) |
| 0.5 | ±5.0 |
| 0.1 | ±10.0 |
| 0.05 | ±11.0 |
测试了三种调试频率，2Hz，10Hz，20Hz，在实验平台上一般使用20Hz的，不过取极限初始误差意义不是很大，自动驾驶里面不可能在离车辆11m的地方开始规划路径。。。但还是可以测试控制器极限性能。
3.权重的选择
这个问题我调了很久，最后发现Q权重一定要比R小，不然速度就会提前计算到0，或者前轮转角值异常。我也不知道是怎么回事，相同的控制率算法写到python里面没有问题，C++有问题，就令我很费解。
4.完整代码
完整代码请见：LQR_cpp
5.后续工作
过几天会把这个项目弄到实验平台上进行仿真和实验。
最后
以上就是清爽小兔子最近收集整理的关于Visual studio C++：LQR轨迹跟踪仿真前言：代码结构梳理准备工作代码仿真测试结果： 重要的说明！！的全部内容，更多相关Visual内容请搜索靠谱客的其他文章。
本图文内容来源于网友提供，作为学习参考使用，或来自网络收集整理，版权属于原作者所有。
发表评论 取消回复