摘要：

我们讨论了用于分类的持续学习(CL)问题的一般公式——一个学习任务，其中流向学习者提供样本，学习者的目标是根据它接收到的样本，不断升级其关于旧类的知识和学习新类。

从开集识别问题中得到灵感，其中测试场景不一定属于训练分布。

GDnumb：（1）贪婪地将样本存储在内存中；（2）在测试时，只使用内存中的样本从头开始训练模型，给定一个内存预算，采样器贪婪地存储来自数据流的样本，同时确保类是平衡的，并且，在推理时，学习者（神经网络）使用存储在内存中的所有样本从头开始训练（因此是愚蠢的）。这是一种简单的方法，如上面所讨论的，它不会对标签空间的增长性质、任务边界、在线与离线以及数据流提供它们的样本的排序施加任何限制

1、介绍：

GDnumb这个算法不是专门设置在CL的问题上，但是目前有许多不同的算法都有简单的限制以至于他们甚至打破了持续学习的概念，例如：约束条件是可能会采取一个给定的先验标签子集。

我们首先提供了一个用于分类的CL的一般公式。然后，我们研究了现有CL算法的流行变体，并根据它们对上述一般公式所施加的简化假设对其进行分类。讨论它们如何对标签空间不断增长的性质、标签空间的大小或可用资源施加约束

基本上没有一个场景实际上模拟了暴露在现实世界上面临CL的一般形式。

GDnumb：提出了与流行和广泛使用的假设、评估指标相关的关注，也质疑了最近提出的各种持续学习算法的有效性。

2、问题的公式化、假设、趋势

（当一个学习的机器在学习到到某些不认识的任务时候，将学习一些未知的对象通过要求数据库提供标签，同时，将更新其已知对象的信息如果他们的新实例提供了额外的线索有用的任务。）

一个分类持续学习的现实公式是，有一个学习者可访问的训练样本或数据流，每个样本包含一个双元组(xt，yt)，其中t代表时间戳或样本索引。

让Yt=∪ti=1yi是直到时间t之前看到的标签集，Yt−1⊆Yt 意味着流可能会给我们一个属于新类或属于旧类的样本

（废话，新进来的标签包含旧的，肯定会这样）

表示该样本不属于任何一个学习类。（预测出来的标签，在预测的时候，假设的是对这个世界的信息并不完整，测试集可能跟训练集不属于同一个分布，可以通过学习推断为y¯的样本的语义来提高其对世界的知识）

2.1在CL中的简单假设

如果在计算和存储中不加以限制可能会有一个不错的函数映射关系，达到比较好的准确率，但是缺乏关于现实的信息和输出的空间的估计，这个问题就变得比较难了，这会导致我们往往需要加一些额外的简化约束和假设。

一个共同的假设是，测试样本总是属于训练分布。

不相交的方式：这个公式被用于几乎所有最近的工作，假设是在一个特定的时间，数据流将提供样本特定的任务，在一个预定义的任务，目的是学习主要的映射通过每个任务时间的顺序。

关于样本任务间的边界：如标签控件被划分为不想交的子集（可以是随机的，也可以是知情的分割），其中每个标签子集Yi代表一个任务，这些集合之间的急剧转换称为任务边界。

任务增量v/s类增量：CL公式的一个流行选择是任务增量持续学习(TI-CL)，与不相交任务假设一起，任务信息(或id)在训练和推理过程中也由数据库传递。

TI-CL:一个三元组(x，y，α)，其中α∈N表示任务标识符。这个公式也被称为多头,如果输入为(x，α=3)，这意味着样本要么属于类4，要么属于类5.

然而，在一个类增量公式(CI-CL)中，也被称为单头，我们没有关于任务id的任何这样的信息。

在线持续学习VS离线持续学习：界限任务只限制了标签控制和限制其大小，并没有对模型对限制，学习范式可以根据空间预算存储来自流的特定于任务的样本，然后使用它们来更新参数。

在线：即使学习者可以在样本出现时存储样本，也不允许多次使用样本进行参数更新。

离线：允许不受限制地访问与特定任务对应的整个数据集（而不是访问之前的数据集），并且可以在执行多次传递数据时，通过反复访问样本来使用这个数据集来学习参数更新

基于内存的CL：由于缺少之前任务中的样本，由于灾难性遗忘，很难学习将样本与当前和以前的任务区分开来。

在TI-CL中，通常很少观察到遗忘，因为给定的任务标识符作为任务边界的指标，因此模型不需要学习区分任务之间的标签，

因为这玩意难，所以我们搞了个内存空间来存储之前的样本。

2.2最近的趋势在持续学习：

处理遗忘的方法进行分类的，如基于（1）正则化、基于（2）重放（或记忆）、基于（3）蒸馏和基于（4）参数隔离

转向TI-CLv/sCI-CL，这是两种极端的情况，其中CI-CL（单头）面临缩放问题，因为对|limt→∞Yt|的大小没有限制，而TI-CL（多头）在具有|标签的类之间施加了一个固定的、连贯的两级层次结构。当源源不断的任务进入的时候，则CICL这个情况最终网络头会不断变大。

如果没有适当的度量标准或程序来量化各种CL算法如何平衡空间和时间的复杂性，将它们分为离线和在线可能会导致错误的结论。

3、GDumb：

Sampler：渐近平衡类分布，它是贪婪的，因为每当它遇到一个新类时，采样器只是为该类创建一个容器，并开始从旧的样本中删除样本，特别是从样本数量最多的样本中（无论类的样本多少，我们都必须要以同等的重要性对待）

模型学习了对时间t之前看到的所有标签进行分类，在推理的时候的模型如下：

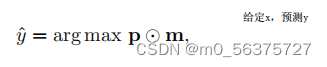
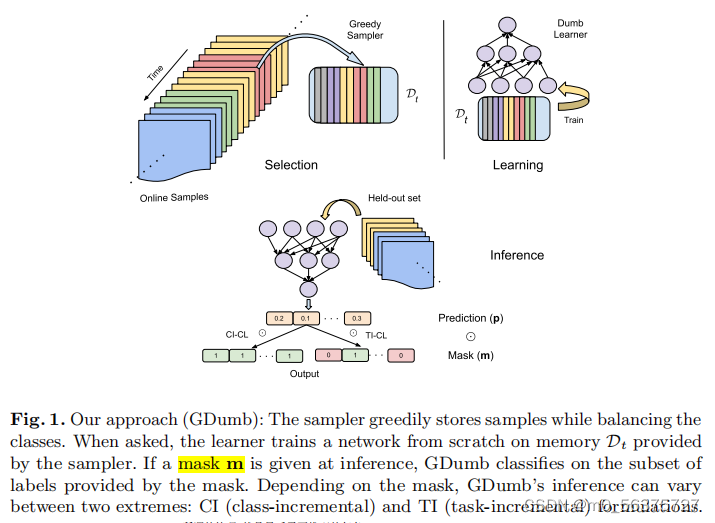
当被问及时，学习者根据采样器提供的内存Dt从头训练网络。如果在推理时给出一个掩码m，GDumb将对掩码提供的标签子集进行分类。根据掩码的不同，GDumb的推理可以在两个极端之间有所不同：CI（类增量）公式和TI（任务增量）公式。

（最终分类器优化）关于哈达曼乘积Hadamard product：把所有预测出来的结果进行一个哈达曼乘积，我们给定一个mask M，M属于（0,1），M可以屏蔽任何的子集，如果乘积矩阵是由1来组成的，那么就符合我们的类增量的情况，因为我们所有的类都能正常表示出来，当我们的M屏蔽了它特定的子集，那么就符合了所设定的多头输出，也就是任务增量。

4、实验

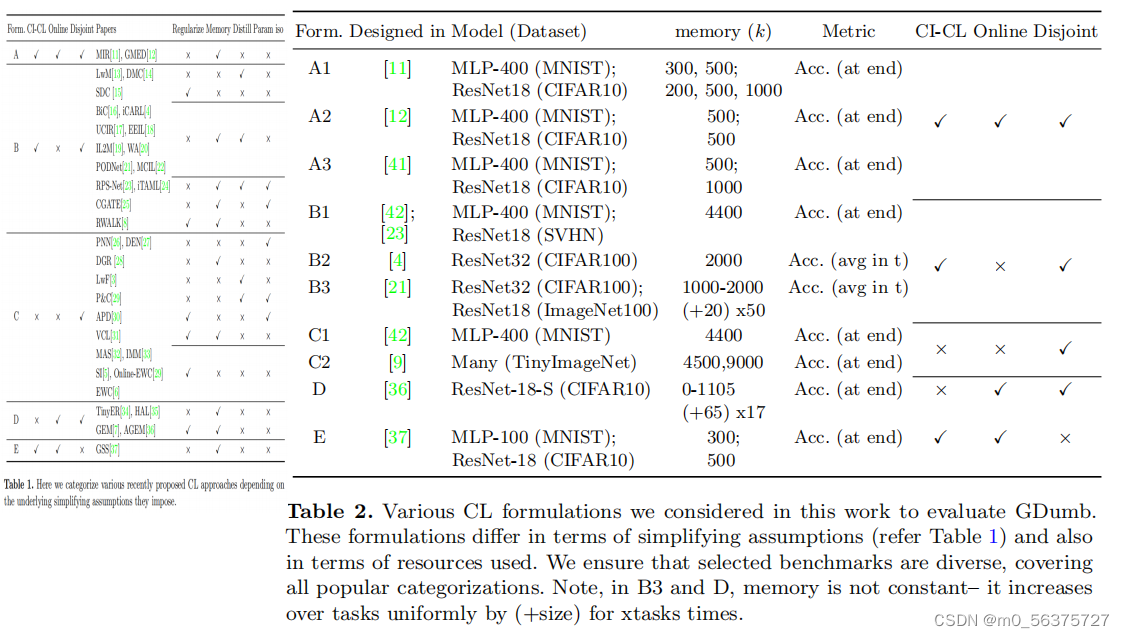
在表一中，共有5种公式，在本工作中考虑的各种CL公式来评估GDumb。这些公式在简化假设方面（见表1）和所使用的资源方面也有所不同。我们确保所选的基准测试是多样化的，涵盖了所有流行的分类。

实验细节：GDumb使用了一个SGD优化器，固定的批量大小为16，学习率[0.05,0.0005]，一个SGDR[45]时间表与T0=1，Tmult=2和1epoch的温暖开始。早期停止，耐心等待1个周期的SGDR，并使用标准的数据增强。GDumb使用cutmix和p=0.5和α=1.0对除MNIST之外的所有数据集进行正则化。

结果：

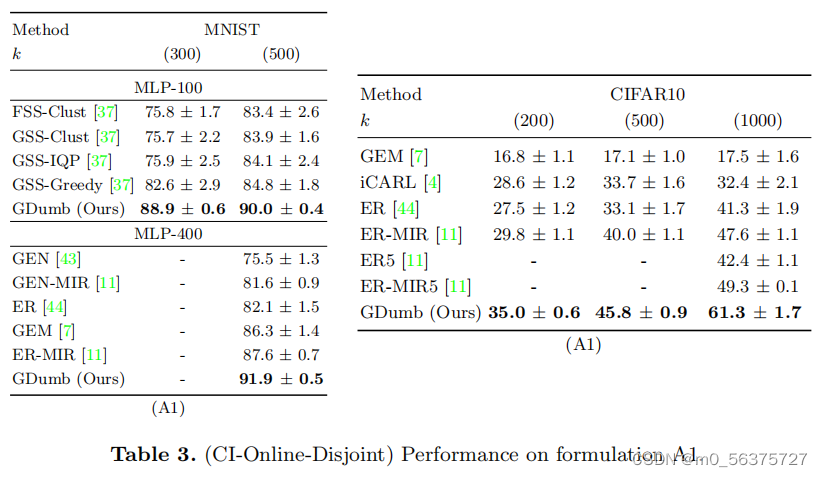
未来趋势：

主动抽样：给定一个重要值vt∈R+（主动学习者）以及样本(xtyt)，我们可以扩展我们的采样器的目标存储最重要的样本(最大化P|Dc|i=1vi)对于任何给定的类c存储大小k。这将允许一个算法拒绝不那么重要的样本。当然，目前还不清楚如何学会量化一个样本的重要性。

动态概率掩蔽：类似地，我们可以将GDumb超越确定性(mi∈{0,1})扩展到概率性(mi∈[0,1])，也就是说我们在推理的时候增加上一个动态的概率可以得到每一个类的关系。

总结：这篇文章只是提供了一种从头学习的方法，给我们提供了一种不错的采样思路，与16年的icarl有异曲同工之妙，Gdumb这种简单的学习方法在最近的综述中斩获了不错的反响，特别在于中类型的数据集和类增量的设定上。

PS：水平有限，有错望指出！谢谢

最后

以上就是贪玩汉堡为你收集整理的GDumb: A Simple Approach that Questions OurProgress in Continual Learning（论文总结）摘要：1、介绍：2、问题的公式化、假设、趋势3、GDumb：4、实验结果：未来趋势：的全部内容，希望文章能够帮你解决GDumb: A Simple Approach that Questions OurProgress in Continual Learning（论文总结）摘要：1、介绍：2、问题的公式化、假设、趋势3、GDumb：4、实验结果：未来趋势：所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。