人脸姿态估计简单预研

一、 背景介绍

其实背景很简单，就是有些算法针对正脸的效果很好，但是对于特别大的侧脸，效果就不是很好，所以需要需要根据人脸姿态来进行过滤。

二、 算法的简要介绍

1. 什么是姿态估计

在计算机视觉中，对象的姿态是指其相对于相机的相对方向和位置，我们可以通过相对于相机移动对象，也可以相对于对象移动相机，还可以同时移动相机和对象，如果相机和对象保持相对静止，虽然相机和对象在世界坐标系中的位置改变了，但是两种之间的关系并没有变化，换句话说你从相机中获得对象的图片并没有变化，那么我们也可以认为姿态没有变化

在计算机视觉术语中，姿态估计的问题也被称为PnP问题（Perspective-n-Point problem），wiki对这个问题的定义如下：

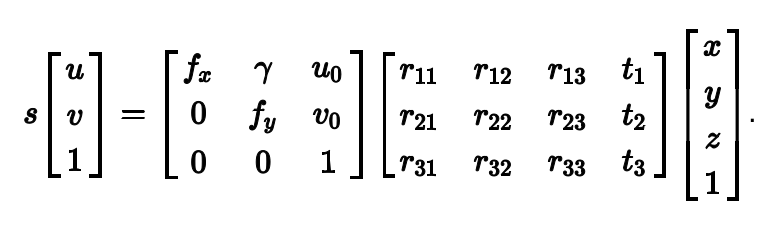
2. 如何用数学的方式来表示相机运动呢？

3D刚性对象相对于相机只有两种运动。

• 平移：将摄像机从其当前3D位置（X，Y，Z）移动到新的3D位置（X’，Y’，Z’）称为平移。 平移具有3个自由，可以在X，Y或Z方向上移动。 平移由向量$\mathbf{t}$表示，该向量等于（X’-X，Y’-Y，Z’-Z）。

• 旋转：您也可以绕X，Y和Z轴旋转相机。 因此，旋转也具有三个自由度。 有多种表示旋转的方法。 您可以使用欧拉角（滚动角，俯仰角和偏航角），3×3旋转矩阵或旋转方向（即轴）和角度来表示它。

3. 姿态估计需要什么呢？

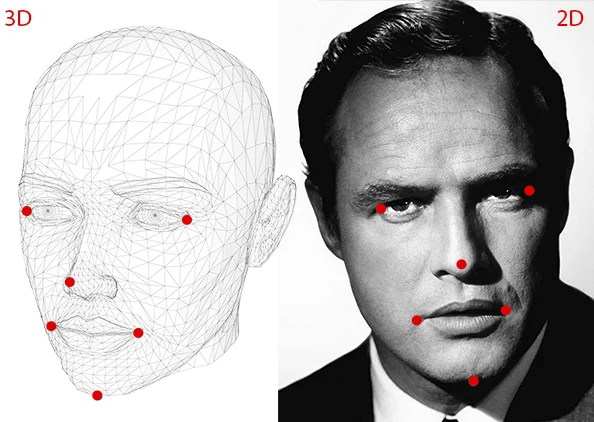
a. 由上图我们可以看出需要一些2D（x，y）的坐标点，对应到人脸姿态估计，其实就是需要人脸关键点坐标，
b. 实际情况下我们还需要获得人脸在三维空间中的坐标，这个实际情况下，我们可以使用平均脸模型坐标就可以了

看来很多教程，一般使用的都是上图中的6个关键点坐标：
鼻尖：（0.0，0.0，0.0）
下巴：（0.0，-330.0，-65.0）
左眼的左上角：（-225.0f，170.0f，-135.0）
右眼的右上角：（225.0，170.0，-135.0）
嘴左角：（-150.0，-150.0，-125.0）
嘴右角：（150.0，-150.0，-125.0）

c. 相机的内参，在我们实际应用相机的时候，都需要对相机进行标定，得到对应相机的焦距，光心和畸变参数，但是博客中也给出了近似的方法来计算相机内参

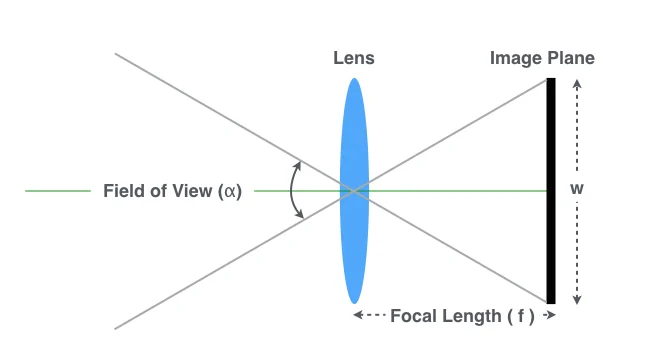
根据三角形的一些知识可以得到
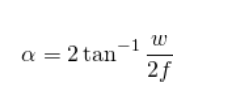那么上式可以改写为：
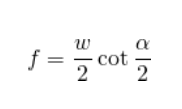根据上面的公式，根据以上公式，如果您知道图像宽度w和视场$\alpha$，则可以计算以像素为单位的焦距f。

还有一些更加复杂的近似方法，我们到这里基本可以解释代码原理了，如果要看详细的算法请参考2.

4. 怎么进行姿态估计呢？

有几种用于姿态估计的算法。 第一个已知的算法可以追溯到1841年。解释这些算法的细节超出了本文的讨论范围，但这是一个基本概念。

这里有三个坐标系在起作用。 上面显示的各种面部特征的3D坐标位于世界坐标中。 如果我们知道旋转和平移（即位姿），则可以将世界坐标中的3D点转换为相机坐标中的3D点。 可以使用相机的固有参数（焦距，光学中心等）将相机坐标中的3D点投影到图像平面（即图像坐标系）上。
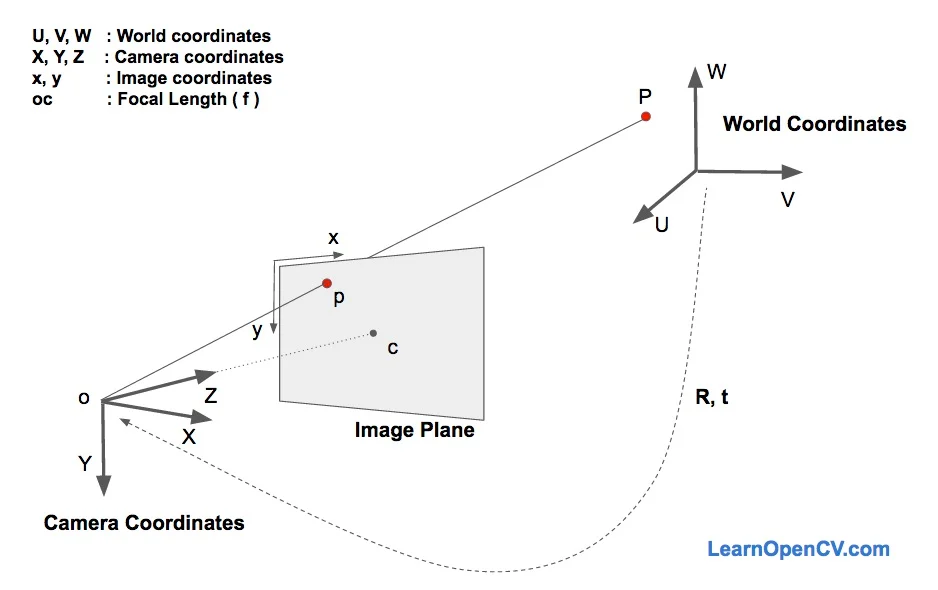其实还是很好理解的，在上图中，o是相机的中心，图中所示的平面是图像平面。我们感兴趣的是找出哪些方程控制着3D点P在图像平面上的投影p。
假设我们知道3D点P在世界坐标中的位置（U，V，W）。如果我们知道世界坐标相对于相机坐标的旋转 mathbf {R}（3×3矩阵）和平移$\mathbf{t}$（3×1向量），则可以计算位置（X相机坐标系中的点P，请使用以下公式。

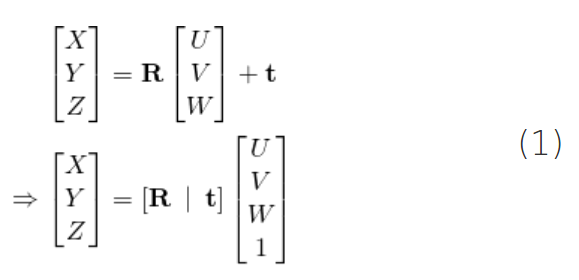
展开上面的式子，可以得到：

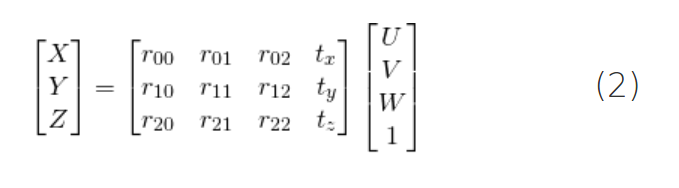
如果曾经学习过线性代数课程，就可以认识到，如果我们知道足够数量的点对应关系（即（X，Y，Z）和（U，V，W）），则上面是一个线性方程组，其中$r_{ij}$和$(t_x，t_y，t_z)$是未知数，可以轻松地求解未知数。

a. Direct Linear Transform

We do know many points on the 3D model ( i.e. (U, V, W) ), but we do not know (X, Y, Z). We only know the location of the 2D points ( i.e. (x, y) ). In the absence of radial distortion, the coordinates (x, y) of point p in the image coordinates is given by

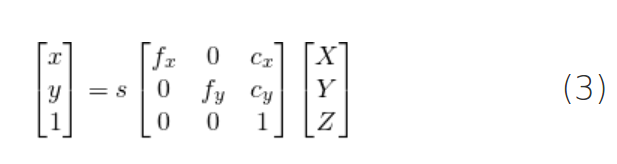
where, $f_x$ and $f_y$ are the focal lengths in the x and y directions, and $(c_x,c_y)$ is the optical center. Things get slightly more complicated when radial distortion is involved and for the purpose of simplicity I am leaving it out.

What about that s in the equation ? It is an unknown scale factor. It exists in the equation due to the fact that in any image we do not know the depth. If you join any point P in 3D to the center o of the camera, the point p, where the ray intersects the image plane is the image of P. Note that all the points along the ray joining the center of the camera and point P produce the same image. In other words, using the above equation, you can only obtain (X, Y, Z) up to a scale s.

Now this messes up equation 2 because it is no longer the nice linear equation we know how to solve. Our equation looks more like

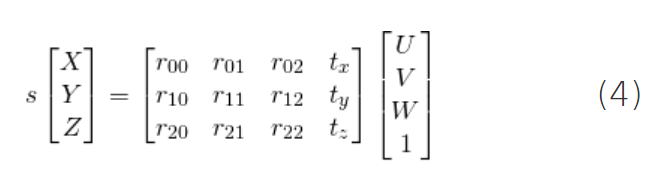
Fortunately, the equation of the above form can be solved using some algebraic wizardry using a method called Direct Linear Transform (DLT). You can use DLT any time you find a problem where the equation is almost linear but is off by an unknown scale.

b. Levenberg-Marquardt Optimization

The DLT solution mentioned above is not very accurate because of the following reasons . First, rotation $\mathbf{R}$ has three degrees of freedom but the matrix representation used in the DLT solution has 9 numbers. There is nothing in the DLT solution that forces the estimated 3×3 matrix to be a rotation matrix. More importantly, the DLT solution does not minimize the correct objective function. Ideally, we want to minimize the reprojection error that is described below.

As shown in the equations 2 and 3, if we knew the right pose ( $\mathbf{R}$ and $\mathbf{t}$ ), we could predict the 2D locations of the 3D facial points on the image by projecting the 3D points onto the 2D image. In other words, if we knew $\mathbf{R}$ and $\mathbf{t}$ we could find the point p in the image for every 3D point P.

We also know the 2D facial feature points ( using Dlib or manual clicks ). We can look at the distance between projected 3D points and 2D facial features. When the estimated pose is perfect, the 3D points projected onto the image plane will line up almost perfectly with the 2D facial features. When the pose estimate is incorrect, we can calculate a re-projection error measure — the sum of squared distances between the projected 3D points and 2D facial feature points.

As mentioned earlier, an approximate estimate of the pose ( $\mathbf{R}$ and $\mathbf{t}$ ) can be found using the DLT solution. A naive way to improve the DLT solution would be to randomly change the pose ( $\mathbf{R}$ and $\mathbf{t}$ ) slightly and check if the reprojection error decreases. If it does, we can accept the new estimate of the pose. We can keep perturbing $\mathbf{R}$ and $\mathbf{t}$ again and again to find better estimates. While this procedure will work, it will be very slow. Turns out there are principled ways to iteratively change the values of $\mathbf{R}$ and $\mathbf{t}$ so that the reprojection error decreases. One such method is called Levenberg-Marquardt optimization. Check out more details on Wikipedia.

c. OpenCV solvePnP

In OpenCV the function solvePnP and solvePnPRansac can be used to estimate pose.

solvePnP implements several algorithms for pose estimation which can be selected using the parameter flag. By default it uses the flag SOLVEPNP_ITERATIVE which is essentially the DLT solution followed by Levenberg-Marquardt optimization. SOLVEPNP_P3P uses only 3 points for calculating the pose and it should be used only when using solvePnPRansac.

In OpenCV 3, two new methods have been introduced — SOLVEPNP_DLS and SOLVEPNP_UPNP. The interesting thing about SOLVEPNP_UPNP is that it tries to estimate camera internal parameters also.

C++: bool solvePnP(InputArray objectPoints, InputArray imagePoints, InputArray cameraMatrix, InputArray distCoeffs, OutputArray rvec, OutputArray tvec, bool useExtrinsicGuess=false, int flags=SOLVEPNP_ITERATIVE )

Python: cv2.solvePnP(objectPoints, imagePoints, cameraMatrix, distCoeffs[, rvec[, tvec[, useExtrinsicGuess[, flags]]]]) → retval, rvec, tvec

Parameters:

objectPoints – Array of object points in the world coordinate space. I usually pass vector of N 3D points. You can also pass Mat of size Nx3 ( or 3xN ) single channel matrix, or Nx1 ( or 1xN ) 3 channel matrix. I would highly recommend using a vector instead.

imagePoints – Array of corresponding image points. You should pass a vector of N 2D points. But you may also pass 2xN ( or Nx2 ) 1-channel or 1xN ( or Nx1 ) 2-channel Mat, where N is the number of points.

cameraMatrix – Input camera matrix A = begin{bmatrix} f_x & 0 & c_x \ 0 & f_y & c_y \ 0 & 0 & 1 end{bmatrix}. Note that f_x, f_y can be approximated by the image width in pixels under certain circumstances, and the c_x and c_y can be the coordinates of the image center.

distCoeffs – Input vector of distortion coefficients (k_1, k_2, p_1, p_2[, k_3[, k_4, k_5, k_6],[s_1, s_2, s_3, s_4]]) of 4, 5, 8 or 12 elements. If the vector is NULL/empty, the zero distortion coefficients are assumed. Unless you are working with a Go-Pro like camera where the distortion is huge, we can simply set this to NULL. If you are working with a lens with high distortion, I recommend doing a full camera calibration.

rvec – Output rotation vector.

tvec – Output translation vector.

useExtrinsicGuess – Parameter used for SOLVEPNP_ITERATIVE. If true (1), the function uses the provided rvec and tvec values as initial approximations of the rotation and translation vectors, respectively, and further optimizes them.

flags –
Method for solving a PnP problem:

SOLVEPNP_ITERATIVE Iterative method is based on Levenberg-Marquardt optimization. In this case, the function finds such a pose that minimizes reprojection error, that is the sum of squared distances between the observed projections imagePoints and the projected (using projectPoints() ) objectPoints .

SOLVEPNP_P3P Method is based on the paper of X.S. Gao, X.-R. Hou, J. Tang, H.-F. Chang “Complete Solution Classification for the Perspective-Three-Point Problem”. In this case, the function requires exactly four object and image points.

SOLVEPNP_EPNP Method has been introduced by F.Moreno-Noguer, V.Lepetit and P.Fua in the paper “EPnP: Efficient Perspective-n-Point Camera Pose Estimation”.

The flags below are only available for OpenCV 3

SOLVEPNP_DLS Method is based on the paper of Joel A. Hesch and Stergios I. Roumeliotis. “A Direct Least-Squares (DLS) Method for PnP”.

SOLVEPNP_UPNP Method is based on the paper of A.Penate-Sanchez, J.Andrade-Cetto, F.Moreno-Noguer. “Exhaustive Linearization for Robust Camera Pose and Focal Length Estimation”. In this case the function also estimates the parameters f_x and f_y assuming that both have the same value. Then the cameraMatrix is updated with the estimated focal length.

d. OpenCV solvePnPRansac

solvePnPRansac is very similar to solvePnP except that it uses Random Sample Consensus ( RANSAC ) for robustly estimating the pose.

Using RANSAC is useful when you suspect that a few data points are extremely noisy. For example, consider the problem of fitting a line to 2D points. This problem can be solved using linear least squares where the distance of all points from the fitted line is minimized. Now consider one bad data point that is wildly off. This one data point can dominate the least squares solution and our estimate of the line would be very wrong. In RANSAC, the parameters are estimated by randomly selecting the minimum number of points required. In a line fitting problem, we randomly select two points from all data and find the line passing through them. Other data points that are close enough to the line are called inliers. Several estimates of the line are obtained by randomly selecting two points, and the line with the maximum number of inliers is chosen as the correct estimate.

The usage of solvePnPRansac is shown below and parameters specific to solvePnPRansac are explained.

 C++: void solvePnPRansac(InputArray objectPoints, InputArray imagePoints, InputArray cameraMatrix, InputArray distCoeffs, OutputArray rvec, OutputArray tvec, bool useExtrinsicGuess=false, int iterationsCount=100, float reprojectionError=8.0, int minInliersCount=100, OutputArray inliers=noArray(), int flags=ITERATIVE )

Python: cv2.solvePnPRansac(objectPoints, imagePoints, cameraMatrix, distCoeffs[, rvec[, tvec[, useExtrinsicGuess[, iterationsCount[, reprojectionError[, minInliersCount[, inliers[, flags]]]]]]]]) → rvec, tvec, inliers

iterationsCount – The number of times the minimum number of points are picked and the parameters estimated.
reprojectionError – As mentioned earlier in RANSAC the points for which the predictions are close enough are called “inliers”. This parameter value is the maximum allowed distance between the observed and computed point projections to consider it an inlier.
minInliersCount – Number of inliers. If the algorithm at some stage finds more inliers than minInliersCount , it finishes.
inliers – Output vector that contains indices of inliers in objectPoints and imagePoints .

3. Python代码实例

import dlib
import cv2
import numpy as np
import math


# Checks if a matrix is a valid rotation matrix.
def isRotationMatrix(R):
    Rt = np.transpose(R)
    shouldBeIdentity = np.dot(Rt, R)
    I = np.identity(3, dtype=R.dtype)
    n = np.linalg.norm(I - shouldBeIdentity)
    return n < 1e-6


# Calculates rotation matrix to euler angles
# The result is the same as MATLAB except the order
# of the euler angles ( x and z are swapped ).
def rotationMatrixToEulerAngles(R):
    assert (isRotationMatrix(R))

    sy = math.sqrt(R[0, 0] * R[0, 0] + R[1, 0] * R[1, 0])

    singular = sy < 1e-6

    if not singular:
        x = math.atan2(R[2, 1], R[2, 2])
        y = math.atan2(-R[2, 0], sy)
        z = math.atan2(R[1, 0], R[0, 0])
    else:
        x = math.atan2(-R[1, 2], R[1, 1])
        y = math.atan2(-R[2, 0], sy)
        z = 0

    return np.array([x, y, z])


class Eestimation():
    def __init__(self):
        self.predictor_path = './shape_predictor_68_face_landmarks.dat'
        self.detector = dlib.get_frontal_face_detector()
        self.predictor = dlib.shape_predictor(self.predictor_path)

    def faceDetAli(self, img):
        img_gray = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)
        rects = self.detector(img_gray, 0)

        landmarks = []

        for i in range(len(rects)):
            landmarks_node = np.array([[p.x, p.y] for p in self.predictor(img_gray, rects[i]).parts()])
            for idx, point in enumerate(landmarks_node):
                pos = tuple(point)
                cv2.circle(img, pos, 2, color=(0, 255, 0))

            landmarks.append(landmarks_node)
        cv2.imwrite("./test_landmark.jpg", img)
        return landmarks

    def Estimation(self, landmarks, img):

        size = img.shape
        # estimate internals
        '''method one: estimate the camera matrix'''
        # focal_length = size[1]
        # center = (size[1] / 2, size[0] / 2)
        # camera_matrix = np.array(
        #     [[focal_length, 0, center[0]],
        #      [0, focal_length, center[1]],
        #      [0, 0, 1]], dtype="double"
        # )
        '''method two: estimate the camera matrix'''
        cx = size[1] / 2
        cy = size[2] / 2
        fx = cx / np.tan(60 / 2 * np.pi / 180)
        fy = fx
        camera_matrix = np.float32([[fx, 0.0, cx],
                                    [0.0, fy, cy],
                                    [0.0, 0.0, 1.0]])

        dist_coeffs = np.zeros((4, 1))  # Assuming no lens distortion

        # 3D model points.
        model_points = np.array([
            (0.0, 0.0, 0.0),  # Nose tip
            (0.0, -330.0, -65.0),  # Chin
            (-225.0, 170.0, -135.0),  # Left eye left corner
            (225.0, 170.0, -135.0),  # Right eye right corne
            (-150.0, -150.0, -125.0),  # Left Mouth corner
            (150.0, -150.0, -125.0)  # Right mouth corner

        ])

        for i in range(len(landmarks)):
            print(landmarks[i].shape)
            nose_tip = landmarks[i][30, :]
            chin = landmarks[i][8, :]
            lelc = landmarks[i][36, :]
            rerc = landmarks[i][45, :]
            lmc = landmarks[i][48, :]
            rmc = landmarks[i][54, :]
            image_points = np.array([
                nose_tip,  # Nose tip
                chin,  # Chin
                lelc,  # Left eye left corner
                rerc,  # Right eye right corne
                lmc,  # Left Mouth corner
                rmc  # Right mouth corner
            ], dtype="double")
            print(image_points.shape)
            (success, rotation_vector, translation_vector) = cv2.solvePnP(model_points, image_points, camera_matrix,
                                                                          dist_coeffs, flags=cv2.SOLVEPNP_ITERATIVE)

            print(rotation_vector)
            (R, j) = cv2.Rodrigues(rotation_vector)
            print(R)
            print(rotationMatrixToEulerAngles(R))
            # Project a 3D point (0, 0, 1000.0) onto the image plane.
            # We use this to draw a line sticking out of the nose

            (nose_end_point2D, jacobian) = cv2.projectPoints(np.array([(0.0, 0.0, 1000.0)]), rotation_vector,
                                                             translation_vector, camera_matrix, dist_coeffs)

            for p in image_points:
                cv2.circle(img, (int(p[0]), int(p[1])), 3, (0, 0, 255), -1)

            p1 = (int(image_points[0][0]), int(image_points[0][1]))
            p2 = (int(nose_end_point2D[0][0][0]), int(nose_end_point2D[0][0][1]))

            cv2.line(img, p1, p2, (255, 0, 0), 2)
            cv2.imwrite("./pose_res_two.jpg", img)
            return img

    def total_img(self):
        img_path = './pose.jpg'
        img = cv2.imread(img_path)
        landmarks = self.faceDetAli(img)
        img_new = self.Estimation(landmarks, img)

    def total_video(self):
        video = cv2.VideoCapture(
            "./2_out.mp4")
        print("the fps of the video: ", video.get(5))
        fourcc = cv2.VideoWriter_fourcc(*'XVID')
        out = cv2.VideoWriter("./pose_res.avi", fourcc, 60.0, (1920, 1080))
        flag = True
        while (flag):
            ret, recv_frame = video.read()

            if ret:
                landmarks = self.faceDetAli(recv_frame)
                img_new = self.Estimation(landmarks, recv_frame)

                out.write(img_new)
            else:
                flag = False

        video.release()
        out.release()


if __name__ == '__main__':
    est = Eestimation()
    # est.total_video()
    est.total_img()

附上结果图，其实这种人脸姿态估计是依赖于特征点的，如果关键点定位不准确，那么姿态估计也会出现问题，但是如果使用end-to-end又要考虑时间开销和硬件开销，这是一个简单的算法预研，后期怎么做还得考虑一下

主要参考地址为：

1. https://www.learnopencv.com/head-pose-estimation-using-opencv-and-dlib/
2. https://www.learnopencv.com/approximate-focal-length-for-webcams-and-cell-phone-cameras/

最后

以上就是高高网络为你收集整理的人脸姿态估计简单预研（DLIB+OpenCV，含python代码示例）人脸姿态估计简单预研的全部内容，希望文章能够帮你解决人脸姿态估计简单预研（DLIB+OpenCV，含python代码示例）人脸姿态估计简单预研所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。