传递函数矩阵形式转化成状态空间形式(含实现程序)1.一般形式2.零极点增益形式

78 阅读 0 评论 52 点赞

我是靠谱客的博主暴躁小懒虫，这篇文章主要介绍传递函数矩阵形式转化成状态空间形式(含实现程序)1.一般形式2.零极点增益形式，现在分享给大家，希望可以做个参考。

最近看文献总看到离散形式和传递函数矩阵等类似的问题，特在此记录一下，本篇先讲解传递函数矩阵转化成状态空间的几种实现方法，后续会记录以下离散系统的仿真。

下面分两种情形，一种是一般的形式，一种是零极点增益形式，且均以连续为例，因为离散也是一样的，只不过加上采样时间即可。

1.一般形式

以一个简单的传递函数矩阵为例：

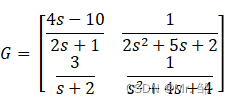
话不多说，直接给出MATLAB的实现程序，这里展示三种方法：

方法一：

思路是逐个转化后进行合并。

% from u1 to y1
num1=[4 -10];
den1=[2 1];
[A11,B11,C11,D11]=tf2ss(num1,den1);
S11=ss(A11,B11,C11,D11);
% from u2 to y1
num2=[3];
den2=[1 2];
[A12,B12,C12,D12]=tf2ss(num2,den2);
S12=ss(A12,B12,C12,D12);
% from u1 to y2
num3=[1];
den3=[2 5 2];
[A21,B21,C21,D21]=tf2ss(num3,den3);
S21=ss(A21,B21,C21,D21);
% from u2 to y2
num4=[1];
den4=[1 4 4];
[A22,B22,C22,D22]=tf2ss(num4,den4);
S22=ss(A22,B22,C22,D22);

sys=[S11 S12;S21 S22]

输出结果：

sys =

A =
x1 x2 x3 x4 x5 x6
x1 -0.5 0 0 0 0 0
x2 0 -2 0 0 0 0
x3 0 0 -2.5 -1 0 0
x4 0 0 1 0 0 0
x5 0 0 0 0 -4 -4
x6 0 0 0 0 1 0

B =
u1 u2
x1 1 0
x2 0 1
x3 1 0
x4 0 0
x5 0 1
x6 0 0

C =
x1 x2 x3 x4 x5 x6
y1 -6 3 0 0 0 0
y2 0 0 0 0.5 0 1

D =
u1 u2
y1 2 0
y2 0 0

方法二：

num={[4 -10],[3];[1],[1]};
den={[2 1],[1 2];[2 5 2],[1 4 4]};
G=tf(num,den);
sys = ss(G)

输出结果：

sys =

A =
x1 x2 x3 x4 x5 x6
x1 -0.5 0 0 0 0 0
x2 0 -2.5 -1 0 0 0
x3 0 1 0 0 0 0
x4 0 0 0 -2 0 0
x5 0 0 0 0 -4 -2
x6 0 0 0 0 2 0

B =
u1 u2
x1 2 0
x2 0.5 0
x3 0 0
x4 0 2
x5 0 0.5
x6 0 0

C =
x1 x2 x3 x4 x5 x6
y1 -3 0 0 1.5 0 0
y2 0 0 1 0 0 1

D =
u1 u2
y1 2 0
y2 0 0
方法三：

H = [tf([4 -10],[2 1]),tf([3],[1 2]);tf([1],[2 5 2]),tf([1],[1 4 4])];
sys = ss(H)

输出结果：

注：可以看到方法二和方法三比较简洁，结果也是一致的。至于方法一个人认为是由于转化的形式不唯一，其实系统是一样的。

2.零极点增益形式

这里以一个含复数的例子为参考：

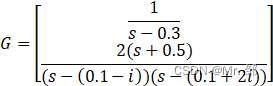
Z = {[] ; -0.5};
P = {0.3 ; [0.1-1i 0.1+2i]};
K = [1 ; 2];
G = zpk(Z,P,K)
sys = ss(G)

输出结果：

G =

From input to output...
1
1: -------
(s-0.3)

2 (s+0.5)
2: -------------------------
(s-(0.1-1i)) (s-(0.1+2i))

Continuous-time zero/pole/gain model.

sys =

A =
x1 x2 x3
x1 0.3 0 0
x2 0 0.1-1i 1.08
x3 0 0 0.1+2i

B =
u1
x1 1
x2 0
x3 2

C =
x1 x2 x3
y1 1 0 0
y2 0 0.556-0.926i 1

D =
u1
y1 0
y2 0

Continuous-time state-space model.