信号与系统的仿真习题五

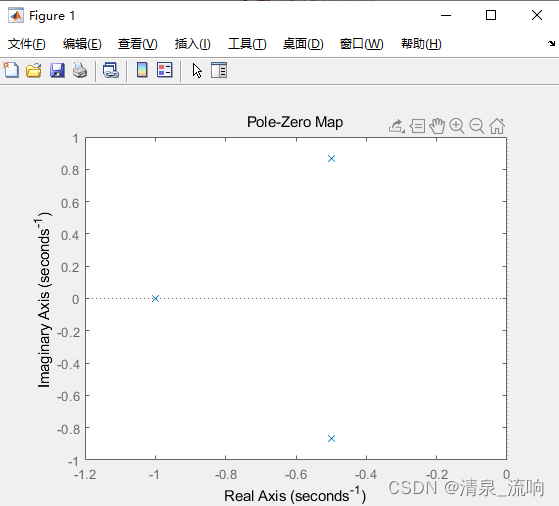
一、已知系统函数为H（s）=1/（s^3+2s^2+2s+1）,试画出其零极点分布图
求解系统的冲激响应h（t）和频率响应H（jw），并判断系统是否稳定
结论：系统函数的极点位于s左半平面，因此系统是稳定的

代码如下：

clc;
clear;
close all;
num=[1];
den=[1 2 2 1];
sys=tf(num,den);%num和den分别为系统函数H（s）的分子多项式和分母多项式的系数向量
poles=roots(den);
figure;
pzmap(sys);%表示画出sys所描述系统的零极点图
t=0:0.02:10;
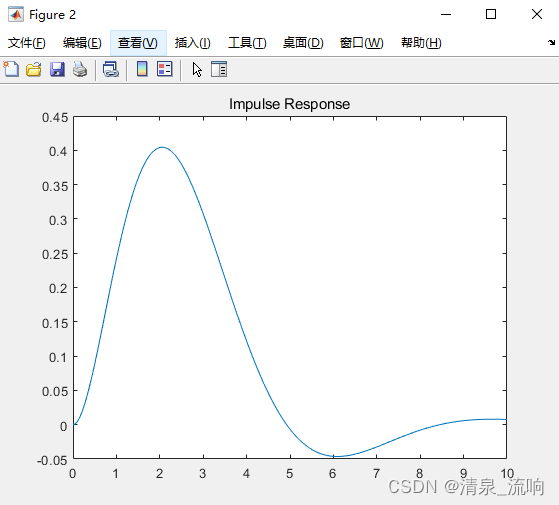
h=impulse(num,den,t);%求系统的冲激响应h（t）
figure;
plot(t,h);
title('Impulse Response');
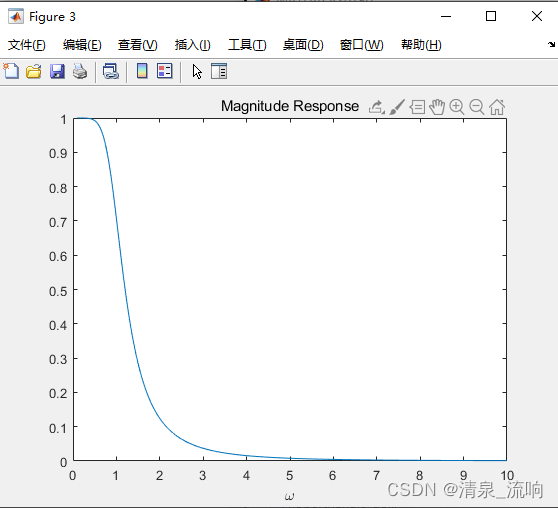
[H,w]=freqs(num,den);%求系统的频率响应H（jw）
figure;
plot(w,abs(H));
xlabel('omega');
title('Magnitude Response');

运行结果如下：

 二、已知一离散因果LTI系统的系统函数为：H(z)=(z^2+2z+1)/(z^3-0.5z^2-0.005z^-1 +0.3)
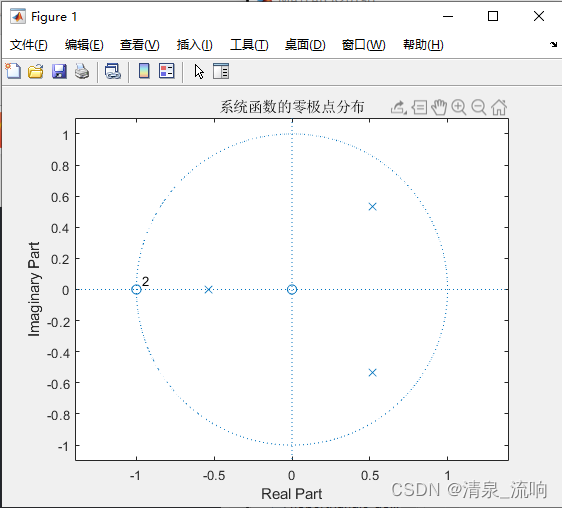
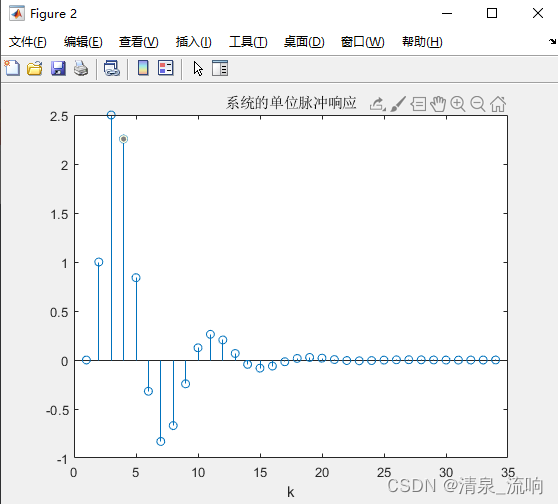
试画出系统的零极点分布图，求系统的单位脉冲响应h[k]和频率响应H(e^jΩ),并判断系统是否稳定
根据已知的H（z），可以用zplane函数画出系统的零极点分布图。
利用impz函数和freqz函数求系统的单位脉冲响应和频率响应时，需要将H（z）改写成
H(z)=(z^-1 +2z^-2 +z^-3)/(1-0.5z^-1 -0.005z^-2 +0.3z^-3)
结论：符号o旁边的数字表示零点的阶数，虚线是单位圆，由图可知，该因果系统的极点全部在单位圆内，因此系统是稳定的
代码如下：

b=[1 2 1];
a=[1 -0.5 -0.005 0.3];
figure;
zplane(b,a);
title('系统函数的零极点分布');
num=[0 1 2 1];
den=[1 -0.5 -0.005 0.3];
h=impz(num,den);
figure;
stem(h);
xlabel('k');
title('系统的单位脉冲响应');
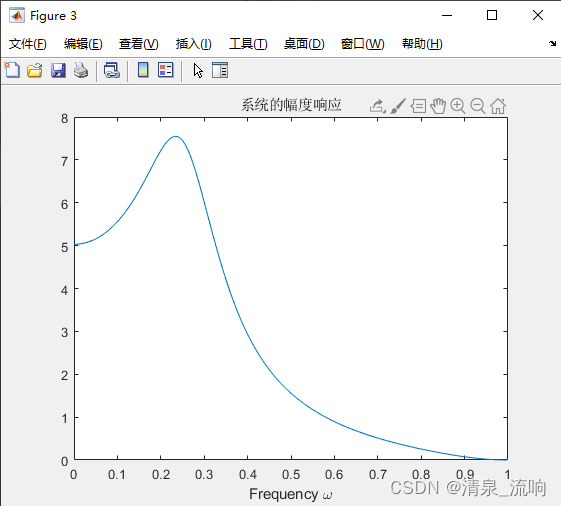
[H,w]=freqz(num,den);
figure;
plot(w/pi,abs(H));
xlabel('Frequency omega');
title('系统的幅度响应');

运行结果如下：

最后

以上就是尊敬冰淇淋为你收集整理的信号与系统的仿真习题五的全部内容，希望文章能够帮你解决信号与系统的仿真习题五所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。