概述
在频谱中低频主要对应图像在平滑区域的总体灰度级分布，而高频对应图像的细节部分，如边缘和噪声。因此图像平滑可以通过衰减图像频谱中的高频部分来实现，这就建立了空间域图像平滑和频域低通滤波之间的对应关系。
理论基础
最容易想到的衰减高频成分方法是在一个称为‘截止频率’的位置截断所有的高频成分，将图像频谱中所有高于这一截止的频谱 成分设为0，低于截止频率的成分设为保持不变。能够达到这种效果的滤波器我们称之为理想低通滤波器。如果图像的宽度为 M，高度为N,那么理想的低通频域滤波器可以形式化的描述为
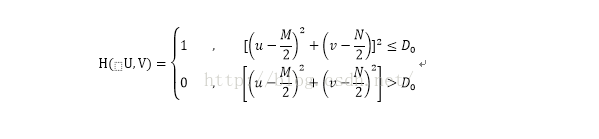
其中D0表示理想低通滤波器的截止频率，滤波器的频率域原点在频谱图像的中心处，在以截止频率为半径的圆形区域 之内的滤镜元素值全部为1，而该圆之外的滤镜元素值全部为0.理想低通滤波器的频率特性在截止频率处十分陡峭，无法用硬件实现，这也是我们称之为理想的原因，但其软件编程的模拟实现较为简单。
理想低通滤波器可以在一定程度上去除图像噪声，但由此带来的图像边缘和细节的模糊效应也比较明显，其滤波之后的处理效果比较类似于平均模板的平均平滑，实际上，理想低通滤波器是一个与频谱图像同样尺寸的二维矩阵，通过将矩阵中对应较高频率的部分设为0，较低频率的部分设为1，可在与频谱图像相乘后有效去除频谱的高频部分，其中0和1的交界处即对应滤波器的截止频率。
我们用imidealflpf 函数可以得到截止频率
最后
以上就是成就纸鹤为你收集整理的频域低通滤波器（MATLAB 含代码）的全部内容，希望文章能够帮你解决频域低通滤波器（MATLAB 含代码）所遇到的程序开发问题。
如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。
本图文内容来源于网友提供，作为学习参考使用，或来自网络收集整理，版权属于原作者所有。
发表评论 取消回复