控制系统Matlab仿真——数学模型

一、拉氏变换

如果用微分方程描述系统模型，求解会变得困难。而把微分方程转换为拉氏变换后，再求解则变得相对容易。

求的拉氏变换

clear;close all;clc;
syms t s; %定义符号
D = t^2*exp(-t); %表达式
MS = laplace(D,t,s); %拉氏变换
pretty(MS) %按数学的习惯显示公式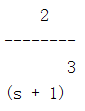

二、传递函数模型

clear;close all;clc;
num=[1 4 8]; %分子多项式
den=[1 11 11 10]; %分母多项式
G=tf(num,den) %传递函数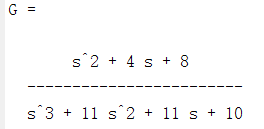

分子/分母多项式如果是乘积的形式，可以用conv()，conv()支持嵌套。

den=conv([1 11 11 10],[1,0]);

三、零极点模型

clear;close all;clc;
num=[1 4 8];
den=conv([1 11 11 10],[1,0]);
G=tf(num,den) %传递函数
[z,p,k]=tf2zp(num,den) %零极点和增益
[r,p,k]=residue(num,den) %部分分式

四、状态空间模型

clear;close all;clc;
A=[1 6 9 10;3 12 6 8;4 7 9 11;5 12 13 14];
B=[4 6;2 4;2 2;1 0];
C=[0 0 2 1;8 0 2 2];
D=zeros(2,2);
G=ss(A,B,C,D)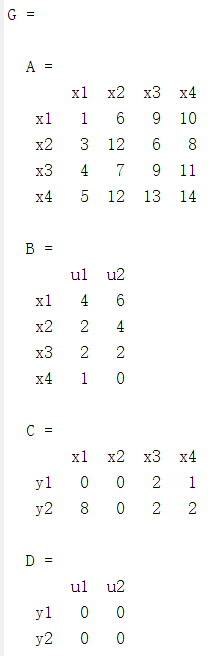

 五、模型的转换

clear;close all;clc;
z=[-2];p=[-1,-3,-5];k=6;
[num,den]=zp2tf(z,p,k) %零极点转传递函数
[A,B,C,D]=zp2ss(z,p,k) %零极点转状态空间
g_zpk=zpk(z,p,k) %零极点模型
g_tf=tf(num,den) %传递函数模型
g_ss=ss(A,B,C,D) %状态空间模型
%转换函数有：ss2tf,ss2zp,tf2zp,tf2ss,zp2ss,zp2tf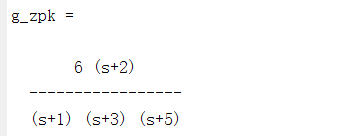

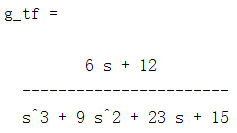
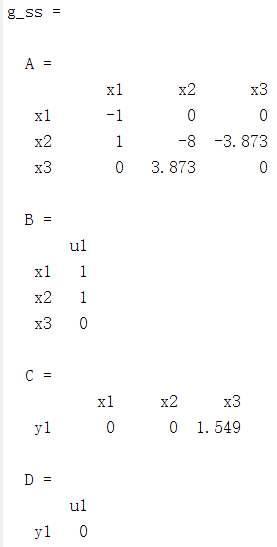
 六、模型的连接

clear;close all;clc;
num1=6*[1,2];
den1=conv([1,1],conv([1,3],[1,5]));
num2=[1,2.5];
den2=conv([1,1],[1,4]);
[nums,dens]=series(num1,den1,num2,den2); %串联
[nump,denp]=parallel(num1,den1,num2,den2); %并联
[numc,denc]=cloop(num1,den1); %闭环,H(s)=1
[numf,denf]=feedback(num1,den1,num2,den2); %反馈
s_tf=tf(nums,dens)
p_tf=tf(nump,denp)
c_tf=tf(numc,denc)
f_tf=tf(numf,denf)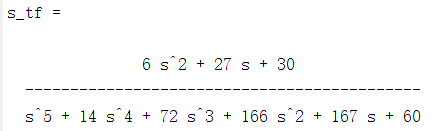

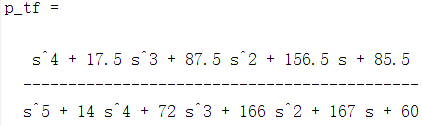
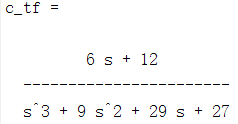
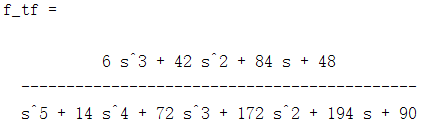
最后

以上就是魁梧胡萝卜为你收集整理的控制系统Matlab仿真——数学模型的全部内容，希望文章能够帮你解决控制系统Matlab仿真——数学模型所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。