概述
MATLAB笔记
1.MATLAB基本操作
1.1 续行符...
3个小黑点称为续行符，即把下面的物理行看做该行的逻辑继续。
例如：>> s=1-1/2+1/3-1/4+1/5-1/6+1/7-... 1/8+1/9-1/10+1/11-1/12;
1.2命令行的编辑
|
键名
|
功能
|
键名
|
功能
|
|
↑
|
前寻式调回已输入过的命令
|
Home
|
将光标移到当前行首端
|
|
↓
|
后寻式调回已输入过的命令
|
End
|
将光标移到当前行末尾
|
|
←
|
在当前行中左移光标
|
Del
|
删除光标右边的字符
|
|
→
|
在当前行中右移光标
|
Backspace
|
删除光标左边的字符
|
|
PgUp
|
前寻式翻滚一页
|
Esc
|
删除当前行的全部内容
|
|
PgDn
|
后寻式翻滚一页
|
Ctrl+C
|
中断一个
MATLAB
任务
|
1.3注释 ：%
注释以%开头，后面是注释的内容。
1.4 MATLAB帮助命令：
（1）help命令help命令是查询函数语法的最基本方法，查询信息直接显示在命令行窗口。
（2）lookfor命令help命令只搜索出那些关键字完全匹配的结果，lookfor命令对搜索范围内的M文件进行关键字搜索，条件比较宽松。
（3）模糊查询MATLAB提供了一种类似模糊查询的命令查询方法，用户只需要输入命令的前几个字母，然后按Tab键，系统就会列出所有以这几个字母开头的命令。
第2章 MATLAB数据及其运算
2.1.1 数值数据类型的分类
1．整型
|
类型
|
取值范围
|
转换函数
|
类型
|
取值范围
|
转换函数
|
|
无符号
8
位整型
|
0
到
2
8
-1
|
uint8
|
无符号
16
位整型
|
0
到
2
16
-1
|
uint16
|
|
无符号
32
位整型
|
0
到
2
32
-1
|
uint32
|
无符号
64
位整型
|
0
到
2
64
-1
|
uint64
|
|
带符号
8
位整型
|
-2
7
到
2
7
-1
|
int8
|
带符号
16
位整型
|
-2
15
到
2
15
-1
|
int16
|
|
带符号
32
位整型
|
-2
31
到
2
31
-1
|
int32
|
带符号
64
位整型
|
-2
63
到
2
63
-1
|
int64
|
2．浮点型
浮点型数据有单精度（single）和双精度（double）之分，单精度型实数在内存中占用4个字节，双精度型实数在内存中占用8个字节，双精度型的数据精度更高。在MATLAB中，数据默认为双精度型。single函数可以将其他类型的数据转换为单精度型，double函数可以将其他类型的数据转换为双精度型
3．复型
复型数据包括实部和虚部两个部分，实部和虚部默认为双精度型。在MATLAB中，虚数单位用i或j表示。例如，6+5i与6+5j表示的是同一个复数，也可以写成6+5*i或6+5*j，这里将i或j看作一个运算量参与表达式的运算。
2.1.2 数据的输出格式
format命令的格式
|
格式符
|
含义
|
|
short
|
输出小数点后
4
位，最多不超过
7
位有效数字。对于大于
1000
的实数，用
5
位有效数字的科学记数形式输出
|
|
long
|
15
位有效数字形式输出
|
|
short e
|
5
位有效数字的科学记数形式输出
|
|
long e
|
15
位有效数字的科学记数形式输出
|
|
short g
|
从
short
和
short e
中自动选择最佳输出方式
|
|
long g
|
从
long
和
long e
中自动选择最佳输出方式
|
|
rat
|
近似有理数表示
|
|
hex
|
十六进制表示
|
|
+
|
正数、负数、零分别用
+
、
-
、空格表示
|
|
bank
|
银行格式，用元、角、分表示
|
|
compact
|
输出变量之间没有空行
|
|
loose
|
输出变量之间有空行
|
2.2 MATLAB矩阵的表示
>> A=[1,2,3;4,5,6;7,8,9];
>> B=[-1,-2,-3;-4,-5,-6;-7,-8,-9];
>> C=[A,B;B,A] C = 1 2 3 -1 -2 -3 4 5 6 -4 -5 -6 7 8 9 -7 -8 -9 -1 -2 -3 1 2 3 -4 -5 -6 4 5 6 -7 -8 -9 7 8 9
2.2.2 冒号表达式
冒号表达式可以产生一个行向量，一般格式是： e1:e2:e3其中e1为初始值，e2为步长，e3为终止值。
在MATLAB中，还可以用linspace函数产生行向量。其调用格式为：linspace(a,b,n)其中a和b是生成向量的第一个和最后一个元素，n是元素总数。显然，linspace(a,b,n)与a:(b-a)/(n-1):b等价。
2.2.3 矩阵的引用
A(3,2)=200
2. 利用冒号表达式获得子矩阵
① A(:,j)表示取A矩阵的第j列全部元素；A(i,:)表示A矩阵第i行的全部元素；A(i,j)表示取A矩阵第i行、第j列的元素。
② A(i:i+m,:)表示取A矩阵第i～i+m行的全部元素；A(:,k:k+m)表示取A矩阵第k～k+m列的全部元素，A(i:i+m,k:k+m)表示取A矩阵第i～i+m行内，并在第k～k+m列中的所有元素。
③A(:)将矩阵A每一列元素堆叠起来，成为一个列向量，而这也是MATLAB变量的内部储存方式。
end表示某一维的末尾元素下标。
3.利用空矩阵删除矩阵的元素
在MATLAB中，定义[]为空矩阵。给变量X赋空矩阵的语句为X=[]。注意，X=[]与clear X不同，clear是将X从工作空间中删除，而空矩阵则存在于工作空间中，只是维数为0。
4．改变矩阵的形状
reshape(A,m,n)函数在矩阵总元素保持不变的前提下，将矩阵A重新排成m×n的二维矩阵。
例如：
>> x=[23,45,65,34,65,34,98,45,78,65,43,76]
>> y=reshape(x,3,4)
y = 23 34 98 65
45 65 45 43
65 34 78 76
注意：reshape函数只是改变原矩阵的行数和列数，即改变其逻辑结构，但并不改变原矩阵元素个数及其存储顺序。A(:)将矩阵A的每一列元素堆叠起来，成为一个列向量，从而改变了矩阵的形状。
2.3 变量及其操作
2.3.1 变量与赋值语句
赋值语句(1) 变量=表达式 (2) 表达式
2.3.2预定义变量
用pi表示圆周率π的近似值，用i，j表示虚数单位。
2.4 MATLAB常用内部函数
|
函数名
|
功能
|
函数名
|
功能
|
|
sin/
sind
|
正弦函数，输入值为弧度
/
角度
|
abs
|
绝对值函数
|
|
cos
/
cosd
|
余弦函数，输入值为弧度
/
角度
|
rem
|
求余
|
|
tan/
tand
|
正切函数，输入值为弧度
/
角度
|
mod
|
求模
|
|
asin/asind
|
反正弦函数，返回值为弧度
/
角度
|
fix
|
向零方向取整
|
|
acos/acosd
|
反余弦函数，返回值为弧度
/
角度
|
floor
|
不大于自变量的最大整数
|
|
atan/atand
|
反正切函数，返回值为弧度
/
角度
|
ceil
|
不小于自变量的最小整数
|
|
sinh/asinh
|
双曲正弦函数
/
反双曲正弦函数
|
round
|
四舍五入到最邻近的整数
|
|
cosh/acosh
|
双曲余弦函数
/
反双曲余弦函数
|
sign
|
符号函数
|
|
tanh/atanh
|
双曲正切函数
/
反双曲正切函数
|
gcd
|
最大公约数
|
|
sqrt
|
平方根函数
|
lcm
|
最小公倍数
|
|
log
|
自然对数函数
|
factor
|
返回自变量的全部素数因子
|
|
log10
|
常用对数函数
|
factorial
|
阶乘
|
|
log2
|
以
2
为底的对数函数
|
isprime
|
判断是否为素数
|
|
exp
|
自然指数函数
|
primes
|
生成素数列表
|
|
pow2
|
2
的幂
|
perms
|
生成所有排列
|
2.4.2 矩阵的超越函数（参数A必须是方阵）
1．矩阵平方根sqrtm(A)计算矩阵A的平方根。
例如：
>> A=[4,2;3,6];
>> B=sqrtm(A)
B = 1.9171 0.4652 0.6978 2.3823
2．矩阵对数
logm(A)计算矩阵A的自然对数。
例如：>> A=[4,9;1,5]; >> L=logm(A) L = 1.0639 2.4308 0.2701 1.3340
3．矩阵指数
例如，对上面计算所得到的A的自然对数L，求其矩阵指数B= eL：>> B=expm(L) B = 4.0000 9.0000 1.0000 5.0000
4．普通矩阵函数
funm(A,@fun)对方阵A计算由fun定义的函数的矩阵函数值。
例如，当fun取exp时，funm(A,@exp)可以计算矩阵A的指数，与expm(A)的计算结果一样。
>> A=[2,-1;1,0];
>> funm(A,@exp)
ans =
5.4366 -2.7183
2.7183 0.0000
>> expm(A)
ans =
5.4366 -2.7183
2.7183 0
2.5 MATLAB运算
2.5.1 算术运算
＋(加)、－(减)、*(乘)、/(右除)、(左除)、^(乘方)。
注意，运算是在矩阵意义下进行的，单个数据的算术运算只是一种特例。
(1) 矩阵加减运算
A+B和A-B（若A和B矩阵的维数相同，则可以执行矩阵的加减运算）
(2) 矩阵乘法
假定有两个矩阵A和B，若A为m×n矩阵，B为n×p矩阵，则C=A*B为m×p矩阵。
(3) 矩阵除法
在MATLAB中，有两种矩阵除法运算：和/，分别表示左除和右除。如果A矩阵是非奇异方阵，则AB和B/A运算可以实现。AB等效于A的逆左乘B矩阵，也就是inv(A)*B，而B/A等效于A矩阵的逆右乘B矩阵，也就是B*inv(A)。
(4) 矩阵的乘方
一个矩阵的乘方运算可以表示成A^x，要求A为方阵，x为标量。
2．点运算
在MATLAB中，有一种特殊的运算，因为其运算符是在有关算术运算符前面加点，所以叫点运算。点运算符有.*、./、.和.^。两矩阵进行点运算是指它们的对应元素进行相关运算，要求两矩阵的维参数相同。
2.5.2 关系运算
<(小于)、<=(小于或等于)、>(大于)、>=(大于或等于)、==(等于)、～=(不等于)。
例2-3 建立5阶方阵A，判断A的元素是否能被3整除。 A =[24,35,13,22,63;23,39,47,80,80; ... 90,41,80,29,10;45,57,85,62,21;37,19,31,88,76]; P=rem(A,3)==0 P = 1 0 0 0 1 0 1 0 0 0 1 0 0 0 0 1 1 0 0 1 0 0 0 0 0 其中，rem(A,3)是矩阵A的每个元素除以3的余数矩阵。此时，0被扩展为与A同维数的零矩阵，P是进行等于(==)比较的结果矩阵。
2.5.3 逻辑运算
&(与)、|(或)和～(非)。
2.6 字符串
例2-5 建立一个字符串向量，然后对该向量做如下处理：(1) 取第1～5个字符组成的子字符串。(2) 将字符串倒过来重新排列。(3) 将字符串中的小写字母变成相应的大写字母，其余字符不变。(4) 统计字符串中小写字母的个数。
命令如下：ch=‘ABc123d4e56Fg9’;
subch=ch(1:5) %取子字符串
revch=ch(end:-1:1) %将字符串倒排
k=find(ch>=‘a’&ch<=‘z’); %找小写字母的位置
ch(k)=ch(k)-(‘a’-‘A’); %将小写字母变成相应的大写字母
char(ch)
length(k) %统计小写字母的个数
2.6.2 字符串的操作
1．字符串的执行
eval函数：
eval(s)其中s为字符串。
例如：
>> t=pi;
>> m='[t,sin(t),cos(t)]';
>> y=eval(m) y = 3.1416 0.0000 -1.0000
2.字符串的连接
在MATLAB中，要将两个字符串连接在一起，有两种常见方法：一是用字符串向量，二是用strcat函数。
3.字符串的比较
当两个字符串拥有相同的长度时，可以利用关系运算符对字符串进行比较
例如：>> 'www0'>='W123' ans = 1 1 1 0
字符串比较函数用于判断字符串是否相等，有4种比较方式，函数如下：
① strcmp(s1,s2)：用来比较字符串s1和s2是否相等，如果相等，返回1，否则返回0。
② strncmp(s1,s2,n)：用来比较前n个字符是否相等，如果相等，返回1，否则返回0。
③ strcmpi(s1,s2)：在忽略字母大小写前提下，比较字符串s1和s2是否相等，如果相等，返回1，否则返回0。
④ strncmpi(s1,s2,n)：在忽略字符串大小写前提下，比较前n个字符是否相等，如果相等，返回1，否则返回0
2.7 结构数据和单元数据
1．结构矩阵的建立与引用建立一个结构矩阵可采用给结构成员赋值的办法。
具体格式为：结构矩阵名.成员名=表达式其中表达式应理解为矩阵表达式。
2．结构成员的修改可以根据需要增加或删除结构的成员。例如要给结构矩阵a增加一个成员x4，可给a中任意一个元素增加成员x4：a(1).x4=‘410075’;但其他成员均为空矩阵，可以使用赋值语句给它赋确定的值。要删除结构的成员，则可以使用rmfield函数来完成。例如，删除成员x4：a=rmfield(a,‘x4’);
2.7.2 单元数据
建立单元矩阵和一般矩阵相似，只是矩阵元素用大括号括起来。可以用带有大括号下标的形式引用单元矩阵元素。例如b{3,3}。单元矩阵的元素可以是结构或单元数据。可以使用celldisp函数来显示整个单元矩阵，如celldisp(b)
第3章 MATLAB矩阵分析与处理
3.1 特殊矩阵
常用的产生通用特殊矩阵的函数有：
zeros：产生全0矩阵(零矩阵)。
ones：产生全1矩阵(幺矩阵)。
eye：产生单位矩阵。
rand：产生0～1区间均匀分布的随机矩阵。
randn：产生均值为0，方差为1的标准正态分布随机矩阵。
例3-1
建立随机矩阵：
(1) 在区间[20,50]内均匀分布的5阶随机矩阵。
(2) 均值为0.6、方差为0.1的5阶正态分布随机矩阵。
分析：产生(0，1)区间均匀分布随机矩阵使用rand函数，假设得到了一组满足(0，1)区间均匀分布的随机数xi，则若想得到在任意[a，b]区间上均匀分布的随机数，只需用yi=a+(b-a)xi计算即可。产生均值为0、方差为1的标准正态分布随机矩阵使用randn函数，假设已经得到了一组标准正态分布随机数xi，如果想更一般地得到均值为μ、方差为σ2的随机数，可用yi=μ+σxi计算出来。
>> x=20+(50-20)*rand(5)
x = 44.4417 22.9262 24.7284 24.2566 39.6722
47.1738 28.3549 49.1178 32.6528 21.0714
23.8096 36.4064 48.7150 47.4721 45.4739
47.4013 48.7252 34.5613 43.7662 48.0198
38.9708 48.9467 44.0084 48.7848 40.3621
>> y=0.6+sqrt(0.1)*randn(5)
y = 0.9272 0.8809 1.0549 0.5677 0.5905
0.8299 0.2373 0.7028 0.5236 0.5479
0.5040 0.2620 0.3613 0.7009 0.7985
0.6929 0.3440 1.0333 0.6989 0.9457
0.3510 -0.3311 0.0588 0.3265 0.9508
3.1.2 用于专门学科的特殊矩阵
(1) 魔方矩阵
魔方矩阵有一个有趣的性质，其每行、每列及两条对角线上的元素和都相等。对于n阶魔方阵，其元素由1,2,3,…,n2共n2个整数组成。
求魔方矩阵的函数magic(n)，其功能是生成一个n阶魔方阵。
例3-2 将101~125等25个数填入一个5行5列的表格中，使其每行每列及对角线的和均为565。
M=100+magic(5)
M =
117 124 101 108 115
123 105 107 114 116
104 106 113 120 122
110 112 119 121 103
111 118 125 102 109
(2) 范得蒙矩阵
范得蒙(Vandermonde)矩阵最后一列全为1，倒数第二列为一个指定的向量，其他各列是其后列与倒数第二列的点乘积。
函数vander(V)生成以向量V为基础向量的范得蒙矩阵。
A=vander([1;2;3;5])
A = 1 1 1 1
8 4 2 1
27 9 3 1
125 25 5 1
(3) 希尔伯特矩阵
在MATLAB中，生成希尔伯特矩阵的函数是hilb(n)使用一般方法求逆会因为原始数据的微小扰动而产生不可靠的计算结果。
MATLAB中，有一个专门求希尔伯特矩阵的逆的函数invhilb(n)，其功能是求n阶的希尔伯特矩阵的逆矩阵。
例3-3 求4阶希尔伯特矩阵及其逆矩阵。
命令如下：
format rat %以有理形式输出
H=hilb(4)H = 1 1/2 1/3 1/4
1/2 1/3 1/4 1/5
1/3 1/4 1/5 1/6
1/4 1/5 1/6 1/7
H=invhilb(4)
H =
16 -120 240 -140
-120 1200 -2700 1680
240 -2700 6480 -4200
-140 1680 -4200 2800
(4) 托普利兹矩阵
托普利兹(Toeplitz)矩阵除第一行第一列外，其他每个元素都与左上角的元素相同。生成托普利兹矩阵的函数是toeplitz(x,y)，它生成一个以x为第一列，y为第一行的托普利兹矩阵。这里x, y均为向量，两者不必等长。toeplitz(x)用向量x生成一个对称的托普利兹矩阵。
例如T1=toeplitz(1:6) T2=toeplitz(1:4,1:5)
>> toeplitz(1:4)
ans =
1 2 3 4
2 1 2 3
3 2 1 2
4 3 2 1
>> toeplitz(1:4,1:5)
ans =
1 2 3 4 5
2 1 2 3 4
3 2 1 2 3
4 3 2 1 2
(5) 伴随矩阵
MATLAB生成伴随矩阵的函数是compan(p)，其中p是一个多项式的系数向量，高次幂系数排在前，低次幂排在后。
例如，为了求多项式的x3-7x+6的伴随矩阵，可使用命令：p=[1,0,-7,6];compan(p)
>> p=[1,0,-7,6];compan(p)
ans =
0 7 -6
1 0 0
0 1 0
(6) 帕斯卡矩阵
我们知道，二次项(x+y)n展开后的系数随n的增大组成一个三角形表，称为杨辉三角形。由杨辉三角形表组成的矩阵称为帕斯卡(Pascal)矩阵。函数pascal(n)生成一个n阶帕斯卡矩阵。
>> pascal(5)
ans =
1 1 1 1 1
1 2 3 4 5
1 3 6 10 15
1 4 10 20 35
1 5 15 35 70
3.2 矩阵变换
3.2.1 对角阵与三角阵
1．对角阵
只有对角线上有非0元素的矩阵称为对角矩阵，对角线上的元素相等的对角矩阵称为数量矩阵，对角线上的元素都为1的对角矩阵称为单位矩阵。
(1) 提取矩阵的对角线元素设A为m×n矩阵，diag(A)函数用于提取矩阵A主对角线元素，产生一个具有min(m,n)个元素的列向量。diag(A)函数还有一种形式diag(A,k)，其功能是提取第k条对角线的元素。
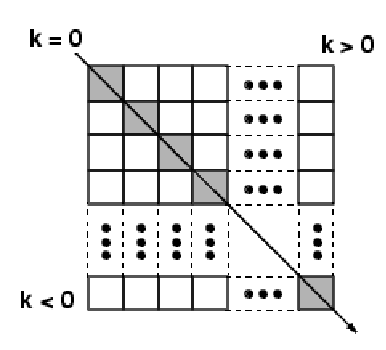
>> diag([1:2:9])
ans =
1 0 0 0 0
0 3 0 0 0
0 0 5 0 0
0 0 0 7 0
0 0 0 0 9
>> diag([1:2:9],1)
ans =
0 1 0 0 0 0
0 0 3 0 0 0
0 0 0 5 0 0
0 0 0 0 7 0
0 0 0 0 0 9
0 0 0 0 0 0
(2) 构造对角矩阵设V为具有m个元素的向量，diag(V)将产生一个m×m对角矩阵，其主对角线元素即为向量V的元素。
diag(V)函数也有另一种形式diag(V,k)，其功能是产生一个n×n(n=m+|k|)对角阵，其第k条对角线的元素即为向量V的元素。
>> V=[1,4,7,2,5,8]
V =
1 4 7 2 5 8
>> diag(V)
ans =
1 0 0 0 0 0
0 4 0 0 0 0
0 0 7 0 0 0
0 0 0 2 0 0
0 0 0 0 5 0
0 0 0 0 0 8
>> diag(V,1)
ans =
0 1 0 0 0 0 0
0 0 4 0 0 0 0
0 0 0 7 0 0 0
0 0 0 0 2 0 0
0 0 0 0 0 5 0
0 0 0 0 0 0 8
0 0 0 0 0 0 0
例3-5 先建立5×5矩阵A，然后将A的第一行元素乘以1，第二行乘以2，…，第五行乘以5。
A=[17,0,1,0,15;23,5,7,14,16;4,0,13,0,22;10,12,19,21,3;...11,18,25,2,19];D=diag(1:5);
D*A %用D左乘A，对A的每行乘以一个指定常数
>> D=diag(1:5)
D =
1 0 0 0 0
0 2 0 0 0
0 0 3 0 0
0 0 0 4 0
0 0 0 0 5
>> A=[17,0,1,0,15;23,5,7,14,16;4,0,13,0,22;10,12,19,21,3;...11,18,25,2,19];
>> D*A
ans =
17 0 1 0 15
46 10 14 28 32
12 0 39 0 66
40 48 76 84 12
55 90 125 10 95
2．三角阵
三角阵又进一步分为上三角阵和下三角阵，所谓上三角阵，即矩阵的对角线以下的元素全为0的一种矩阵，而下三角阵则是对角线以上的元素全为0的一种矩阵。
(1) 上三角矩阵求矩阵A的上三角阵的MATLAB函数是triu(A)。triu(A)函数也有另一种形式triu(A,k)，其功能是求矩阵A的第k条对角线以上的元素。例如，提取矩阵A的第2条对角线以上的元素，形成新的矩阵B。
(2) 下三角矩阵在MATLAB中，提取矩阵A的下三角矩阵的函数是tril(A)和tril(A,k)，其用法与提取上三角矩阵的函数triu(A)和triu(A,k)完全相同
ans =
1 1 1 1
1 1 1 1
1 1 1 1
1 1 1 1
>> triu(ans)
ans =
1 1 1 1
0 1 1 1
0 0 1 1
0 0 0 1
>> triu(ans,1)
ans =
0 1 1 1
0 0 1 1
0 0 0 1
0 0 0 0
下三角阵和上的用法一样
3.2.2 矩阵的转置与旋转
1．矩阵的转置
转置运算符是小数点后面接单引号（.'）。
还有一种转置叫共轭转置，其运算符是单引号（'），它在转置的基础上还要取每个数的复共轭。
例如，B=A'得到的B就是A的共轭转置矩阵，等价于B=conj(A).'或B=conj(A.')。
如果矩阵的元素都是实数，那么转置和共轭转置的结果是一样的。
2．矩阵的旋转
利用函数rot90(A,k)将矩阵A旋转90º的k倍，当k为1时可省略。
3．矩阵的左右翻转
对矩阵实施左右翻转是将原矩阵的第一列和最后一列调换，第二列和倒数第二列调换，…，依次类推。
MATLAB对矩阵A实施左右翻转的函数是fliplr(A)。
4．矩阵的上下翻转
MATLAB对矩阵A实施上下翻转的函数是flipud(A)。
3.2.3 矩阵的逆与伪逆
1.矩阵的逆
对于一个方阵A，如果存在一个与其同阶的方阵B，使得：A·B=B·A=I (I为单位矩阵)则称B为A的逆矩阵，当然，A也是B的逆矩阵。
求一个矩阵的逆是一件非常烦琐的工作，容易出错，但在MATLAB中，求一个矩阵的逆非常容易。求方阵A的逆矩阵可调用函数inv(A)。
如果矩阵A不是一个方阵，或者A是一个非满秩的方阵时，矩阵A没有逆矩阵，但可以找到一个与A的转置矩阵A‘同型的矩阵B，使得：A·B·A=AB·A·B=B此时称矩阵B为矩阵A的伪逆，也称为广义逆矩阵。在MATLAB中，求一个矩阵伪逆的函数是pinv(A)。
2 用矩阵求逆方法求解线性方程组
在线性方程组Ax=b两边各左乘A-1，有 A-1Ax=A-1b 由于A-1A=I，故得 x=A-1b 例3-7 用求逆矩阵的方法解线性方程组。
命令如下：
A=[1,2,3;1,4,9;1,8,27];
b=[5,-2,6]';
x=inv(A)*b
x =
23
-29/2
11/3
也可以运用左除运算符“＼”求解线性代数方程组。
3．矩阵的伪逆
如果矩阵A不是一个方阵，或者A是一个非满秩的方阵时，矩阵A没有逆矩阵，但可以找到一个与A的转置矩阵A'同型的矩阵B，使得： A·B·A=A B·A·B=B 此时称矩阵B为矩阵A的伪逆，也称为广义逆矩阵。在MATLAB中，求一个矩阵伪逆的函数是pinv(A)。
3.3 矩阵求值
3.3.1 方阵的行列式
把一个方阵看作一个行列式，并对其按行列式的规则求值，这个值就称为所对应的行列式的值。
在MATLAB中，求方阵A所对应的行列式的值的函数是det(A)。
3.3.2 矩阵的秩与迹
1．矩阵的秩矩阵线性无关的行数与列数称为矩阵的秩。
在MATLAB中，求矩阵秩的函数是rank(A)。
2．矩阵的迹矩阵的迹等于矩阵的对角线元素之和，也等于矩阵的特征值之和。
在MATLAB中，求矩阵的迹的函数是trace(A)。
3.3.3 向量和矩阵的范数
矩阵或向量的范数用来度量矩阵或向量在某种意义下的长度。范数有多种方法定义，其定义不同，范数值也就不同。
1．向量的3种常用范数及其计算函数在MATLAB中，求向量范数的函数为：
(1) norm(V)或norm(V,2)：计算向量V的2—范数。
(2) norm(V,1)：计算向量V的1—范数。
(3) norm(V,inf)：计算向量V的∞—范数。
2．矩阵的范数及其计算函数
MATLAB提供了求3种矩阵范数的函数，其函数调用格式与求向量的范数的函数完全相同。
3.3.4 矩阵的条件数
在MATLAB中，计算矩阵A的3种条件数的函数是：(1) cond(A,1) 计算A的1—范数下的条件数。(2) cond(A)或cond(A,2) 计算A的2—范数数下的条件数。(3) cond(A,inf) 计算A的 ∞—范数下的条件数。
3.4 矩阵的特征值与特征向量
在MATLAB中，计算矩阵A的特征值和特征向量的函数是eig(A)，常用的调用格式有3种：
(1) E=eig(A)：求矩阵A的全部特征值，构成向量E。
(2) [V,D]=eig(A)：求矩阵A的全部特征值，构成对角阵D，并求A的特征向量构成V的列向量。
(3) [V,D]=eig(A,‘nobalance’)：与第2种格式类似，但第2种格式中先对A作相似变换后求矩阵A的特征值和特征向量，而格式3直接求矩阵A的特征值和特征向量。
(4) 可用A*V和V*D来验证结果。
例3-8 用求特征值的方法解方程。3x5-7x4+5x2+2x-18=0
p=[3,-7,0,5,2,-18];
A=compan(p); %A的伴随矩阵
x1=eig(A) %求A的特征值
x1 = 2.1837 + 0.0000i
1.0000 + 1.0000i
1.0000 - 1.0000i
-0.9252 + 0.7197i
-0.9252 - 0.7197i
x2=roots(p) %直接求多项式p的零点
3.5 稀疏矩阵
3.5.1 矩阵存储方式
MATLAB的矩阵有两种存储方式：完全存储方式和稀疏存储方式。
1．完全存储方式 完全存储方式是将矩阵的全部元素按列存储。
2．稀疏存储方式稀疏存储方式仅存储矩阵所有的非零元素的值及其位置，即行号和列号。
在MATLAB中，稀疏存储方式也是按列存储的。设：
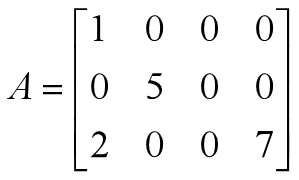
A是具有稀疏特征的矩阵，其完全存储方式是按列存储全部12个元素：1、0、2、0、5、0、0、0、0、0、0、7，其稀疏存储方式如下：(1，1)，1，(3，1)，2，(2，2)，5，(3，4)，7 括号内为元素的行列位置，其后面为元素值。
1．将完全存储方式转化为稀疏存储方式函数A=sparse(S)将矩阵S转化为稀疏存储方式的矩阵A。
当矩阵S是稀疏存储方式时，则函数调用相当于A=S。
ans =
1 0 0 0 0
0 1 0 0 0
0 0 1 0 0
0 0 0 1 0
0 0 0 0 1
>> sparse(ans)
ans =
(1,1) 1
(2,2) 1
(3,3) 1
(4,4) 1
sparse函数还有其他一些调用格式。
① sparse(m,n)：生成一个m×n的所有元素都是0的稀疏矩阵。
② sparse(u,v,S)：其中u、v、S是3个等长的向量。
S是要建立的稀疏矩阵的非零元素，u(i)、v(i)分别是S(i)的行和列下标，该函数建立一个max(u)行、max(v)列并以S为稀疏元素的稀疏矩阵。
此外，还有一些和稀疏矩阵操作有关的函数。
例如：① [u,v,S]=find(A)：返回矩阵A中非零元素的下标和元素。这里产生的u、v、S可作为sparse(u,v,S)的参数。
② full(A)：返回和稀疏存储矩阵A对应的完全存储方式矩阵。
2．产生稀疏存储矩阵
调用格式为：B=spconvert(A) 其中，A为一个m×3或m×4的矩阵，其每行表示一个非零元素，m是非零元素的个数
3．带状稀疏存储矩阵
spdiags函数的其他调用格式有：
① [B,d]=spdiags(A)：从原带状矩阵A中提取全部非零对角线元素赋给矩阵B及其这些非零对角线的位置向量d。
② B=spdiags(A,d)：从原带状矩阵A中提取由向量d所指定的那些非零对角线元素构成的矩阵B。
③ E=spdiags(B,d,A)：在原带状矩阵A中将由向量d所指定的那些非零对角线元素用矩阵B替代，构成一个新的带状矩阵E。若赋值号左边改为A，则矩阵A为经过替换后的新稀疏矩阵。
4．单位矩阵的稀疏存储单位矩阵只有对角线元素为1，其他元素都为0，是一种具有稀疏特征的矩阵。
3.5.3 稀疏矩阵应用举例
例3-11 求下列三对角线性方程组的解
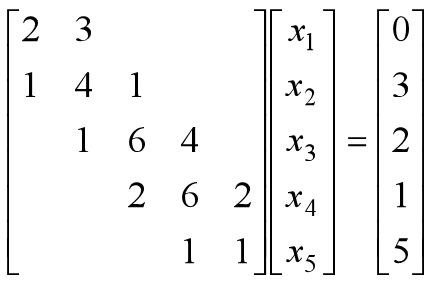
>> B=[1,2,0;1,4,3;2,6,1;1,6,4;0,1,2]; %产生非0对角元素矩阵
>> d=[-1;0;1] %产生非0对角元素位置向量
>> A=spdiags(B,d,5,5) %产生稀疏存储的系数矩阵
d =
-1
0
1
A =
(1,1) 2
(2,1) 1
(1,2) 3
(2,2) 4
(3,2) 1
(2,3) 1
(3,3) 6
(4,3) 2
(3,4) 4
(4,4) 6
(5,4) 1
(4,5) 2
(5,5) 1
第4章 MATLAB程序流程控制
4.1 M文件
M文件是一个文本文件，它可以用任何编辑程序来建立和编辑，而一般常用且最为方便的是使用MATLAB提供的文本编辑器。
1．建立新的M文件
为建立新的M文件，启动MATLAB编辑器有3种方法。
① 在MATLAB主窗口选择“主页”选项卡，在“文件”命令组中单击“新建脚本”命令按钮。
② 在MATLAB命令行窗口输入命令：edit 文件名 启动MATLAB编辑器后，输入M文件的内容并存盘。
③ 在命令历史窗口选中一些命令（按住Ctrl可同时选择多条命令），然后从右键快捷菜单中选择“创建脚本”命令，将会启动MATLAB编辑器，并在编辑区中加入所选中的命令。
2．打开已有的M文件
打开已有的M文件，也有3种方法：
(1) 菜单操作。在MATLAB主窗口选择“主页”选项卡，在“文件”命令组中单击“打开”命令按钮，再从弹出的下拉菜单中选择“打开”命令，从“打开”对话框中选择所需打开的M文件。
(2) 命令操作。在MATLAB命令窗口输入命令：edit 文件名，则打开指定的M文件。
(3) 命令按钮操作。单击MATLAB主窗口工具栏上的Open File命令按钮，再从弹出的对话框中选择所需打开的M文件。
4.1.2 M文件的分类
用MATLAB语言编写的程序，称为M文件。
M文件可以根据调用方式的不同分为两类：脚本文件(Script File)和函数文件(Function File)。
脚本文件和函数文件的主要区别如下：
① 脚本文件没有输入参数，也不返回输出参数，而函数文件可以带输入参数，也可返回输出参数。
② 脚本文件对MATLAB工作空间中的变量进行操作，文件中所有命令的执行结果也完全返回到工作空间中，而函数文件中定义的变量为局部变量，当函数文件执行完毕时，这些变量被清除。
③ 脚本文件可以直接运行，在MATLAB命令行窗口输入脚本文件的名字，就会顺序执行脚本文件中的命令，而函数文件不能直接运行，而要以函数调用的方式来调用它。
例4-1
建立一个命令文件将变量a,b的值互换，然后运行该命令文件。
程序1：
首先建立命令文件并以文件名exch.m存盘：
clear;
a=1:10;
b=[11,12,13,14;15,16,17,18];
c=a;
a=b;
b=c;
a b
然后在MATLAB的命令窗口中输入exch，将会执行该命令文件。
程序2：
首先建立函数文件fexch.m：
function [a,b]=exch(a,b)
c=a;
a=b;
b=c;
然后在MATLAB的命令窗口调用该函数文件：
clear; x=1:10; y=[11,12,13,14;15,16,17,18]; [x,y]=fexch(x,y)
4.2 程序控制结构
1．数据的输入
从键盘输入数据，则可以使用input函数来进行，该函数的调用格式为：
A=input(提示信息，选项)；
其中提示信息为一个字符串，用于提示用户输入什么样的数据。
如果在input函数调用时采用's'选项，则允许用户输入一个字符串。
例如： xm=input('What''s your name?','s');
2．数据的输出
MATLAB提供的命令窗口输出函数主要有disp函数，其调用格式为
disp(输出项) 其中输出项既可以为字符串，也可以为矩阵。
例4-2 求一元二次方程ax2 +bx+c=0的根。
程序如下：
a=input('a=?');
b=input('b=?');
c=input('c=?');
d=b*b-4*a*c;
x=[(-b+sqrt(d))/(2*a),(-b-sqrt(d))/(2*a)];
disp(['x1=',num2str(x(1)),',x2=',num2str(x(2))]);
a=?1
b=?2
c=?1
x1=-1,x2=-1
3．程序的暂停
暂停程序的执行可以使用pause函数，其调用格式为：
pause(延迟秒数)
如果省略延迟时间，直接使用pause，则将暂停程序，直到用户按任一键后程序继续执行。
若要强行中止程序的运行可使用Ctrl+C命令。
4.2.2
选择结构
1．if语句
在MATLAB中，if语句有3种格式。
(1) 单分支if语句：
if 条件
语句组
end
当条件成立时，则执行语句组，执行完之后继续执行if语句的后继语句，若条件不成立，则直接执行if语句的后继语句。
(2) 双分支if语句：
if 条件
语句组1
else
语句组2
end
当条件成立时，执行语句组1，否则执行语句组2，语句组1或语句组2执行后，再执行if语句的后继语句。
例4-3
计算分段函数。
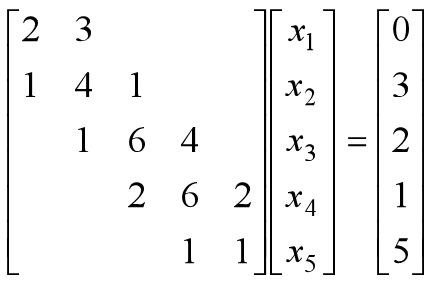
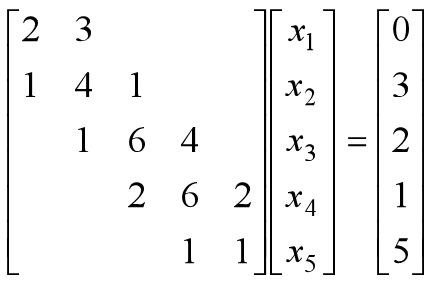
程序如下：
x=input('请输入x的值:');
if x==10
y=cos(x+1)+sqrt(x*x+1);
else
y=x*sqrt(x+sqrt(x)); end y
(3) 多分支if语句：
if 条件1
语句组1
elseif
条件2
语句组2
……
elseif
条件m
语句组m
else
语句组n
end
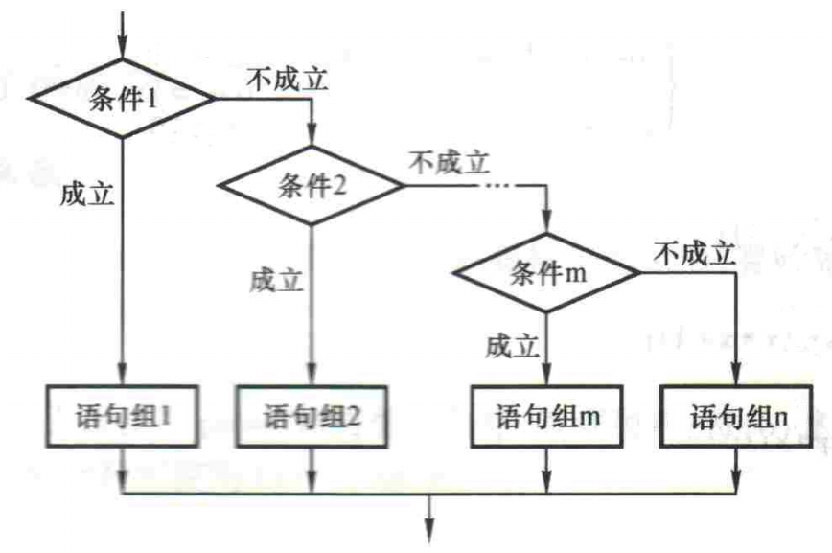
例4-4 输入一个字符，若为大写字母，则输出其对应的小写字母；若为小写字母，则输出其对应的大写字母；若为数字字符则输出其对应的数值的平方，若为其他字符则原样输出。
c=input('请输入一个字符','s');
if c>='A' & c<='Z'
disp(lower(c));
elseif c>='a'& c<='z'
disp(upper(c));
elseif c>='0'& c<='9'
disp(str2double(c)^2);
else
disp(c);
end
请输入一个字符a
A
2．switch语句
switch语句根据表达式的取值不同，分别执行不同的语句，其语句格式为：
switch 表达式
case 表达式1
语句组1
case 表达式2
语句组2
……
case 表达式m
语句组m
otherwise
语句组n
end
当表达式的值等于表达式1的值时，执行语句组1，当表达式的值等于表达式2的值时，执行语句组2，…，当表达式的值等于表达式m的值时，执行语句组m，当表达式的值不等于case所列的表达式的值时，执行语句组n。当任意一个分支的语句执行完后，直接执行switch语句的下一句。
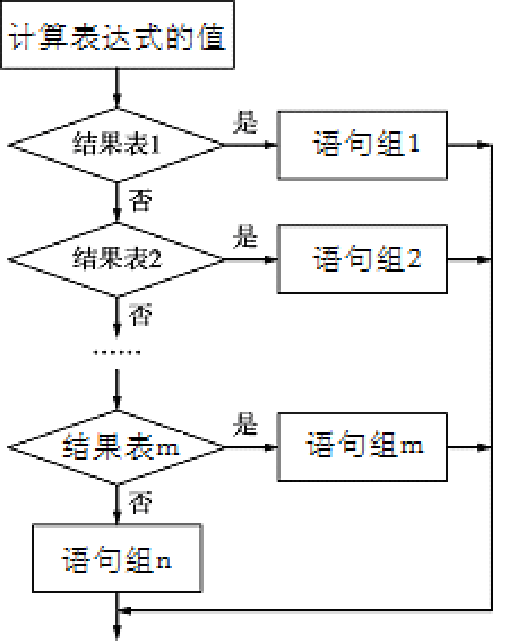
例4-5 某商场对顾客所购买的商品实行打折销售，标准如下(商品价格用price来表示)：
price<200 没有折扣
200≤price<500 3%折扣
500≤price<1000 5%折扣
1000≤price<2500 8%折扣
2500≤price<5000 10%折扣
5000≤price 14%折扣
输入所售商品的价格，求其实际销售价格。
price=input('请输入商品价格');
switch fix(price/100)
case {0,1} %价格小于200
rate=0;
case {2,3,4} %价格大于等于200但小于500
rate=3/100;
case num2cell(5:9) %价格大于等于500但小于1000
rate=5/100;
case num2cell(10:24) %价格大于等于1000但小于2500
rate=8/100;
case num2cell(25:49) %价格大于等于2500但小于5000
rate=10/100;
otherwise %价格大于等于5000
rate=14/100;
end
price=price*(1-rate) %输出商品实际销售价格
Num2cell()函数
num2cell的作用是把数值数组转换为cell数组最基本的用法是把数值数组的每个元素作为cell数组的元素，得到一个和原数组维度完全相同的cell数组，
例如：
>> A=magic(3)
A = 8 1 6 3 5 7 4 9 2
>> c=num2cell(A)
c = [8] [1] [6] [3] [5] [7] [4] [9] [2]
3．try语句语句
格式为：
try
语句组1 catch
语句组2
end
try语句先试探性执行语句组1，如果语句组1在执行过程中出现错误，则将错误信息赋给保留的lasterr变量，并转去执行语句组2。
例4-6
矩阵乘法运算要求两矩阵的维数相容，否则会出错。
先求两矩阵的乘积，若出错，则自动转去求两矩阵的点乘。
A=[1,2,3;4,5,6];
B=[7,8,9;10,11,12];
try
C=A*B;
catch
C=A.*B;
end C
lasterr %显示出错原因
4.2.3 循环结构
1．for语句
for语句的格式为：
for 循环变量=表达式1:表达式2:表达式3
循环体语句
end
其中，“表达式1:表达式2:表达式3”是一个冒号表达式，将产生一个行向量，3个表达式分别代表初值、步长和终值。
步长为1时，表达式2可以省略
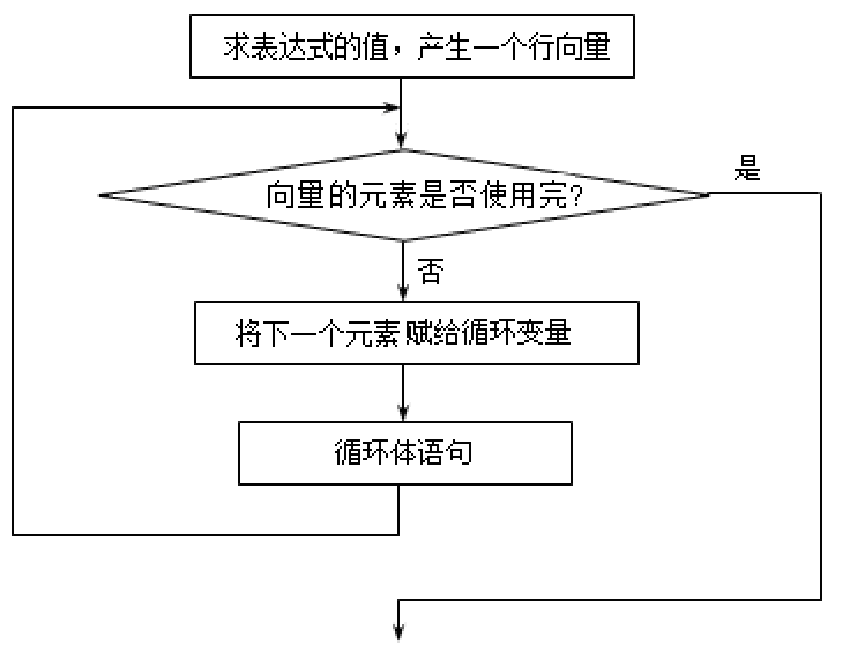
例4-7
一个三位整数各位数字的立方和等于该数本身则称该数为水仙花数。
输出全部水仙花数。
程序如下：
for m=100:999 m1=fix(m/100); %求m的百位数字
m2=rem(fix(m/10),10); %求m的十位数字
m3=rem(m,10); %求m的个位数字
if m==m1*m1*m1+m2*m2*m2+m3*m3*m3 disp(m)
end
end
153
370
371
407
例4-8 已知
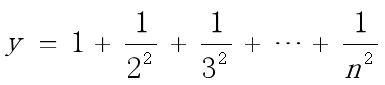当n=100时，求y的值。
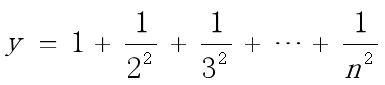当n=100时，求y的值。
程序如下： y=0;
n=100;
for i=1:n y=y+1/i/i;
end y
在实际MATLAB编程中，采用循环语句会降低其执行速度，所以前面的程序通常由下面的程序来代替：
n=100; i=1:n; f=1./i.^2; y=sum(f)
例4-9 设
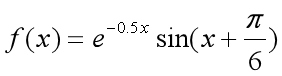，求 s= 以梯形法为例，
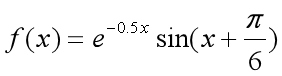，求 s= 以梯形法为例，
程序如下：
a=0;
b=3*pi;
n=1000;
h=(b-a)/n;
x=a; s=0;
f0=exp(-0.5*x)*sin(x+pi/6);
for i=1:n x=x+h;
f1=exp(-0.5*x)*sin(x+pi/6);
s=s+(f0+f1)*h/2;
f0=f1;
end
s
s =
754/837
for语句更一般的格式为：
for 循环变量=矩阵表达式
循环体语句
end
执行过程是依次将矩阵的各列元素赋给循环变量，然后执行循环体语句，直至各列元素处理完毕
例4-10 写出下列程序的执行结果。
s=0;
a=[12,13,14;15,16,17;18,19,20;21,22,23];
for k=a
s=s+k;
end
disp(s');
disp(s');
39 48 57 66
2．while语句
while语句的一般格式为：
while (条件)
循环体语句
end
其执行过程为：若条件成立，则执行循环体语句，执行后再判断条件是否成立，如果不成立则跳出循环。
例4-11
从键盘输入若干个数，当输入0时结束输入，求这些数的平均值和它们之和。
程序如下：
sum=0;
n=0;
val=input('Enter a number (end in 0):');
while (val~=0)
sum=sum+val;
n=n+1;
val=input('Enter a number (end in 0):');
end if (n > 0)
sum
mean=sum/n
end
例4-12 根据矩阵指数的幂级数展开式求矩阵指数。
程序如下：
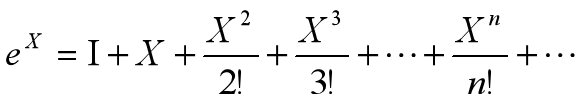
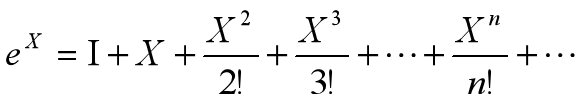
X=input('Enter X:');
E=zeros(size(X));
F=eye(size(X));
n=1;
while norm(F,1)>0
E=E+F;
F=F*X/n;
n=n+1;
end E expm(X)
3．break语句和continue语句
与循环结构相关的语句还有break语句和continue语句。它们一般与if语句配合使用。
break语句用于终止循环的执行。当在循环体内执行到该语句时，程序将跳出循环，继续执行循环语句的下一语句。
continue语句控制跳过循环体中的某些语句。当在循环体内执行到该语句时，程序将跳过循环体中所有剩下的语句，继续下一次循环。
例4-13 求[100，200]之间第一个能被21整除的整数。
程序如下：
for n=100:200
if rem(n,21)~=0 c
ontinue
end
break
end
n
4．循环的嵌套
如果一个循环结构的循环体又包括一个循环结构，就称为循环的嵌套，或称为多重循环结构。
例4-14 若一个数等于它的各个真因子之和，则称该数为完数，如6=1+2+3，所以6是完数。求[1,500]之间的全部完数。
for m=1:500 s=0;
for k=1:m/2
if rem(m,k)==0 s=s+k;
end
end
if m==s
disp(m);
end
end
例4-15
用筛选法求某自然数范围内的全部素数。
m=input('m=');
p=1:m; p(1)=0;
for i=2:sqrt(m) for j=2*i:i:m p(j)=0;
end
end
n=find(p~=0);
p(n)
4.3 函数文件
4.3.1
函数文件的基本结构
函数文件由function语句引导，其基本结构为：
function 输出形参表=函数名(输入形参表)
注释说明部分
函数体语句 其中以function开头的一行为引导行，表示该M文件是一个函数文件。
函数名的命名规则与变量名相同。
输入形参为函数的输入参数，输出形参为函数的输出参数。
当输出形参多于一个时，则应该用方括号括起来。
例4-16 编写函数文件求半径为r的圆的面积和周长。
函数文件如下：
function [s,p]=fcircle(r) %CIRCLE calculate the area and perimeter of a circle of radii r
%r 圆半径
%s 圆面积
%p 圆周长
%2006年2月30日编
s=pi*r*r;
p=2*pi*r;
4.3.2 函数调用
1.函数调用的一般格式是：
[输出实参表]=函数名(输入实参表)
要注意的是，函数调用时各实参出现的顺序、个数，应与函数定义时形参的顺序、个数一致，否则会出错。函数调用时，先将实参传递给相应的形参，从而实现参数传递，然后再执行函数的功能。
例4-17 利用函数文件，实现直角坐标(x,y)与极坐标(ρ,θ)之间的转换。
函数文件tran.m：
function [rho,theta]=tran(x,y)
rho=sqrt(x*x+y*y);
theta=atan(y/x);
调用tran.m的命令文件main1.m：
x=input('Please input x=:');
y=input('Please input y=:');
[rho,the]=tran(x,y);
rho
the
2．函数的递归调用在MATLAB中，函数可以嵌套调用，即一个函数可以调用别的函数，甚至调用它自身。一个函数调用它自身称为函数的递归调用。
例4-18 利用函数的递归调用，求n！。 n!本身就是以递归的形式定义的：
显然，求n!需要求(n-1)!，这时可采用递归调用。
递归调用函数文件factor.m如下：
function f=factor(n)
if n<=1
f=1;
else
f=factor(n-1)*n; %递归调用求(n-1)!
end
例4-19 任意排列问题。
MATLAB提供的函数randperm(n)，可以产生一个从整数1到整数n的任意排列。
编写一个函数来实现randperm(n)函数的功能，即给出一个由任意数组成的行向量，然后产生这个行向量元素的任意排列。
4.3.3 函数参数的可调性
在调用函数时，MATLAB用两个永久变量nargin和nargout分别记录调用该函数时的输入实参和输出实参的个数。只要在函数文件中包含这两个变量，就可以准确地知道该函数文件被调用时的输入输出参数个数，从而决定函数如何进行处理。
例4-20 nargin用法示例。
函数文件examp.m：
function fout=charray(a,b,c)
if nargin==1
fout=a;
elseif nargin==2
fout=a+b;
elseif nargin==3
fout=(a*b*c)/2;
end
命令文件mydemo.m：
x=[1:3];
y=[1;2;3];
examp(x)
examp(x,y')
examp(x,y,3)
4.3.4 全局变量与局部变量
函数文件中的变量是局部的，即在一个函数文件中定义的变量不能被另一个函数文件引用。如果在若干函数中都把某一变量定义为全局变量，那么这些函数将共用这个变量，作用域是整个工作空间，即全程有效。
全局变量用global命令定义，格式为： global 变量名
例4-21 全局变量应用示例。 先建立函数文件wadd.m，该函数将输入的参数加权相加。
function f=wadd(x,y)
global ALPHA BETA
f=ALPHA*x+BETA*y;
在命令窗口中输入： global ALPHA BETA
ALPHA=1;
BETA=2;
s=wadd(1,2)
4.4 特殊形式的函数
1. 子函数
在MATLAB中，可以在一个M文件中同时定义多个函数，其中M文件中出现的第一个函数称为主函数（primary function），其他函数称为子函数（subfunction），但需要注意的是子函数只能由同一M文件中的函数调用。在保存M文件时，M文件名一般和主函数名相同，外部程序只能对主函数进行调用。
2. 内联函数
以字符串形式存在的函数表达式可以通过inline函数转化成内联函数。
例如a='(x+y)^2'，可以通过f=inline(a)生成内联函数f(x,y)=(x+y)^2。
>> a='(x+y)^2';
>> f=inline(a) f =
内联函数:
f(x,y) = (x+y)^2
>> f(3,4)
ans =
49
3. 匿名函数
匿名函数的基本格式如下：
匿名函数名=@(输入参数) 匿名函数表达式 其中，匿名函数的输入参数可以是一个，也可以是多个，有多个参数时，参数间用逗号分隔。
例如：
>> f=@(x,y) x^2+y^2;
>> f(3,4)
ans =
25
4.5 程序调试与优化
*
4.5.1 程序调试方法 一般来说，应用程序的错误有两类，一类是语法错误，另一类是运行时的错误。语法错误包括词法或文法的错误，例如函数名的拼写错、表达式书写错等。
程序运行时的错误是指程序的运行结果有错误，这类错误也称为程序逻辑错误。
1．利用调试函数进行程序调试
2．利用调试工具进行程序调试
4.5.2
程序性能分析与优化
1．程序性能分析
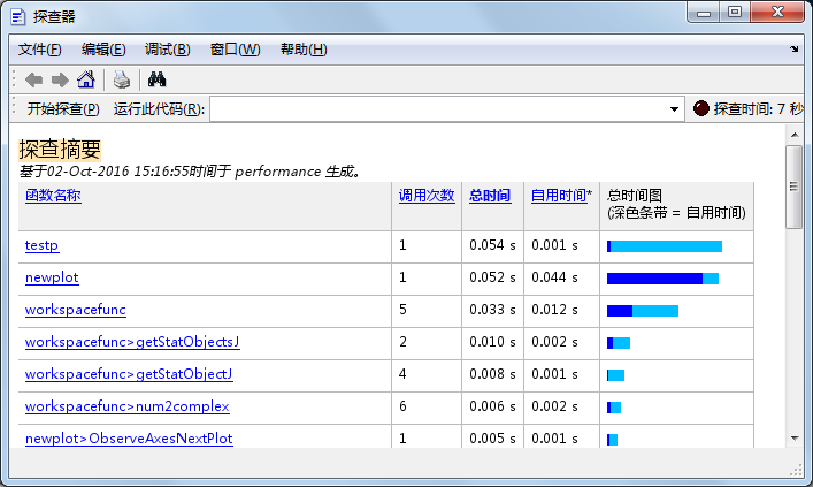
2. 程序优化
（1）采用向量化运算在实际MATLAB程序设计中，为了提高程序的执行速度，常用向量或矩阵运算来代替循环操作。
（2）预分配内存空间 通过在循环之前预分配向量或数组的内存空间可以提高for循环的处理速度。
（3）减小运算强度 在实现有关运算时，尽量采用运算量更小的运算，从而提高运算速度。一般来说，乘法比乘方运算快，加法比乘法运算快。
第5章 MATLAB绘图
5.1 二维图形
5.1.1 绘制二维曲线的基本函数
1. plot函数的基本用法
plot函数的基本调用格式为：
plot(x,y)
其中x和y为长度相同的向量，分别用于存储x坐标和y坐标数据。
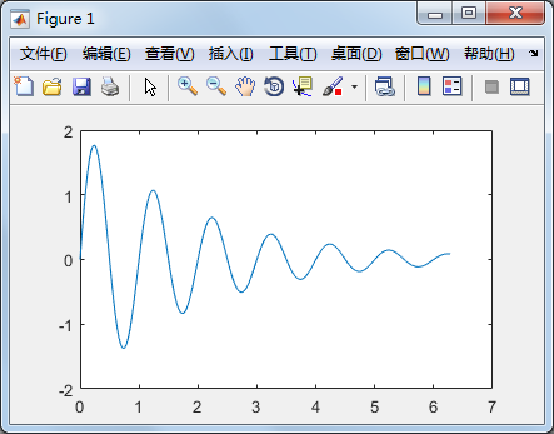
例5-1 在0≤X≤2π区间内，绘制曲线y=2e-0.5xsin(2πx)。
x=0:
pi/100:2*pi;
y=2*exp(-0.5*x).*sin(2*pi*x);
plot(x,y)
例5-2 绘制曲线。 程序如下：
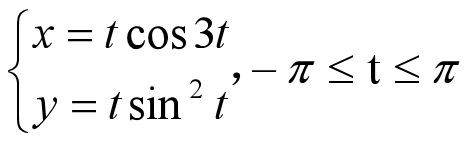
t=-pi:pi/100:pi;
x=t.*cos(3*t);
y=t.*sin(t).*sin(t);
plot(x,y);
说明：
（1）当x是向量，y是矩阵时，x的长度与矩阵y的行数或列数必须相等。如果x的长度等于y的行数，则以x和y的每列为横、纵坐标绘制曲线，曲线的条数等y的列数。如果x的长度等于y的列数，则以x和y的每行为横、纵坐标绘制曲线，曲线的条数等y的行数。
（2）当x、y是同维矩阵时，则以x、y对应列元素为横、纵坐标分别绘制曲线，曲线条数等于矩阵的列数。
（3）plot函数最简单的调用格式是只包含一个输入参数：plot(x)。
2．含多个输入参数的plot函数
含多个输入参数的plot函数调用格式为： plot(x1,y1,x2,y2,…,xn,yn)
3．含选项的plot函数
含选项的plot函数调用格式为： plot(x1,y1,选项1,x2,y2, 选项2,…,xn,yn,选项n)
2．含多个输入参数的plot函数含多个输入参数的plot函数调用格式为： plot(x1,y1,x2,y2,…,xn,yn) 3．含选项的plot函数 含选项的plot函数调用格式为： plot(x1,y1,选项1,x2,y2, 选项2,…,xn,yn,选项n)
|
选项
|
线型
|
选项
|
线型
|
|
-
|
实线（默认值）
|
-.
|
点划线
|
|
:
|
虚线
|
--
|
双划线
|
|
序号
|
选项
|
颜色
|
序号
|
选项
|
颜色
|
|
1
|
b
（
blue
）
|
蓝色
|
5
|
m
（
magenta
）
|
品红色
|
|
2
|
g
（
green
）
|
绿色
|
6
|
y
（
yellow
）
|
黄色
|
|
3
|
r
（
red
）
|
红色
|
7
|
k
（
black
）
|
黑色
|
|
4
|
c
（
cyan
）
|
青色
|
8
|
w
（
white
）
|
白色
|
|
选项
|
标记符号
|
选项
|
标记符号
|
|
.
|
点
|
v
（字母）
|
朝下三角符号
|
|
o
（字母）
|
圆圈
|
^
|
朝上三角符号
|
|
x
（字母）
|
叉号
|
<
|
朝左三角符号
|
|
+
|
加号
|
>
|
朝右三角符号
|
|
*
|
星号
|
p
（
pentagram
）
|
五角星符
|
|
s
（
square
）
|
方块符
|
h
（
hexagram
）
|
六角星符
|
|
d
（
diamond
）
|
菱形符
|
|
|
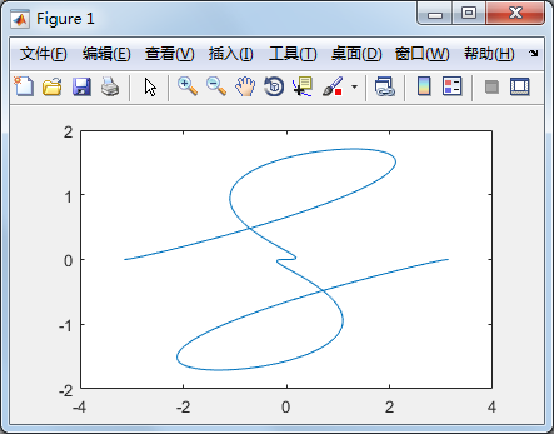
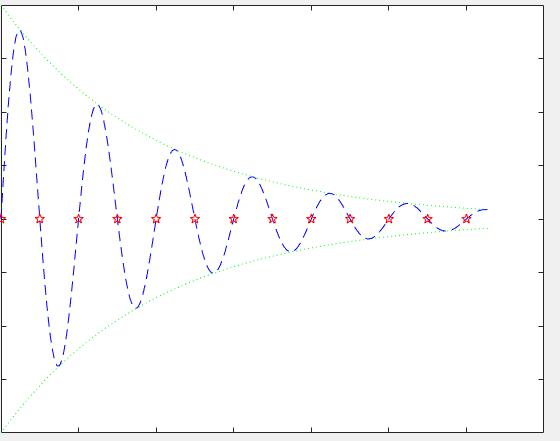
例5-3 用不同线型和颜色在同一坐标内绘制曲线y=2e-0.5xsin(2πx)及其包络线。
程序如下：
x=(0:pi/100:2*pi)';
y1=2*exp(-0.5*x)*[1,-1];
y2=2*exp(-0.5*x).*sin(2*pi*x);
x1=(0:12)/2;
y3=2*exp(-0.5*x1).*sin(2*pi*x1);
plot(x,y1,'g:',x,y2,'b--',x1,y3,'rp');
4．双纵坐标函数plotyy
plotyy函数是MATLAB 5.X新增的函数。
它能把函数值具有不同量纲、不同数量级的两个函数绘制在同一坐标中。
调用格式为：
plotyy(x1,y1,x2,y2)
其中x1-y1对应一条曲线，x2-y2对应另一条曲线。
横坐标的标度相同，纵坐标有两个，左纵坐标用于x1-y1数据对，右纵坐标用于x2-y2数据对。
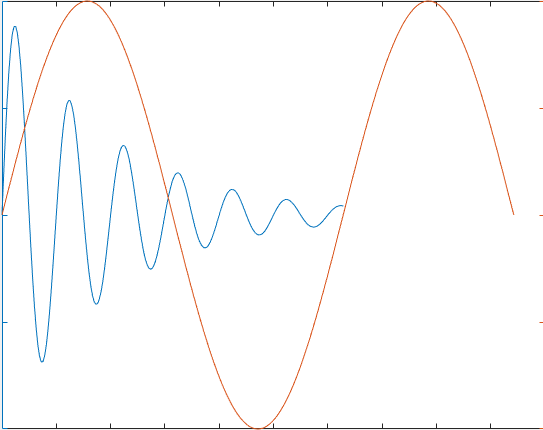
例5-4 用不同标度在同一坐标内绘制曲线y1=e-0.5xsin(2πx)及曲线y2=sin(x)。
程序如下：
x1=0:pi/100:2*pi;
x2=0:pi/100:3*pi;
y1=exp(-0.5*x1).*sin(2*pi*x1);
y2= sin(x2);
plotyy(x1,y1,x2,y2);
5.1.2 绘制图形的辅助操作
1. 图形标注 有关图形标注函数的调用格式为：
title(图形名称)
xlabel(x轴说明)
ylabel(y轴说明)
text(x,y,图形说明)
legend(图例1,图例2,…)
2. 坐标控制
函数的调用格式为：
axis([xmin xmax ymin ymax zmin zmax])
axis函数功能丰富，常用的用法还有：
axis equal 纵、横坐标轴采用等长刻度
axis square 产生正方形坐标系(缺省为矩形)
axis auto 使用缺省设置
axis off 取消坐标轴
axis on 显示坐标轴
grid on/off命令控制是画还是不画网格线，不带参数的grid命令在两种状态之间进行切换。
box on/off命令控制是加还是不加边框线，不带参数的box命令在两种状态之间进行切换。
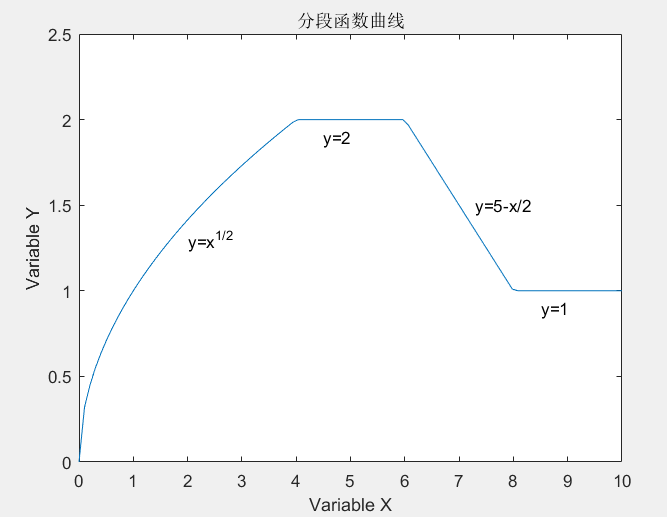
例5-5 绘制分段函数曲线并添加图形标注
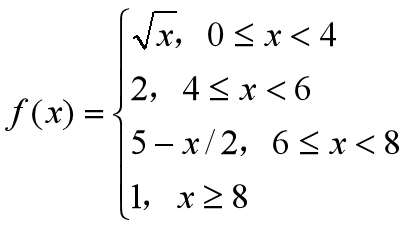
x=linspace(0,10,100);
y=[];
for x0=x
if x0>=8
y=[y,1];
elseif x0>=6
y=[y,5-x0/2];
elseif x0>=4
y=[y,2];
elseif x0>=0
y=[y,sqrt(x0)];
end
end
plot(x,y)
axis([0 10 0 2.5]) %设置坐标轴
title('分段函数曲线'); %加图形标题
xlabel('Variable X'); %加X轴说明
ylabel('Variable Y'); %加Y轴说明
text(2,1.3,'y=x^{1/2}'); %在指定位置添加图形说明
text(4.5,1.9,'y=2');
text(7.3,1.5,'y=5-x/2');
text(8.5,0.9,'y=1');
3. 图形保持
一般情况下，绘图命令每执行一次就刷新当前图形窗口，图形窗口原有图形将不复存在。若希望在已存在的图形上再继续添加新的图形，可使用图形保持命令hold。hold on/off命令控制是保持原有图形还是刷新原有图形，不带参数的hold命令在两种状态之间进行切换。
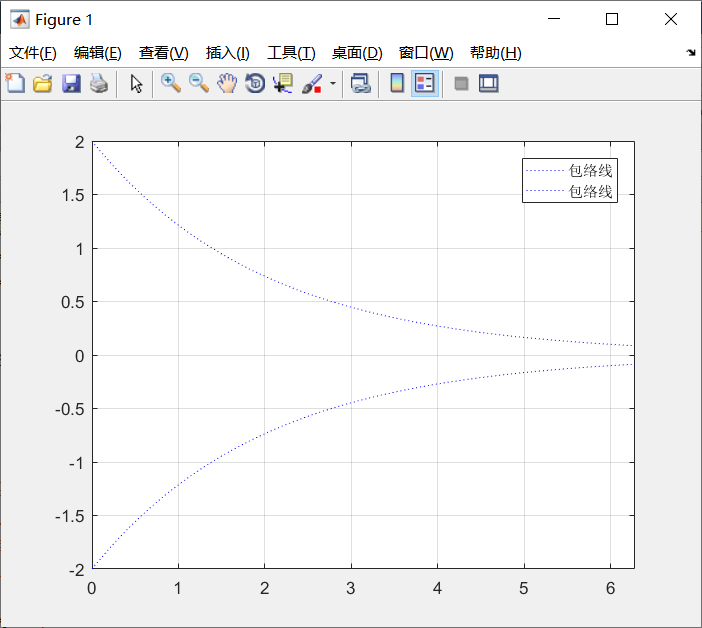
例5-6 用图形保持功能在同一坐标内绘制曲线y=2e-0.5xsin(2πx)及其包络线。
x=(0:pi/100:2*pi)';
y1=2*exp(-0.5*x)*[1,-1];
y2=2*exp(-0.5*x).*sin(2*pi*x);
plot(x,y1,'b:');
axis([0,2*pi,-2,2]); %设置坐标 hold on;
%设置图形保持状态 plot(x,y2,'k');
legend('包络线','包络线','曲线y'); %加图例
hold off; %关闭图形保持
grid %网格线控制
4. 图形窗口的分割
subplot函数的调用格式为： subplot(m,n,p)
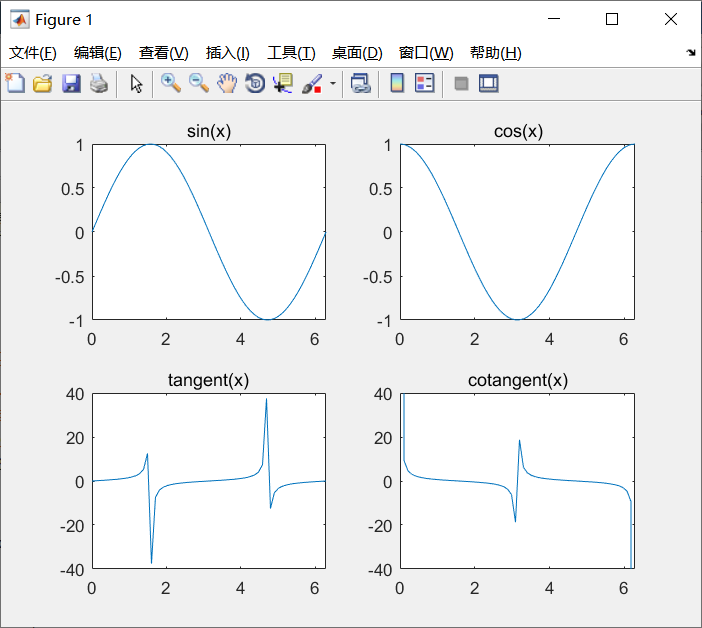
例5-7 在一个图形窗口中以子图形式同时绘制正弦、余弦、正切、余切曲线。
x=linspace(0,2*pi,60);
y=sin(x);z=cos(x);
t=sin(x)./(cos(x)+eps);
ct=cos(x)./(sin(x)+eps);
subplot(2,2,1);
plot(x,y);title('sin(x)');
axis ([0,2*pi,-1,1]);
subplot(2,2,2);
plot(x,z);
title('cos(x)');
axis ([0,2*pi,-1,1]);
subplot(2,2,3);
plot(x,t);
title('tangent(x)');
axis ([0,2*pi,-40,40]);
subplot(2,2,4);
plot(x,ct);
title('cotangent(x)');
axis ([0,2*pi,-40,40]);
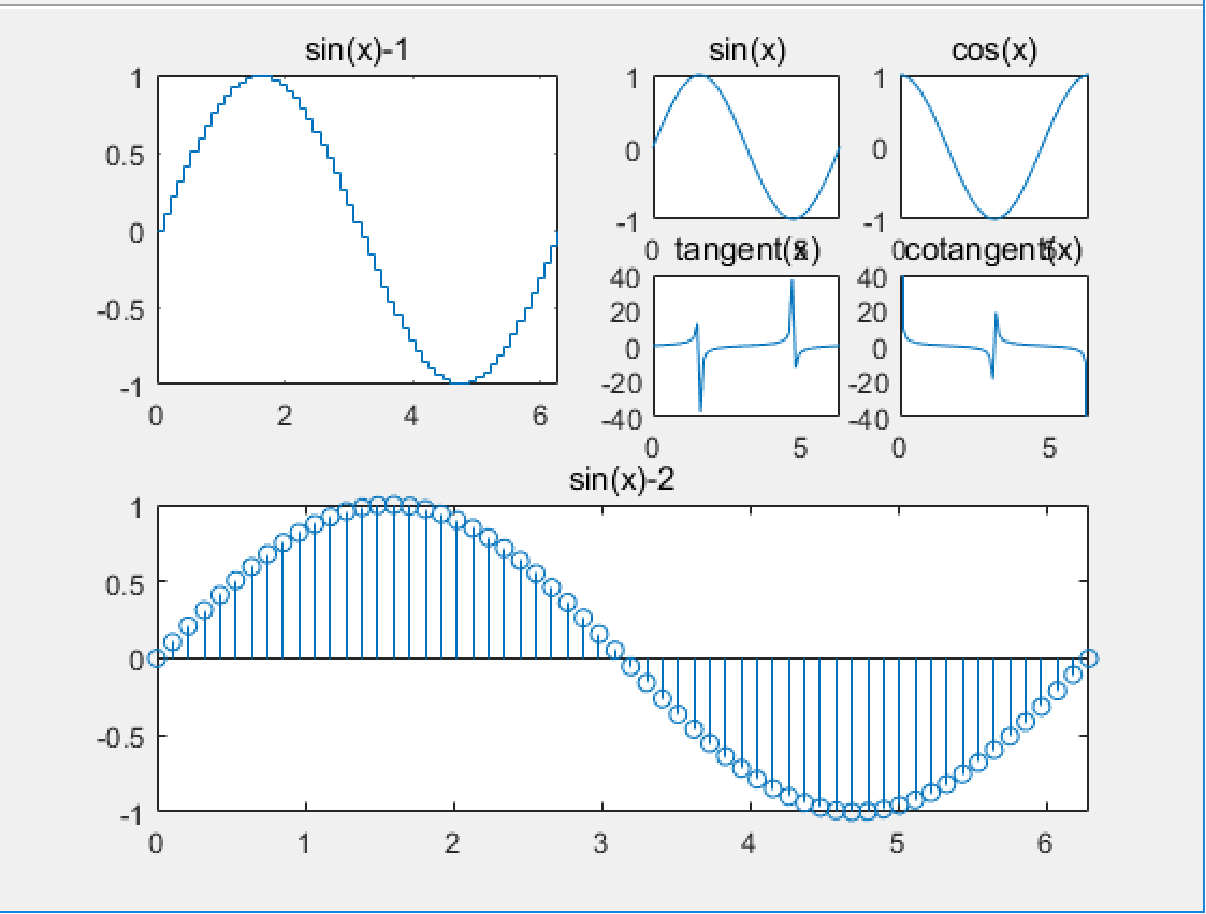
对图形窗口灵活分割。
请看下面的程序。
x=linspace(0,2*pi,60);
y=sin(x);z=cos(x);
t=sin(x)./(cos(x)+eps);
ct=cos(x)./(sin(x)+eps);
subplot(2,2,1); %选择2×2个区中的1号区
stairs(x,y);
title('sin(x)-1');
axis ([0,2*pi,-1,1]);
subplot(2,1,2); %选择2×1个区中的2号区
stem(x,y);
title('sin(x)-2');
axis ([0,2*pi,-1,1]);
subplot(4,4,3); %选择4×4个区中的3号区
plot(x,y);title('sin(x)');
axis ([0,2*pi,-1,1]);
subplot(4,4,4); %选择4×4个区中的4号区
plot(x,z);
title('cos(x)');
axis ([0,2*pi,-1,1]);
subplot(4,4,7); %选择4×4个区中的7号区
plot(x,t);
title('tangent(x)');
axis ([0,2*pi,-40,40]);
subplot(4,4,8); %选择4×4个区中的8号区
plot(x,ct);
title('cotangent(x)');
axis ([0,2*pi,-40,40]);
5.2 其他形式的二维图形
5.2.1 对函数自适应采样的绘图函数
fplot函数的调用格式为：
fplot(fname,lims,tol,选项)
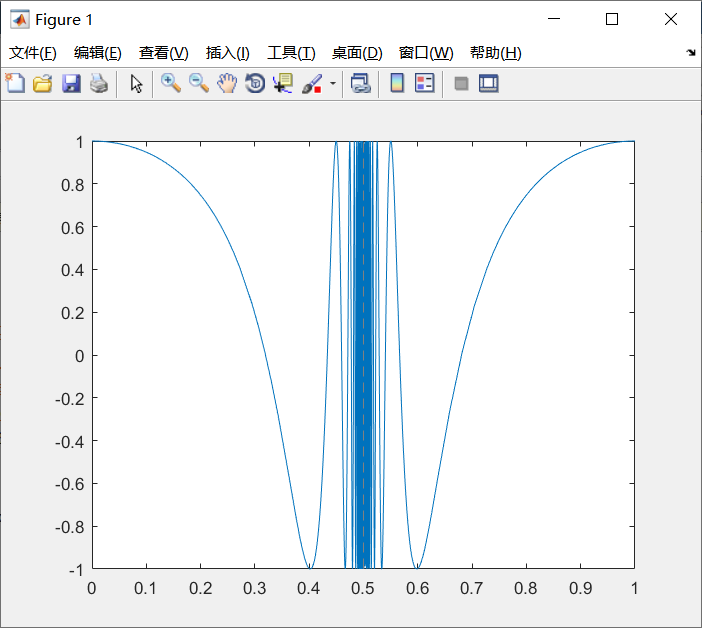
例5-8 用fplot函数绘制f(x)=cos(tan(πx))的曲线。
fplot(@(x)cos(tan(pi*x)),[0,1])
5.2.2 其他坐标系下的二维曲线图
MATLAB提供了绘制对数和半对数坐标曲线的函数
调用格式为：
semilogx(x1,y1,选项1,x2,y2,选项2,…)
semilogy(x1,y1,选项1,x2,y2,选项2,…)
loglog(x1,y1,选项1,x2,y2,选项2,…)
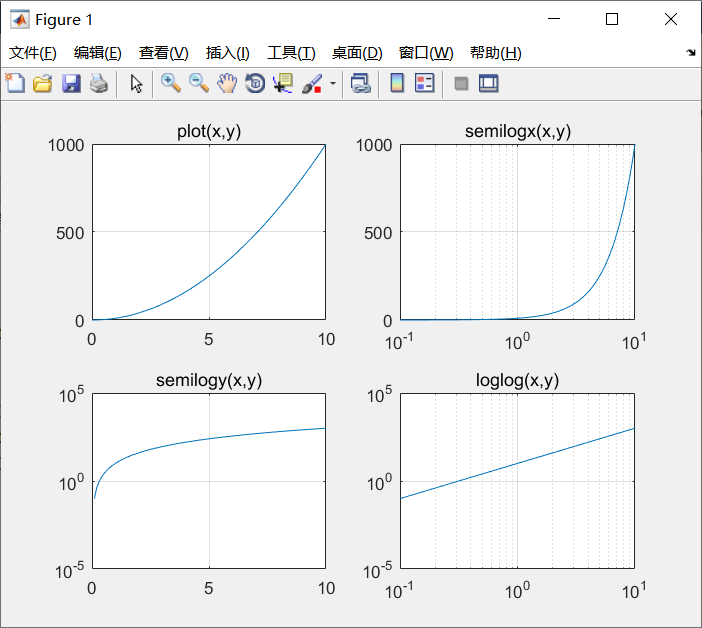
例5-9 绘制y=10x2的对数坐标图并与直角线性坐标图进行比较。
程序如下：
x=0:0.1:10;
y=10*x.*x;
subplot(2,2,1);
plot(x,y);
title('plot(x,y)');
grid on;
subplot(2,2,2);
semilogx(x,y);
title('semilogx(x,y)');
grid on;
subplot(2,2,3);
semilogy(x,y);
title('semilogy(x,y)');
grid on;
subplot(2,2,4);
loglog(x,y);
title('loglog(x,y)');
grid on;
2．极坐标图polar函数用来绘制极坐标图，其调用格式为：
polar(theta,rho,LineSpec)
其中theta为极坐标极角，rho为极坐标矢径，选项的内容与plot函数相似。
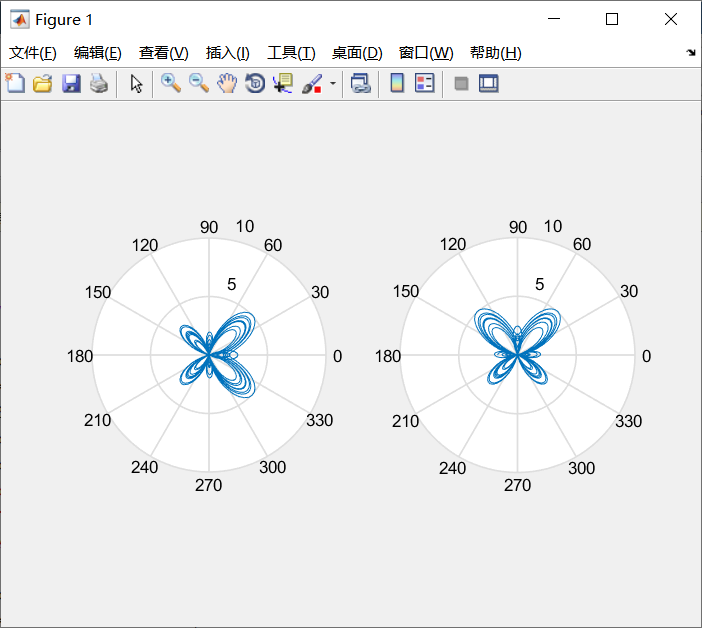
例5-10 绘制极坐标图。
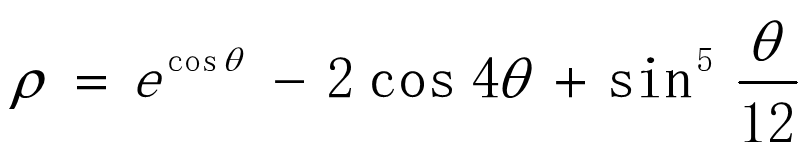
t=0:pi/50:20*pi;
r1=exp(cos(t))-2*cos(4*t)+sin(t/12).^5;
r2=exp(cos(t-pi/2))-2*cos(4*(t-pi/2))+sin((t-pi/2)/12).^5;
subplot(1,2,1)
polar(t,r1) %绘制蝴蝶曲线
subplot(1,2,2)
polar(t,r2) %旋转90度的蝴蝶曲线
5.2.3 其他特殊二维图形
1. 其他形式的线性直角坐标图
在线性直角坐标系中，其他形式的图形有条形图、阶梯图、杆图和填充图等
(1) 条形类图形 bar(y) bar(x,y,选项)
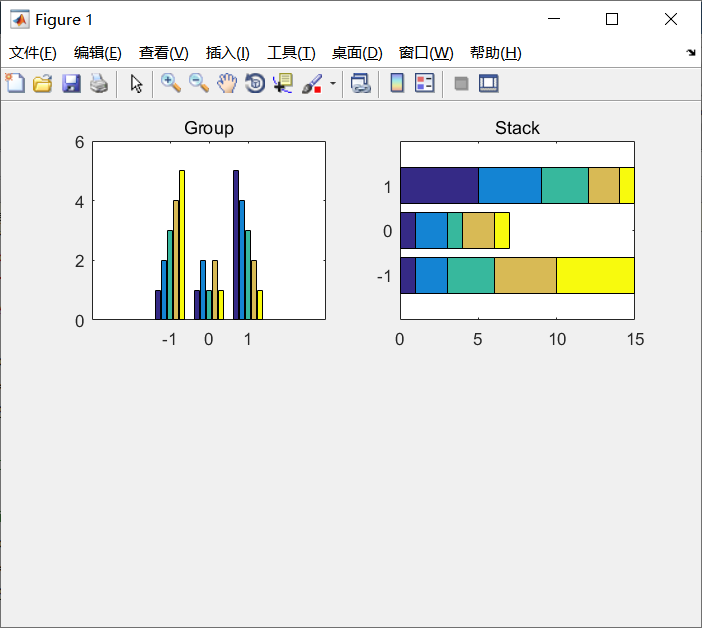
例5-11 条形图应用示例。
程序如下：
x=-1:1;
y=[1,2,3,4,5;1,2,1,2,1;5,4,3,2,1];
subplot(2,2,1);
bar(x,y,'grouped')
title('Group');
axis([-3,3,0,6])
subplot(2,2,2);
barh(x,y,'stacked')
title('Stack')
（2）直方图在MATLAB中，绘制直方图的函数有两个：
hist函数和rose函数，分别用于绘制直角坐标系下的直方图和极坐标系下的直方图，后者也称为玫瑰花图。
hist函数的应用更为广泛一些，其调用格式为： hist(y[,x])
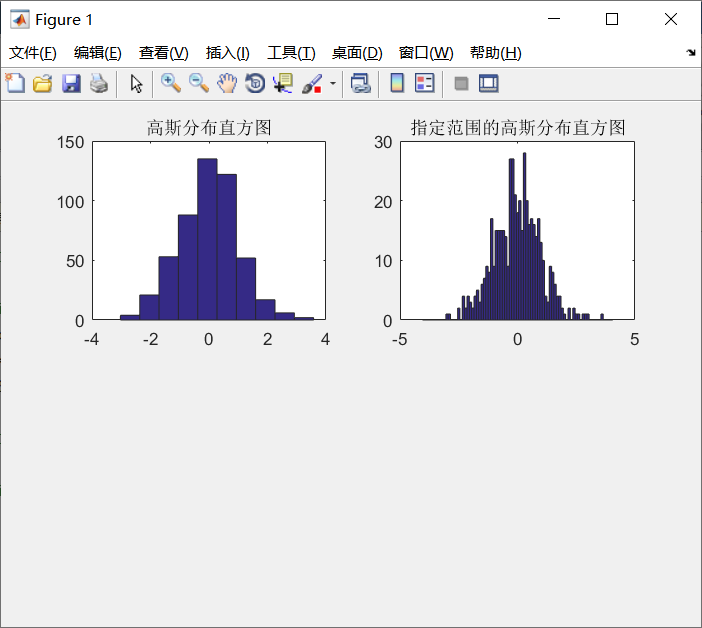
例5-12 绘制服从高斯分布的直方图，再将这些数据分到指定范围的区间中，并绘制直方图中。
y=randn(500,1);
subplot(2,2,1)
hist(y);
title('高斯分布直方图')
x=-4:0.1:4;
subplot(2,2,2)
hist(y,x);
title('指定范围的高斯分布直方图')
rose函数的调用格式与hist函数非常相似，调用方法如下：
rose(theta[,x])
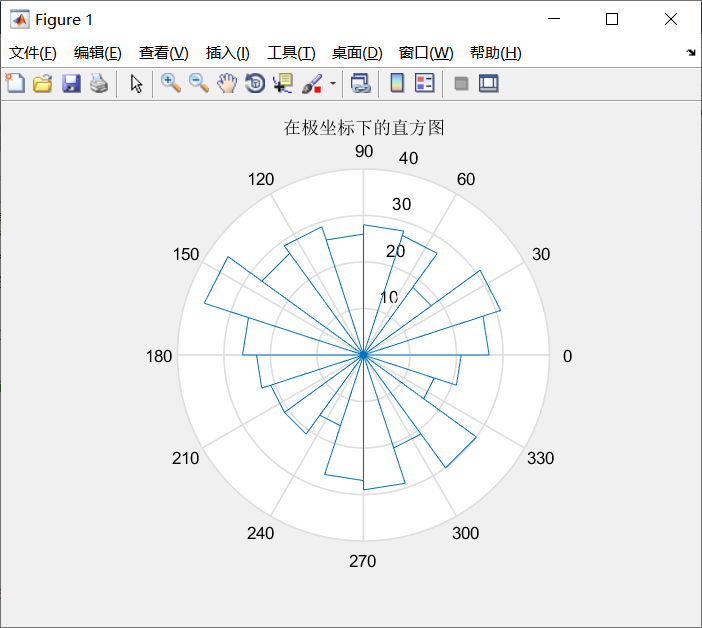
例5-13 绘制例5-12中高斯分布数据在极坐标下的直方图。
y=randn(500,1);
theta=y*pi;
rose(theta)
title('在极坐标下的直方图')
2．面积类图形
（1）扇形统计图 扇形统计图又称为饼图，反映一个数据系列中各个分量在总数量中所占的比重。
MATLAB提供了pie函数来绘制扇形统计图，其调用格式为： pie(x,explode)
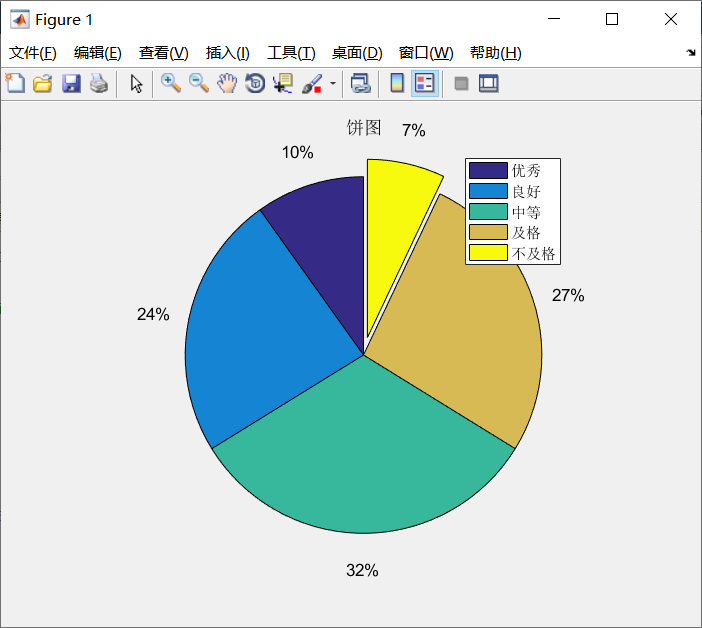
例5-14 某次考试优秀、良好、中等、及格、不及格的人数分别为：7、17、23、19、5，试用扇形统计图作成绩统计分析。
程序如下：
pie([7,17,23,19,5],[0,0,0,0,1]) %对应第5分量部分从饼图中心分离
title('饼图')
legend('优秀','良好','中等','及格','不及格')
（2）面积统计图
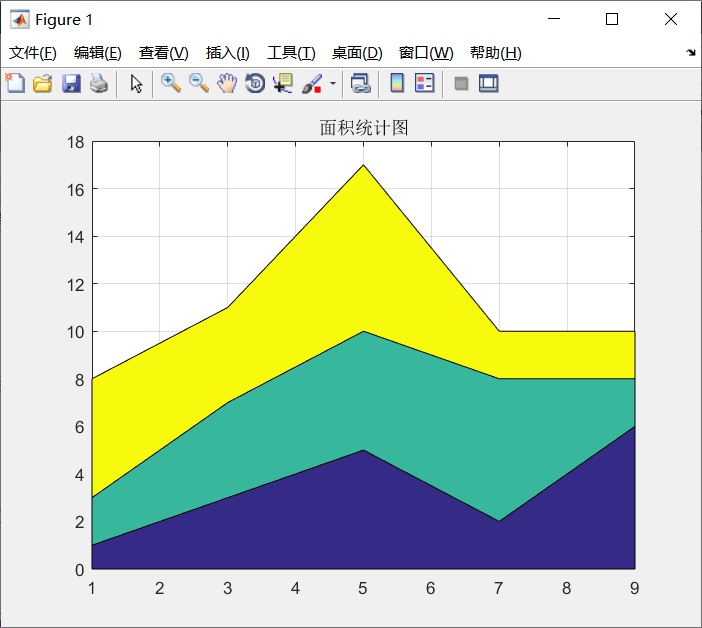
面积统计图反映数量变化的趋势，在实际中可以表现不同部分对整体的影响。
在MATLAB中，绘制面积统计图的函数是area，其调用格式为： ① area(x)。 ② area(x,y)
x=1:2:9;
y=[1,3,5,2,6;2,4,5,6,2;5,4,7,2,2]';
area(x,y);
gridon;
title('面积统计图')
（3）实心图实心图是将数据的起点和终点连成多边形，并填充颜色。
绘制实心图的函数是fill，其调用格式为： fill(x,y,颜色)
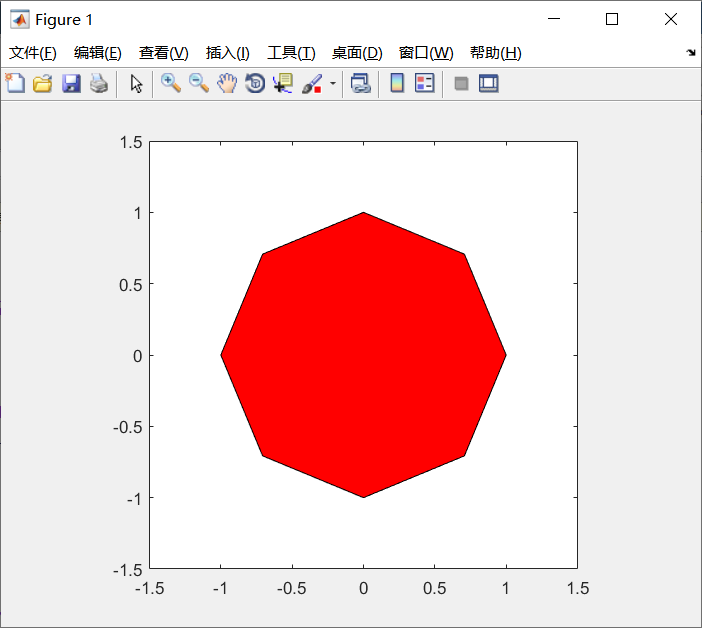
例5-15 绘制一个红色的正八边形。
t=0:2*pi/8:2*pi; %取正八边形坐标点 t=[t,t(1)]; %数据向量的首尾重合，使图形封闭。
x=sin(t);
y=cos(t);
fill(x,y,'r') %x、y是圆周坐标，数据间隔足够小时可以画圆
axis equal;
axis([-1.5,1.5,-1.5,1.5])
3．散点类图形
MATLAB提供了绘制散点类图形的函数scatter、stairs和stem，分别用于绘制散点图、阶梯图和杆图。
3个函数的调用格式为： scatter(x,y[,'filled'][,颜色]) stairs(x,y,选项) stem(x,y,选项)
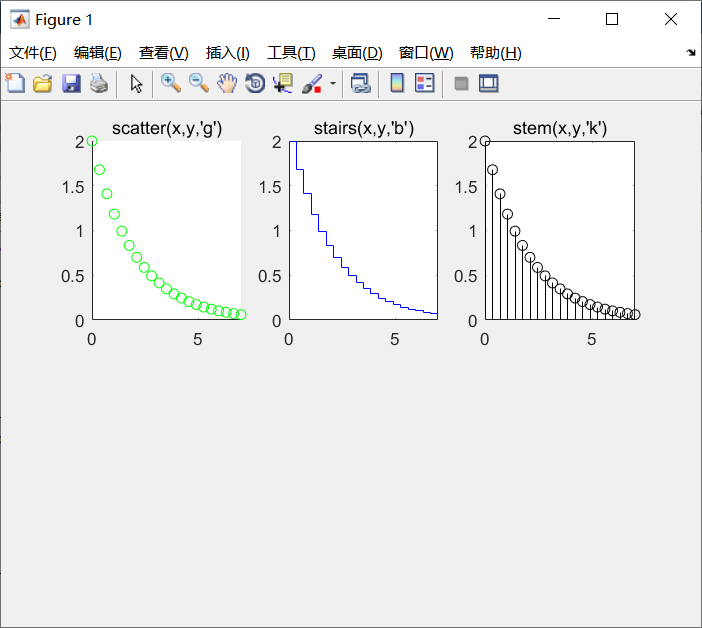
例5-16 分别以散点图、阶梯图和杆图形式绘制曲线y=2e-0.5x。
程序如下：
x=0:0.35:7;
y=2*exp(-0.5*x);
subplot(2,3,1);
scatter(x,y,'g');
title('scatter(x,y,''g'')');
axis([0,7,0,2])
subplot(2,3,2);
stairs(x,y,'b') ;
title('stairs(x,y,''b'')');
axis([0,7,0,2])
subplot(2,3,3);
stem(x,y,'k') ;
title('stem(x,y,''k'')');
axis([0,7,0,2])
4．矢量类图形
（1）罗盘图
罗盘图表示起点为坐标原点的向量，同时还在坐标系中显示圆形的分隔线。
① compass(x,y) 。
② compass(z)
（2）羽毛图
① feather(x,y) 。
② feather(z) 。
（3）箭头图
quiver([x,y,]u,v)
例5-17 分别以罗盘图、羽毛图和箭头图形式绘制绘制正弦曲线。
x=-pi:pi/8:pi;
y=sin(x);
subplot(2,2,1);
compass(x,y)
title('罗盘图')
subplot(2,2,2);
feather(x,y)
title('羽毛图')
subplot(2,1,2);
quiver(x,y)
title('箭头图')
最后
以上就是魁梧战斗机为你收集整理的MATLAB总结的全部内容，希望文章能够帮你解决MATLAB总结所遇到的程序开发问题。
如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。
本图文内容来源于网友提供，作为学习参考使用，或来自网络收集整理，版权属于原作者所有。
发表评论 取消回复