1. 首页
  2. 文章中心
  3. Control

Apollo代码解析Lateral Control：横向控制算法与流程图（基于动力学模型的LQR）LQR算法的输入：LQR算法的输出：LQR算法的计算过程：LQR横向控制算法主要有3个关键模块:优化提高篇：预测模块，考虑控制的延时以及车辆的惯性，可提高横向控制的精度以下以匀速直线运动为例，列举预测模块的预测模型：

177 阅读 0 评论
我是靠谱客的博主 动人花瓣，这篇文章主要介绍Apollo代码解析Lateral Control：横向控制算法与流程图（基于动力学模型的LQR）LQR算法的输入：LQR算法的输出：LQR算法的计算过程：LQR横向控制算法主要有3个关键模块:优化提高篇：预测模块，考虑控制的延时以及车辆的惯性，可提高横向控制的精度以下以匀速直线运动为例，列举预测模块的预测模型：，现在分享给大家，希望可以做个参考。

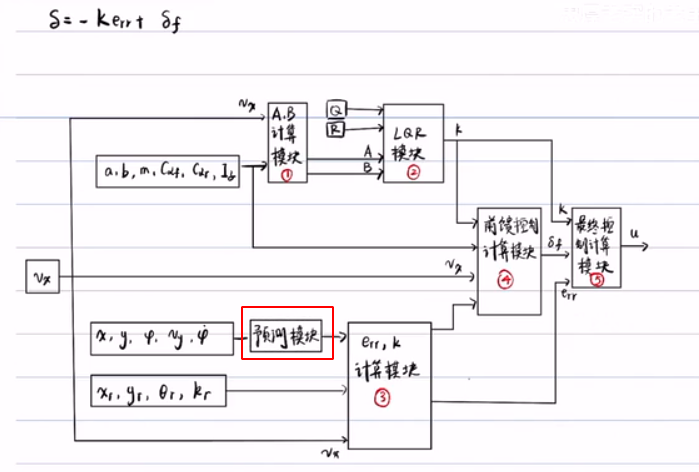
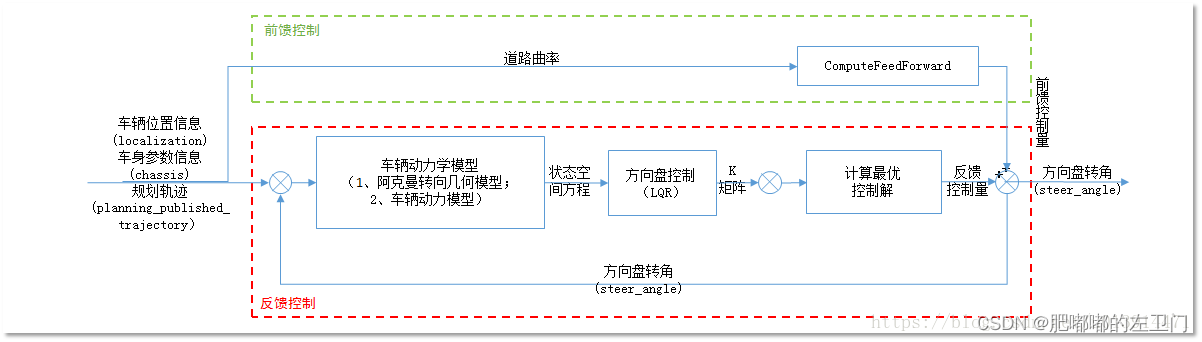
在这里插入图片描述
在这里插入图片描述

基于动力学模型的LQR前提假设：

1，小角度转向，故规划路径的曲率不能变化过快；
2，认为车速恒定，故加速度不能过大或过小，加速度尽可能小；

LQR算法的输入：

1，整车参数：用于求解LQR模块所需的A,B矩阵

2，车辆实时状态参数：速度，质心坐标，航向角，方向盘转角

3，规划的离散轨迹点参数：坐标，航向角，曲率

LQR算法的输出：

在这里插入图片描述

LQR算法的计算过程：

在这里插入图片描述

*注：其中的曲率k不一定是投影点曲率，而是目标点曲率，

目标点可能有3种情况：1，最近点；2，投影点；3，根据前视距离所确定的目标点。*

LQR横向控制算法主要有3个关键模块:

1，LQR模块：求解反馈矩阵K;

2，横向误差计算模块：求解误差的状态变量Error;

3，前馈模块：补偿道路曲率对稳态误差的影响，消除稳态误差。

则最终的方向盘转角为：

在这里插入图片描述

一、 LQR模块:求解反馈矩阵K

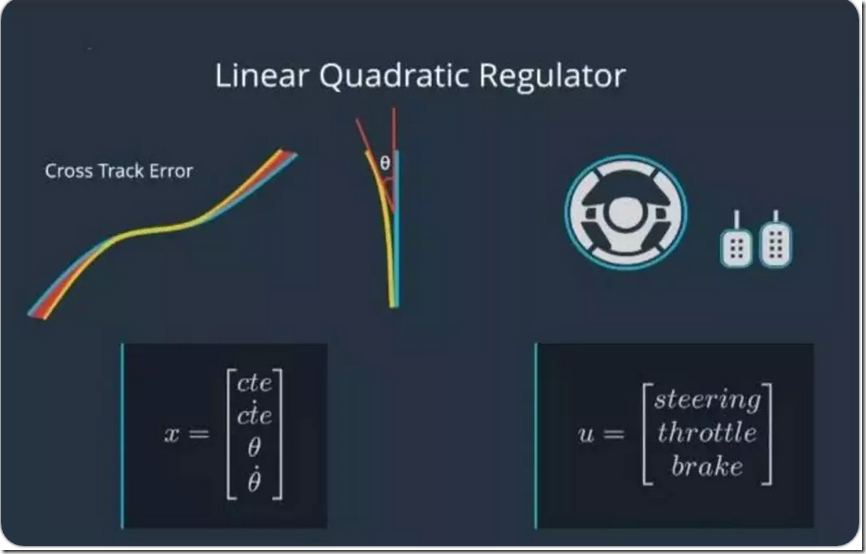
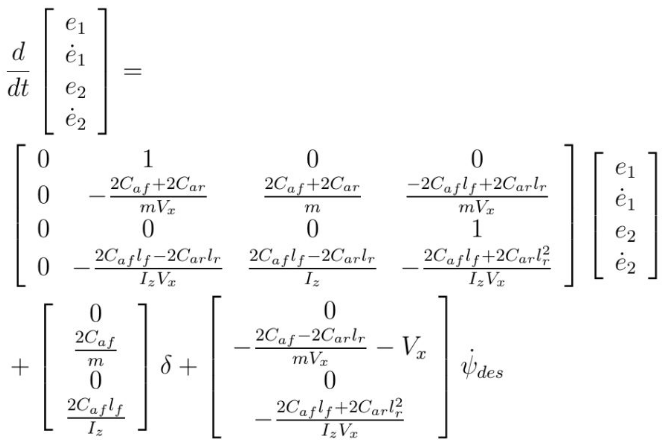
在这里插入图片描述

车辆动力学模型状态方程：
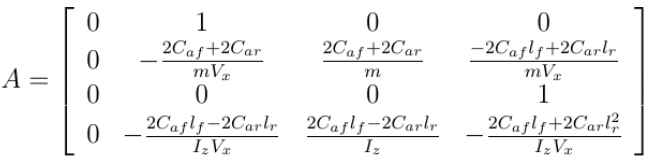
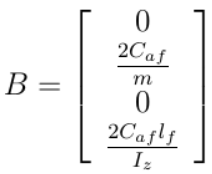
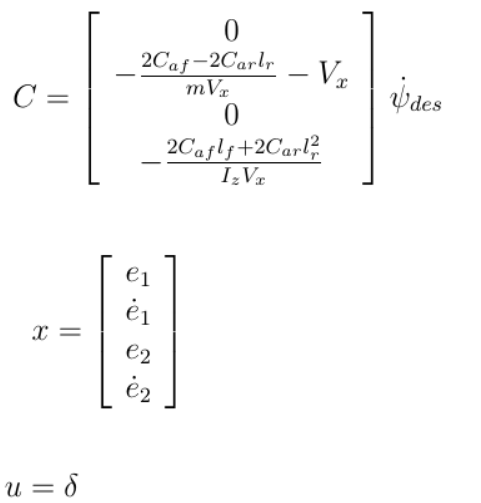
在这里插入图片描述
令：
在这里插入图片描述在这里插入图片描述
在这里插入图片描述
则可得到状态方程为：
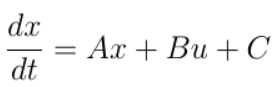
在这里插入图片描述

但因为需要使用计算机进行数值计算，推导截至到上面的连续模型还不够，还需要对上述模型进行近似离散化,近似离散化后的模型为：

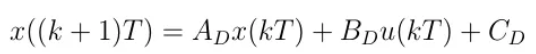
在这里插入图片描述
其中：
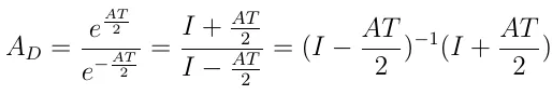
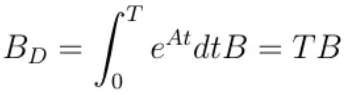
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述在这里插入图片描述
故，在工程中，LQR算法的求解过程可以总结为4步：
1，令P等于状态权重矩阵;
2，迭代黎卡提方程求出新的P;
3，当两次P的差值足够小时，计算反馈矩阵K;,
4，根据反馈矩阵K获取最优控制量u；

复制代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
bool LQRSolver(const Eigen::MatrixXd &AD, const Eigen::MatrixXd &BD,
                     const Eigen::MatrixXd &Q, const Eigen::MatrixXd &R,
                     const double tolerance,
                     const unsigned int max_num_iteration,
                     Eigen::MatrixXd &ptr_K, unsigned int &out_iteration_num,
                     double &out_err) {
  Eigen::MatrixXd P = Q;  // init P=S=Q P(k)
  std::ostringstream ss;
  ss << "G Matrix" << AD << std::endl;
  ss << "H Matrix" << BD << std::endl;
  ss << "Q Matrix" << Q << std::endl;
  ss << "R Matrix" << R << std::endl;
  // NM_DEBUG(ss.str());
  Eigen::MatrixXd AD_T = AD.transpose();
  Eigen::MatrixXd BD_T = BD.transpose();
  unsigned int iteration_num = 0;
  double err = std::numeric_limits<double>::max();
  clock_t t;
  t = clock();
  NM_DEBUG("lqr--before solve");
  while (err > tolerance && iteration_num < max_num_iteration) {
    iteration_num++;
    Eigen::MatrixXd P_MO =
        Q +
        AD_T * P * (AD - BD * (R + BD_T * P * BD).inverse() * BD_T * P * AD);
    err = fabs((P_MO - P).maxCoeff());
    P = P_MO;
  }
  NM_DEBUG("lqr--end solve {}", iteration_num);
  out_iteration_num = iteration_num;
  out_err = err;
  if (iteration_num >= max_num_iteration) {
    NM_ERROR("Over iterate ERR= {}", err);
    t = clock() - t;
    NM_DEBUG_STREAM("It took me " << (static_cast<double>(t) / CLOCKS_PER_SEC)
                                  << " seconds");
    return false;

  } else {
    ptr_K = (R + BD.transpose() * P * BD).inverse() * BD.transpose() * P * AD;
    return true;
  }
}

二，横向误差计算模块：求解误差状态变量Error;

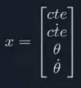
在这里插入图片描述
4个元素分别为：
1，横向位置误差lateral_error（重点及难点）；
2，横向位置误差变化率lateral_error_rate；
3，航向误差heading_error；
3，航向误差变化率heading_error_rate；

1,横向位置偏差的求解方法解析（重点即难点）

基础知识：二维坐标系转换

在坐标系XOY下点P的坐标为(x,y)，将XOY坐标系逆时针旋转θ角度后得到新坐标系X* O Y*,则点P在新坐标系下的坐标为：
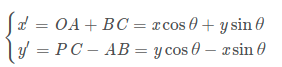
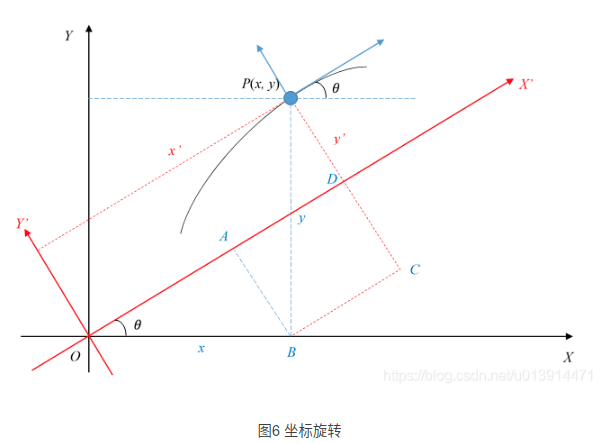
在这里插入图片描述
在这里插入图片描述
横纵向位置偏差跟期望目标点的方向有关，故工程应用中均是在Frenet坐标系下求取横纵向位置偏差的值，故涉及笛卡尔坐标系与Frenet坐标的转换
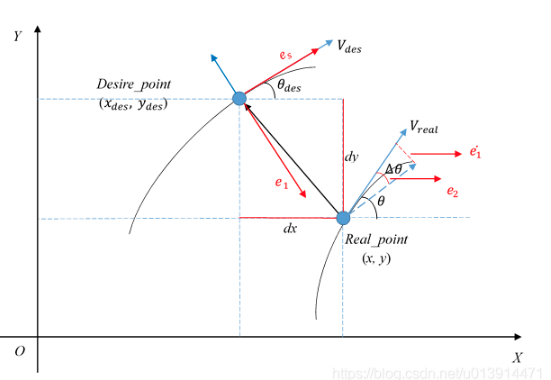
在这里插入图片描述
首先，在笛卡尔坐标系中，参考点与真实点间在X、Y轴方向的误差：
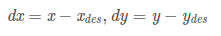
在这里插入图片描述
由上述二维坐标转换的公式可知：
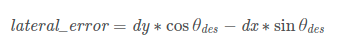
在这里插入图片描述

代码如下，横纵向误差求解代码表述有异，但殊途同归：

复制代码
1
2
3
4
5
6
7
8
  // 横向控制
  const double dx = x - target_point.path_point().x();
  const double dy = y - target_point.path_point().y();
  
  const double cos_target_heading = std::cos(target_point.path_point().theta());
  const double sin_target_heading = std::sin(target_point.path_point().theta());
  double lateral_error = cos_target_heading * dy - sin_target_heading * dx;

2,横向位置偏差变化率，航向角偏差，航向角偏差变化率的求解方法解析

航向角偏差 = 车辆实际航向角 - 目标点航向角；
横向位置偏差变化率 = 线速度 × sin(航向角偏差);
航向角偏差变化率 = 车辆实际角速度 - 目标点角速度。

复制代码
1
2
3
4
5
6
7
8
  double heading_error =
      common::angles::normalize_angle(theta - model_state.reference_yaw);
  double lateral_error_dot = linear_v * std::sin(heading_error);
  double target_heading_rate =
      target_waypoint.curvature() * target_waypoint.velocity();
  double heading_error_rate =  angular_v - target_heading_rate;

至此状态变量X得以求解。

三、前馈模块：根据公式求解即可

当车辆在曲线道路上行驶时，并不能完全消除跟踪误差，因此引入和道路曲率相关的前馈控制器以帮助消除跟踪误差，输入量只有一个曲率，计算公式如下（公式出处：Vehicle Dynamics and Control 第3章，该章节对方向盘控制做了详解）：
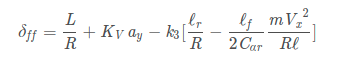
在这里插入图片描述
其中， K_V为不足转向梯度，表征了车辆的转向特性
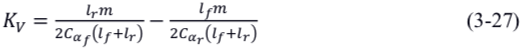
在这里插入图片描述
代码如下：

复制代码
1
2
3
4
5
6
7
8
const double kv =
      lr_ * mass_ / 2 / cf_ / wheelbase_ - lf_ * mass_ / 2 / cr_ / wheelbase_;
const double steer_angle_feedforward =
      (wheelbase_ * ref_curvature + kv * v * v * ref_curvature -
       matrix_k_(0, 2) *
           (lr_ * ref_curvature -
            lf_  / (2*cr_) - mass_ * v * v * ref_curvature / wheelbase_));

四、至此，根据如下公式算出最终的方向盘转角：

在这里插入图片描述

优化提高篇：预测模块，考虑控制的延时以及车辆的惯性，可提高横向控制的精度

根据车辆实时方向盘角度的大小不同，预测的处理方式不同：

1，当方向盘角度较小时，可以近似认为预测时段内车辆是匀速直线运动，一般是中高速城市场景下

2，当方向盘角度较大时，可以近似认为预测时段内车辆是匀速圆弧运动，一般是低速泊车场景

以下以匀速直线运动为例，列举预测模块的预测模型：

在这里插入图片描述

在这里插入图片描述

最后

以上就是动人花瓣最近收集整理的关于Apollo代码解析Lateral Control：横向控制算法与流程图（基于动力学模型的LQR）LQR算法的输入：LQR算法的输出：LQR算法的计算过程：LQR横向控制算法主要有3个关键模块:优化提高篇：预测模块，考虑控制的延时以及车辆的惯性，可提高横向控制的精度以下以匀速直线运动为例，列举预测模块的预测模型：的全部内容，更多相关Apollo代码解析Lateral内容请搜索靠谱客的其他文章。

本图文内容来源于网友提供，作为学习参考使用，或来自网络收集整理，版权属于原作者所有。
点赞(117)

相关文章

Arduino机器人：跟随我 - 线跟随 - 相扑 - 绘图 - 避障
Arduino机器人：跟随我 - 线跟随 - 相扑 - 绘图 - 避障
树莓派视觉小车 -- 小球追踪（颜色追踪）（OpenCV色彩空间HSV）效果展示 基础理论（HSV）一、初始化二、运动函数三、舵机控制四、在HSV空间下获取二值图五、图像处理（总）六、运动控制总代码
树莓派视觉小车 -- 小球追踪（颜色追踪）（OpenCV色彩空间HSV）效果展示 基础理论（HSV）一、初始化二、运动函数三、舵机控制四、在HSV空间下获取二值图五、图像处理（总）六、运动控制总代码
嵌入式软件开发—回顾及总结
嵌入式软件开发—回顾及总结
硬件电路设计纯纯小白-1-单片机晶振
硬件电路设计纯纯小白-1-单片机晶振
Apollo代码解析Lateral Control：横向控制算法与流程图（基于动力学模型的LQR）LQR算法的输入：LQR算法的输出：LQR算法的计算过程：LQR横向控制算法主要有3个关键模块:优化提高篇：预测模块，考虑控制的延时以及车辆的惯性，可提高横向控制的精度以下以匀速直线运动为例，列举预测模块的预测模型：
Apollo代码解析Lateral Control：横向控制算法与流程图（基于动力学模型的LQR）LQR算法的输入：LQR算法的输出：LQR算法的计算过程：LQR横向控制算法主要有3个关键模块:优化提高篇：预测模块，考虑控制的延时以及车辆的惯性，可提高横向控制的精度以下以匀速直线运动为例，列举预测模块的预测模型：
控制算法总结控制算法
控制算法总结控制算法
经典算法的流程
经典算法的流程
四轮 控制算法 麦轮_四轮麦克纳姆轮巡检机器人运动控制方法与流程
四轮 控制算法 麦轮_四轮麦克纳姆轮巡检机器人运动控制方法与流程

评论列表共有 0 条评论

立即
投稿
返回
顶部