什么是取整？有几种取整方式？C语言又是哪种方式？取模取余一样吗？

80 阅读 0 评论 53 点赞

我是靠谱客的博主成就毛巾，最近开发中收集的这篇文章主要介绍什么是取整？有几种取整方式？C语言又是哪种方式？取模取余一样吗？，觉得挺不错的，现在分享给大家，希望可以做个参考。

概述

大家都知道取整这回事，但是对于取整只有单一的认识，请看下面代码。

int main()
{
	int j = -2.9;
	int i = 2.9;
	printf("%dn", j);
	printf("%dn", i);
	return 0;
}

看这串代码我们先不管数据溢出的问题，直接看最后的结果等于什么

大家都知道最后结果会是-2.9变成-2，2.9变成2.

但是为什么会这样呢？我相信比较多人是不知道的

是因为一共有四种取整方式

第一种取整模式：向0取整

我们C语言默认是向0取整所以才等于这个结果

向0取整的意思是：只要你不是整数就把余数抹掉，变成整数。不是我们理解的四舍五入。

C语言里面有一个函数是和向0取整是一样作用，trunc函数。看代码

#define _CRT_SECURE_NO_WARNINGS
#include<stdio.h>
#include<math.h>//使用trunc这个函数要调用这个库函数

int main()
{
	int j = -2.9;
	int i = 2.9;
	printf("%dn", (int)trunc(j));//因为trunc这个函数返回的是浮点数，所以要强转成int
	printf("%dn", (int)trunc(i));
	return 0;
}

如图所示，是一摸一样的。

第二种取整模式：负无穷取整，floor取整

负无穷取整的意思是：只要是负数有余数就进一位，正数和向0取整一样

代码验证

#define _CRT_SECURE_NO_WARNINGS
#include<stdio.h>
#include<math.h>//使用trunc这个函数要调用这个库函数

int main()
{
	printf("%lfn",floor(-2.1));
	printf("%lfn",floor(-2.9));
	printf("%lfn", floor(2.1));
	printf("%lfn", floor(2.9));
	return 0;
}

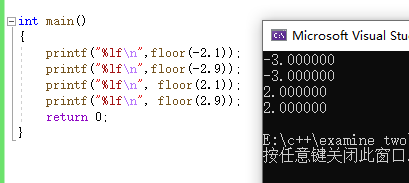
因为是负无穷取整-2.1和-2.9变成-3.0，正数2.1和2.9是向0取整的原则变成了2.0

第三种取整方式：向正无穷取整，ceil取整

正无穷取整模式：正数只要有余数就进1，负数和向0取整

代码验证

#define _CRT_SECURE_NO_WARNINGS
#include<stdio.h>
#include<math.h>//使用trunc这个函数要调用这个库函数

int main()
{
	printf("%lfn",ceil(-2.1));
	printf("%lfn",ceil(-2.9));
	printf("%lfn",ceil(2.1));
	printf("%lfn",ceil(2.9));
	return 0;
}

因为是正无穷取整2.1和2.9都有余数所以进1变成了3.0，-2.1和-2.9 一样是向0取整的原则等于2.0

第四种取整方式：四舍五入取整，round取整

四舍五入模式：就是我们数学进位用的那个

代码验证

#define _CRT_SECURE_NO_WARNINGS
#include<stdio.h>
#include<math.h>//使用trunc这个函数要调用这个库函数

int main()
{
	printf("%lfn",round(-2.1));
	printf("%lfn",round(-2.9));
	printf("%lfn",round(2.1));
	printf("%lfn",round(2.9));
	return 0;
}

四舍五入-2.1余数不是四以上所以等于-2.0，-2.9余数大于4所以进1等于-3.0，2.1和-2.1一样，2.9和-2.9一样

四种取整方式的汇总代码

#define _CRT_SECURE_NO_WARNINGS
#include<stdio.h>
#include<math.h>//使用trunc这个函数要调用这个库函数

int main()
{
	const char* format = "%.1f t%.1f t%.1f t%.1f t%.1fn";
	printf("valuetroundtfloortceilttruncn");
	printf("-----t-----t-----t----t-----n");
	printf(format, 2.3, round(2.3), floor(2.3), ceil(2.3), trunc(2.3));
	printf(format, 3.8, round(3.8), floor(3.8), ceil(3.8), trunc(3.8));
	printf(format, 5.5, round(5.5), floor(5.5), ceil(5.5), trunc(5.5));
	printf(format, -2.3, round(-2.3), floor(-2.3), ceil(-2.3), trunc(-2.3));
	printf(format, -3.8, round(-3.8), floor(-3.8), ceil(-3.8), trunc(-3.8));
	printf(format, -5.5, round(-5.5), floor(-5.5), ceil(-5.5), trunc(-5.5));
	return 0;
}

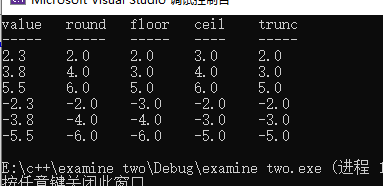
我们从图可以看见，有的取整方式不同但是最后取整结果有的是相同的

大家在这里可能就会想了，为什么要有那么多种取整方式。难道是和大小端一样？吃鸡蛋先吃大头还是小头一样？

其结果其实是各有各的用处，比如负无穷取整，像女孩子都希望自己年龄小点，女孩子实在要回答年龄的话，17岁9个月，都会回答成17岁。

像正无穷取整，有的年轻人有本事坐上了领导这个位置，怕年龄小，服不了底下员工，所以会把年龄取大点。

这些东西就不多聊了

我们来聊聊取模

为什么这里会等于1呢？难道是10/3剩余1，所以等于1吗？

不对哦！！！取模和取余是有区别的哦

我们用取模简单公式来分析下结果

取模的基本概念

如果a和d是两个自然数，d非零，可以证明存在两个唯一的整数 q 和 r，满足 a = q*d + r 且0 ≤ r < d。其中，q 被称为商，r 被称为余数。

我们来带入一下公式，我们来求10%3的模

因为：a=10,d=3,q=3,r=1 0<=r<d(3)
所以：a = q*d+r -> 10=3*3+1

如果是这样呢？

那要是换成python呢？

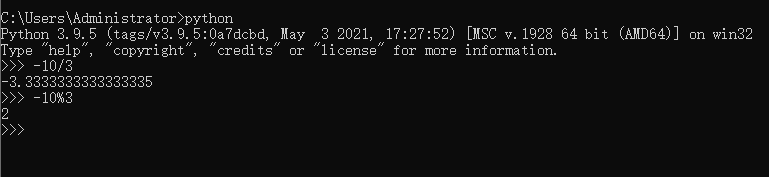
可以看到3.9.5版本的python出来的答案和C语言的答案是不一样的

结论：可以看到单单是知道取模的基本定义是不够用的

因为在C中，现在 - 10 % 3出现了负数，根据定义：满足 a = q * d + r 且0 ≤ r < d，C语言中的余数，是不满足定义的，
   因为，r < 0了。
   故，大家对取模有了一个修订版的定义：
   如果a和d是两个自然数，d非零，可以证明存在两个唯一的整数 q 和 r，满足 a = q * d + r, q 为整数，且0 ≤ | r |
   < | d | 。其中，q 被称为商，r 被称为余数。
   有了这个新的定义，那么C中或者Python中的“取模”，就都能解释了。
   解释C : -10 = (-3) * 3 + (-1)
   解释Python： - 10 = （ ? ） * 3 + 2, 其中，可以推到出来, '?'必须是 - 4(后面验证).即 - 10 = （ - 4） * 3 + 2，才能
   满足定义。
   所以，在不同语言，同一个计算表达式，负数“取模”结果是不同的。我们可以称之为分别叫做正余数和负余数

如果是细心的朋友就发现了，我在发python的图片时，把除数给算了，算到-10/3等于-3.333大概这样的数，那么为什么又会等于-4呢？

那就要回到我们文章刚开始讲整数的四种取整模式了，而python的取整模式可以很明显的看到是负无穷取整，所以等于-4，故定义- 10 = （ -4） * 3 + 2,成立

那么回答一个前面的问题取模和取余一样吗？

答案是不一样的，虽然大部分不严格定义的时候是一样的，但是严格起来就完全不一样了

取余或者取模，都应该要算出商，然后才能得出余数。
本质 1 取整：
取余：尽可能让商，进行向0取整。
取模：尽可能让商，向 - ∞方向取整

故： C中%,本质其实是取余。 Python中%，本质其实是取模。

那么大家还记得刚开始所有取模方式的那个表吗？有的取整方式不一样，但是在一定时候是相同的，正数向0取整和负无穷取整一样

总结：所以为什么我们在C语言当中没有发现这个问题，是因为我们在C语言取模中从来没有取过负数，都是取模取的是正数

文章写作不易：所以兄弟们，给xd赞和关注吧！谢谢了