6016. Excel 表中某个范围内的单元格

题目
Excel 表中的一个单元格 (r, c) 会以字符串 “” 的形式进行表示，其中：

即单元格的列号 c 。用英文字母表中的 字母 标识。 例如，第 1 列用 'A' 表示，第 2 列用 'B' 表示，第 3 列用 'C' 表示，以此类推。 即单元格的行号 r 。第 r 行就用 整数 r 标识。 给你一个格式为 ":" 的字符串 s ，其中 表示 c1 列， 表示 r1 行， 表示 c2 列， 表示 r2 行，并满足 r1 <= r2 且 c1 <= c2 。

找出所有满足 r1 <= x <= r2 且 c1 <= y <= c2 的单元格，并以列表形式返回。单元格应该按前面描述的格式用 字符串 表示，并以 非递减 顺序排列（先按列排，再按行排）。

示例 1：

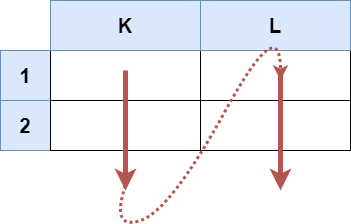
输入：s = “K1:L2”
输出：[“K1”,“K2”,“L1”,“L2”]
解释：
上图显示了列表中应该出现的单元格。
红色箭头指示单元格的出现顺序。

示例 2：

输入：s = “A1:F1”
输出：[“A1”,“B1”,“C1”,“D1”,“E1”,“F1”]
解释：
上图显示了列表中应该出现的单元格。
红色箭头指示单元格的出现顺序。

提示：

s.length == 5
‘A’ <= s[0] <= s[3] <= ‘Z’
‘1’ <= s[1] <= s[4] <= ‘9’
s 由大写英文字母、数字、和 ‘:’ 组成

分析
将行和列的起始位置从字符串中提取出来再循环遍历即可，注意字符与数字之间的转换即可
代码

class Solution {
public:
    vector<string> cellsInRange(string s) {
        string a="", b="";
        int an=0, bn=0;
        int i=0;
        while(s[i] != ':'){
            if(isalpha(s[i]))
                a += s[i];
            else{
                an *= 10;
                an += s[i] - '0';
            }
            i++;
        }
        i++;
        int length = s.size();
        while(i < length){
            if(isalpha(s[i]))
                b += s[i];
            else{
                bn *= 10;
                bn += s[i] - '0';
            }
            i++;
        }
        vector<string> ans;
        
        for(int j=a[0]-'A'; j <= b[0]-'A'; j++){
            for(int i=an; i <= bn; i++){
            	string tmp="";
                char n1 = j + 'A';
                char n2 = i + '0';
                tmp += n1;
                tmp += n2;
                ans.push_back(tmp);
        	}
        }
        
        return ans;
    }
};

6017. 向数组中追加 K 个整数

题目
给你一个整数数组 nums 和一个整数 k 。请你向 nums 中追加 k 个 未 出现在 nums 中的、互不相同 的 正 整数，并使结果数组的元素和 最小 。

返回追加到 nums 中的 k 个整数之和。

示例 1：

输入：nums = [1,4,25,10,25], k = 2
输出：5
解释：在该解法中，向数组中追加的两个互不相同且未出现的正整数是 2 和 3 。
nums 最终元素和为 1 + 4 + 25 + 10 + 25 + 2 + 3 = 70 ，这是所有情况中的最小值。
所以追加到数组中的两个整数之和是 2 + 3 = 5 ，所以返回 5 。

示例 2：

输入：nums = [5,6], k = 6
输出：25
解释：在该解法中，向数组中追加的两个互不相同且未出现的正整数是 1 、2 、3 、4 、7 和 8 。
nums 最终元素和为 5 + 6 + 1 + 2 + 3 + 4 + 7 + 8 = 36 ，这是所有情况中的最小值。
所以追加到数组中的两个整数之和是 1 + 2 + 3 + 4 + 7 + 8 = 25 ，所以返回 25 。

提示：

1 <= nums.length <= 10^5
1 <= nums[i], k <= 10^9

分析
排序+贪心，根据贪心的思路，我们每次选用的都应该选取最小的，所以我们可以先将nums排序，然后求取即可

但是这道题有个坑点：直接遍历会超时！！！通过观察我们可以发现，如果我们把每一个符合要求的位置看作区间，那么这个问题就变成的等差序列的和的问题，那么我们可以按照以下公式来计算
$$\frac{(起始数值+结束数值)\ast 个数}{2}$$
那么问题就变为了如何求符合要求的区间——如果nums[0]>1，说明从1到nums[0]-1有符合条件的区间，如果nums[0]=1，那么我们也可以通过遍历排好序的nums来寻找区间，尤其注意的是如果遍历到了尾部，仍然没有取够k个数，那么从nums[nums.size()-1]+1位置，到取够k个数之前全为符合要求的区间
代码

class Solution {
public:
    long long minimalKSum(vector<int>& nums, int k) {
        long long ans=0;
        int length = nums.size();
        sort(nums.begin(),nums.end());
        if(nums[0] > 1 && k > 0){
            if(k > nums[0]-1){
                if(nums[0] % 2){
                    ans += (long long)(nums[0]-1) / 2 * (long long)nums[0];
 
                }
                else{
                    ans += (long long)nums[0] / 2 * (long long)(nums[0]-1);
      
                }
                k -= nums[0]-1;
   
            }else{
                ans += (long long)k * (long long)(k + 1) / 2;
                k = 0;

            }
            
        }

        if(k > 0){
            for(int i=0; i < length-1 && k > 0; i++){
                if(nums[i+1] == nums[i]){
                    continue;
                }
                int d = nums[i+1] - nums[i]-1;

                if(k > d){
                    if((nums[i+1] + nums[i]) % 2 == 0){
                        ans += (long long)(nums[i+1] + nums[i]) / 2 * d;
                    }else{
                        ans += d / 2 * (long long)(nums[i+1] + nums[i]);
                    }  
         
                    k -= d;
                    
                }else{
                    int end = nums[i]+k+1;
                    
                    if(k % 2){
                        ans += (long long)(nums[i] + end) / 2 * k;
                    }else{
                        ans += k / 2 * (long long)(nums[i] + end);
                    }
                    k=0;
                }
            } 
        }
        cout<<k<<endl;
        if(k > 0){
            int end = nums[length-1] + k + 1;
            if(k % 2){
                ans += (long long)(nums[length-1] + end) / 2 * k;
            }else{
                ans += k / 2 * (long long)(nums[length-1] + end);
            }
        }
        return ans;
    }
};

6018. 根据描述创建二叉树

题目
给你一个二维整数数组 descriptions ，其中 descriptions[i] = [parenti, childi, isLefti] 表示 parenti 是 childi 在 二叉树 中的 父节点，二叉树中各节点的值 互不相同 。此外：

如果 isLefti == 1 ，那么 childi 就是 parenti 的左子节点。
如果 isLefti == 0 ，那么 childi 就是 parenti 的右子节点。
请你根据 descriptions 的描述来构造二叉树并返回其 根节点 。

测试用例会保证可以构造出 有效 的二叉树。

示例 1：

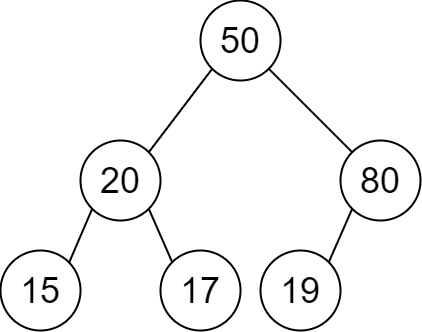
输入：descriptions = [[20,15,1],[20,17,0],[50,20,1],[50,80,0],[80,19,1]]
输出：[50,20,80,15,17,19]
解释：根节点是值为 50 的节点，因为它没有父节点。
结果二叉树如上图所示。

示例 2：

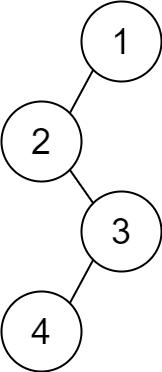
输入：descriptions = [[1,2,1],[2,3,0],[3,4,1]]
输出：[1,2,null,null,3,4]
解释：根节点是值为 1 的节点，因为它没有父节点。
结果二叉树如上图所示。

提示：

1 <= descriptions.length <= 10^4
descriptions[i].length == 3
1 <= parenti, childi <= 10^5
0 <= isLefti <= 1
descriptions 所描述的二叉树是一棵有效二叉树

分析
这道题如果树的相关知识掌握牢固很快就能想到这是一个常规的构建二叉树的题目，结合代码来看，首先我们用变量mp来存储数值和结点的映射关系以便于连接时可以迅速找到所需的结点，同时使用pt来表示父子关系，最后返回的时pt为0的点，即没有父节点的点，即根结点

代码

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    TreeNode* createBinaryTree(vector<vector<int>>& descriptions) {
        map<int, TreeNode*> mp;
        map<int, int> pt;
        set<int> st;
        TreeNode* ans;
        for(auto & dsp:descriptions){
            pt[dsp[1]] = dsp[0];
            if(st.count(dsp[0])){
                TreeNode* head;
                head = mp[dsp[0]];
                if(st.count(dsp[1])){
                    if(dsp[2]==1){
                        head->left = mp[dsp[1]];
                    }else{
                        head->right = mp[dsp[1]];
                    }
                }else{
                    st.insert(dsp[1]);
                    TreeNode* l;
                    l = new TreeNode;
                    l->val = dsp[1];
                    mp[dsp[1]] = l;
                    if(dsp[2]==1){
                        head->left = l;
                    }else{
                        head->right = l;
                    }
                };
            }else{
                st.insert(dsp[0]);
                TreeNode* head;
                head = new TreeNode;
                head->val = dsp[0];
                mp[dsp[0]] = head;
                if(st.count(dsp[1])){
                    if(dsp[2]==1){
                        head->left = mp[dsp[1]];
                    }else{
                        head->right = mp[dsp[1]];
                    }
                }else{
                    st.insert(dsp[1]);
                    TreeNode* l;
                    l = new TreeNode;
                    l->val = dsp[1];
                    mp[dsp[1]] = l;
                    if(dsp[2]==1){
                        head->left = l;
                    }else{
                        head->right = l;
                    }
                }
            }
        }
        for(auto & dsp:descriptions){
            if(pt[dsp[0]]==0){
                ans = mp[dsp[0]];
            }
        }
        return ans;
    }
};

6019. 替换数组中的非互质数

题目
给你一个整数数组 nums 。请你对数组执行下述操作：

从 nums 中找出 任意 两个 相邻 的 非互质 数。
如果不存在这样的数，终止 这一过程。
否则，删除这两个数，并 替换 为它们的 最小公倍数（Least Common Multiple，LCM）。
只要还能找出两个相邻的非互质数就继续 重复 这一过程。
返回修改后得到的 最终 数组。可以证明的是，以 任意 顺序替换相邻的非互质数都可以得到相同的结果。

生成的测试用例可以保证最终数组中的值 小于或者等于 108 。

两个数字 x 和 y 满足 非互质数 的条件是：GCD(x, y) > 1 ，其中 GCD(x, y) 是 x 和 y 的 最大公约数 。

示例 1 ：

输入：nums = [6,4,3,2,7,6,2] 输出：[12,7,6] 解释：

• (6, 4) 是一组非互质数，且 LCM(6, 4) = 12 。得到 nums = [12,3,2,7,6,2] 。
• (12, 3) 是一组非互质数，且 LCM(12, 3) = 12 。得到 nums = [12,2,7,6,2] 。
• (12, 2) 是一组非互质数，且 LCM(12, 2) = 12 。得到 nums = [12,7,6,2] 。
• (6, 2) 是一组非互质数，且 LCM(6, 2) = 6 。得到 nums = [12,7,6] 。 现在，nums 中不存在相邻的非互质数。 因此，修改后得到的最终数组是 [12,7,6] 。 注意，存在其他方法可以获得相同的最终数组。

示例 2 ：

输入：nums = [2,2,1,1,3,3,3]
输出：[2,1,1,3]
解释：

• (3, 3) 是一组非互质数，且 LCM(3, 3) = 3 。得到 nums = [2,2,1,1,3,3] 。
• (3, 3) 是一组非互质数，且 LCM(3, 3) = 3 。得到 nums = [2,2,1,1,3] 。
• (2, 2) 是一组非互质数，且 LCM(2, 2) = 2 。得到 nums = [2,1,1,3] 。
  现在，nums 中不存在相邻的非互质数。
  因此，修改后得到的最终数组是 [2,1,1,3] 。
  注意，存在其他方法可以获得相同的最终数组。

提示：

1 <= nums.length <= 10^5
1 <= nums[i] <= 10^5
生成的测试用例可以保证最终数组中的值 小于或者等于 108 。

分析
题目中看似条件众多，其实可以把他当作一个模拟题的，即按照题目所说的去做就好。我们的做法是先建一个新的vector，然后把他当作栈，通过遍历将nums的元素添加到新建的vector中，然后按照题目要求算最小公倍数和最大公约数并对数据进行修改即可。
代码

class Solution {
public:
    vector<int> replaceNonCoprimes(vector<int>& nums) {
        vector<int> stk{nums[0]};
        for(int i=1; i < nums.size(); i++){
            stk.push_back(nums[i]);
            while(stk.size() > 1){
                int x = stk.back(), y=stk[stk.size()-2];
                int g = gcd(x, y);
                if(g == 1){
                    break;
                }
                stk.pop_back();
                stk.back() *= x / g;
            }
        }
        return stk;
    }
};

最后

以上就是怕孤单芝麻为你收集整理的LeetCode刷题——LeetCode第 283 场周赛6016. Excel 表中某个范围内的单元格6017. 向数组中追加 K 个整数6018. 根据描述创建二叉树6019. 替换数组中的非互质数的全部内容，希望文章能够帮你解决LeetCode刷题——LeetCode第 283 场周赛6016. Excel 表中某个范围内的单元格6017. 向数组中追加 K 个整数6018. 根据描述创建二叉树6019. 替换数组中的非互质数所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。