Python自制随机数生成算法

在Python中生成随机数, 一般会调用random模块, 但random模块内也有自己的算法实现。
如何设计自己的算法呢?本文将介绍。

1.算法

生成随机数, 首先要有一个随机数种子seed, 然后根据这个种子, 推导出剩余的数字, 也就是伪随机数。
一种方法是将种子经过一定的变换, 再除以一个数,
得到的余数作为新的种子。这种方法也称线性同余算法。

2.程序实现

程序生成在0至1范围内的500个随机数。

from time import perf_counter

seed = perf_counter()
k=5.6;b=3.5
i=1
def random():
    global seed
    seed=seed*k+b
    if seed > 10**10:
        seed=perf_counter() # 加入时间的随机因素
    return seed % i

l=[]
for j in range(500):
    l.append(random())
    k=random()*5.6 # 变化k, 避免随机数重复

3.检验自制的算法

对随机数算法的要求是随机数的重复周期很长, 且在生成的区间内分布均匀。
首先生成包含500个随机数的列表，计算随机数的期望和方差：

e = sum(l)/len(l) # 数学期望
a = e # 平均值
d = sum((x-a)**2 for x in l2) /len(l2)
print("自制随机数的期望和方差:",e,d) # 结果为 0.50298433624 0.080202207010
l2=[random2() for i in range(500)]
e2 = sum(l2)/len(l2)
a2 = e2
d2 = sum((x-a2)**2 for x in l2) /len(l2)
print("内置random函数的期望和方差:",e2,d2) # 结果为 0.51050220327 0.08014568868

如果前面的检验还不够直观，用matplotlib库把500个随机数的列表“画”出来：

import matplotlib.pyplot as plt
from random import random as random2
# --snip-- 前面部分省略
plt.hist(l,bins=len(l)//5)
plt.show()
# 和真正的random函数对照
l2=[random2() for i in range(500)]
plt.hist(l2,bins=len(l2)//5)
plt.show()

结果如下, 这是自制的random()函数:

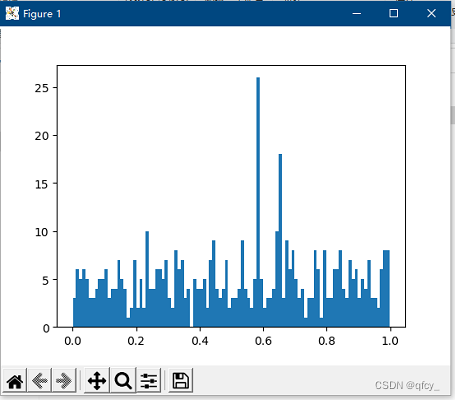
而测试random模块中的random函数, 结果如下:

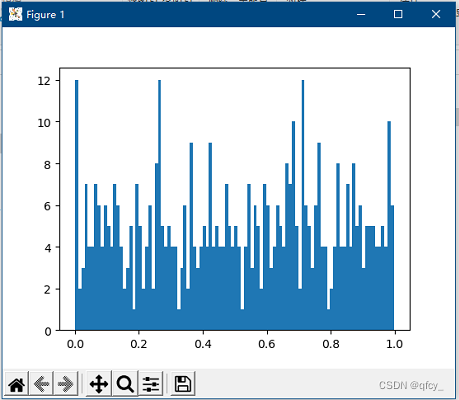
会发现, 前述自制的随机数生成算法生成的值比较均匀, 比较好地模拟了random模块中的随机数生成。
如果有更好的方法, 欢迎在评论区交流!

最后

以上就是轻松黑裤为你收集整理的Python自制随机数生成算法的全部内容，希望文章能够帮你解决Python自制随机数生成算法所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。