哈希加密matlab,图像加密算法之基于Hash函数和多混沌系统的加密

为了实现对数字图像的有效保护，我们提出一种基于Hash函数和多混沌系统的图像加密算法。该图像加密算法通过像素置乱、灰度置乱及灰度扩散实现图像文件加密。

一、混沌系统

1、Lorenz混沌系统

本文在像素置乱阶段使用Lorenz混沌系统，它的动力学方程为：

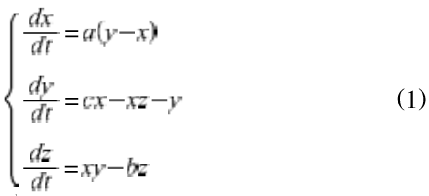
当a=10，b=8/3，c=28时出现混沌吸引子，系统进入混沌状态，如图1(a)所示。Lorenz系统对初始条件是极其敏感的，两个误差仅为10.15的初始条件，随着运行时间的增加，运行轨迹

会出现极大的偏差，并且呈现无规则性。

2、 Logistic混沌系统

灰度置乱阶段采用Logistic系统产生随机序列，其原型为：

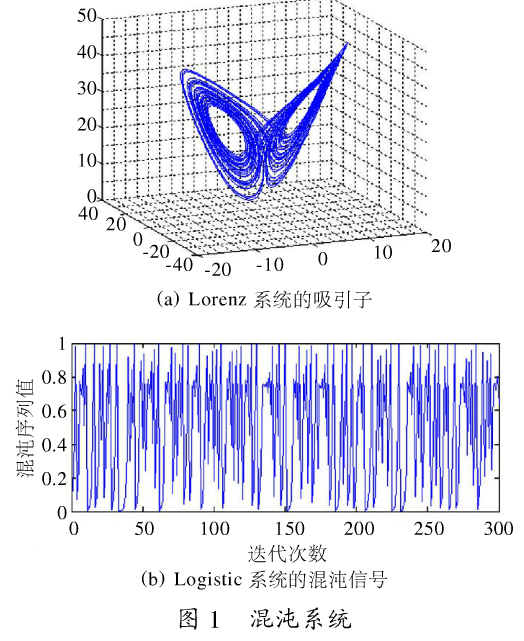
式中：xn映射变量，0≤xn≤1，μ——系统参数，0≤μ≤4。当3.5699456…≤μ≤4时，系统进入混沌状态。文中所采用的Logistic混沌系统中μ取为3.9999。图1(b)出示了当x0=0.123456781时的混沌实数序列图，从图中可以看出，序列呈现出一种近化随机的状态。

二、 图像文件加密方案

1、图像像素置乱

图像像素置乱的主要目的是为了有效地打乱像素位置。常用的像素置乱方法主要有两种，一是直接对图像的像素点坐标位置进行线性变换，如Arnold变换，幻方变换，3D猫映射，二是先对图像进行分块，然后再置乱，但此种方法的安全性不高。本文利用Hash表来实现像素位置的变换，置乱表由Hash函数产生，函数的基本描述为h(c,λ,d,s,L)，其中C代表Lorenz混沌系统，λ是变换参数，d是采样步长，s是采样起始点，L是Hash表长度。

假设选择的图像大小为MxN，图像的置乱步骤为：

(1)由Lorenz混沌系统以及初始密钥产生混沌序列；

(2)根据Hash函数，h(c,λ,d,s,L)构造规则及混沌序列构造散列表h1，其中d1是h1的采样步长；

(3)根据Hash函数h(c,λ,d,s,L)构造规则及混沌序列构造散列表h2，其中d2是h2的采样步长；

(4)根据h1和h2先后对图像的行列进行变换。

2、图像灰度置乱

在现代加密体制中，置换和替代仍是加密体制的两个基本构造模块，单独的置换和替代也能达到一定的加密效果，但如果能两者兼顾则效果更好。在上节中我们利用Hash函数对像素的位置进行了置乱，但这并不能改变灰度值，加密图像和原图像仍具有相同的灰度统计直方图，因此必须对图像灰度进行替代，以抵抗攻击者的统计分析。由于图像灰度的组成元素是0～255的整数值，本文用一种类似初等密码中的多表代替密码对灰度数值进行置乱，使其不再保持原来的灰度值。

对大小为M×N的灰度图像，图像灰度置乱步骤为：

(1)根据初始条件x0由Logistic混沌系统生成一条长度为l的随机序列S，并将其变换为[0,255]之间的整数值。

(2)将图像的灰度矩阵按行优先拉伸成一维数组，然后与序列S中的值对应进行比特异或，得到序列S；

(3)把S按列优先还原成灰度矩阵。

若序列S的长度l

加密算法中像素灰度值的替代处理实际上也是灰度空间的置换，替代过程使灰度值相近的两个相邻像素，在经过处理后，灰度值相差很大，彻底打乱了相邻像素的灰度相关性。

3、像素灰度值的扩散

仅仅对图像进行像素和灰度的置乱容易受到选择明文的攻击，攻击者可以选择单个像素点的变化，而得到像素位置变化的对应关系，而扩散机制的引入则可以很好地避免这一弱点，良好的扩散机制不仅可以使明文的一位灰度值发生变化时能够迅速的引起其后的所有灰度值发生变化，有效地抵御差分攻击，而且还能起到很好的灰度置乱作用。为此，引入如下扩散公式：

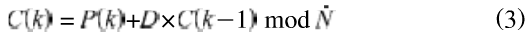
式中：P(k)——待处理的像素值，c(k一1)——上一个处理过的像素的灰度值，D——扩散因子，x0——初始密钥面控制生成；N——灰度级。

4、图像文件加密和解密过程

根据以上分析，可得到图像文件加密的基本流程，如图2所示。

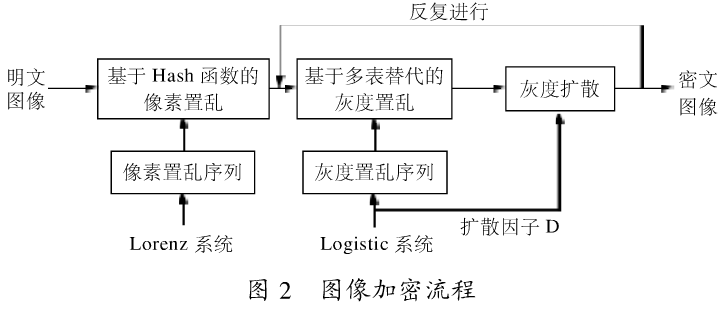
加密步骤描述如下：

设图像像素所表示的二维数组为G=(gi)M×N，其中M×N是图像的大小，gi为坐标(i,j)处的像素值。

(1)由Lorenz系统产生初始值，将明文图像按2—1节所示的方法进行像素置乱，置乱后输出图像为G’；

(2)由Logistic系统产生混沌序列并按2—2节的多表代替规则对G’进行灰度置乱，置乱后输出的图像为G”；

(3)对G”进行灰度扩散，输出即为密文图像；出于安全性的考虑可对(2)，(3)两步重复多次。

解密过程与加密过程相似，其中扩散的逆变换公式为：

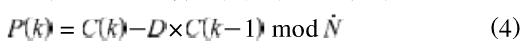
三、模拟实验及性能分析

1、实验结果

本文的实验平台为Matlab 7.0，选取256×256的Lena灰度图像进行实验。其中Lorenz系统的密钥(x0,λ,d,s)=(0.42，10的10次方，3，300)，面为初始值。Logistic系统的初始值为0.12345678901234，随机序列S的长度l=2000。

加解密效果如图3所示，其中图3(a)为明文图像，图3(b)为加密后图像，图3(c)是Logistic系统密钥取为0.12345678901235时的解密图像，图3(d)为密钥正确时的解密图像。

2、统计分析

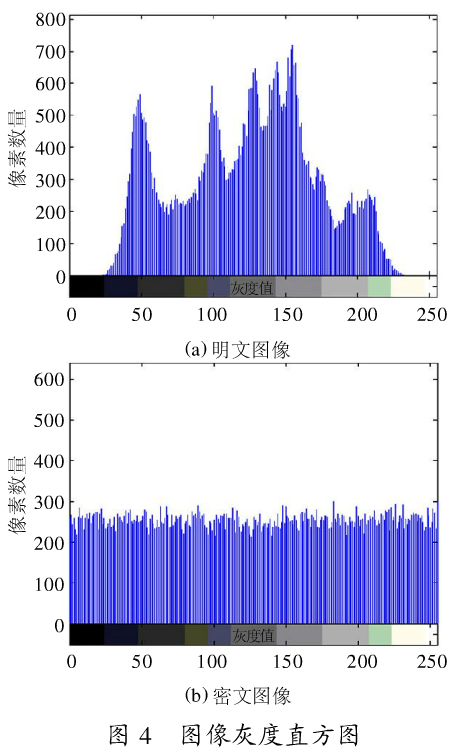
(1)灰度直方图

直方图是图像的重要统计特征，它直观地反映了数字图像的每一灰度级与该灰度级出现频率的对应关系。图4(a)是原始图像(图3(a))的像素灰度直方图，图4(b)则对应密文图像(图3(b))。根据仿真显示，密文与明文的直方图区别很大，密文的直方图分布非常均匀，表明该方案能够有效抵御基于像素值统计的攻击。

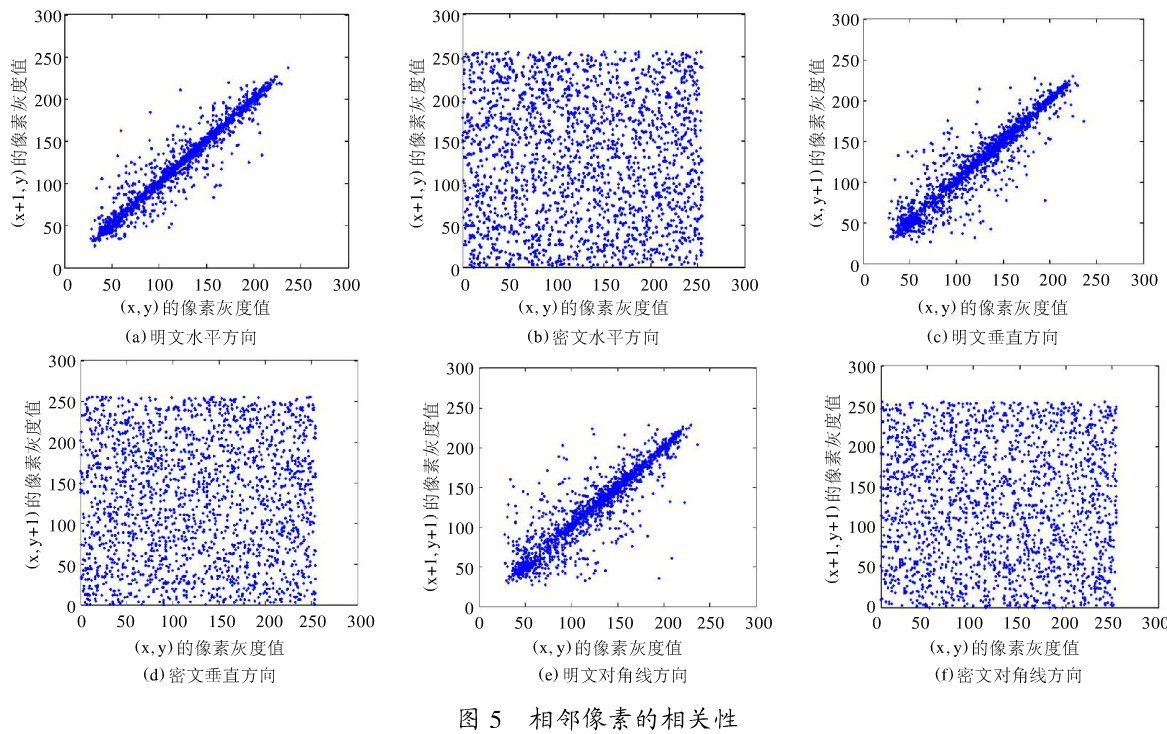
(2)相邻像素的相关性

由图像的特性可知，一幅图像中相邻像素间存在较大的相关性，这也使得攻击者经常利用统计分析的方法对图像进行密码分析，好的加密算法应当有效地打乱这种相关性。为此，可以借助概率论的相关系数来衡量相邻像素的相关性，相关系数定义如下：

式中：cov(x，y))——协方差，D(x) ——方差，E(x)——均值，xy——相邻像素的灰度值。

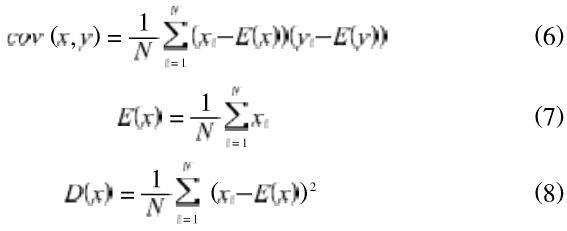
图5是通过仿真实验对明文和密文中水平、垂直和对角线方向相邻像素的相关性检测。从图中可以看出，明文的相邻像素的相关性很强，而密文则不同，不管是水平、垂直还是对角线方向分布都比较均匀，这说明密文有效地掩盖了图像的统计特征。

3、差分攻击

通常攻击者会通过图像的一点微小变化，比如只改变一个像素，来观察加密后图像的变化情况，进而发掘明密文之间的关系。为了测试一个像素的改变对整个密文图像的影响，引入如下两个量：像素变化率(NPCR)和归一化平均变化强度(UACI)。对于只有一个像毒声别的两幅密文图像C1和C2，C1(i,j)和C2(i,j)代表两幅图像(i,j)点的像素强度，D是一个和c1，c2同样大小的二值矩阵，若C1(i,j)≠C2(i,j)，则D(i,j)=1，否则D(i,j)=0。

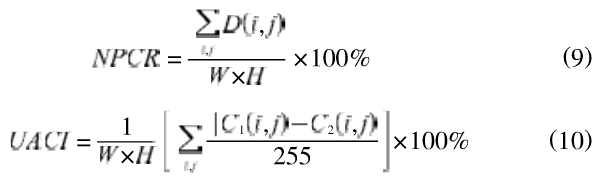
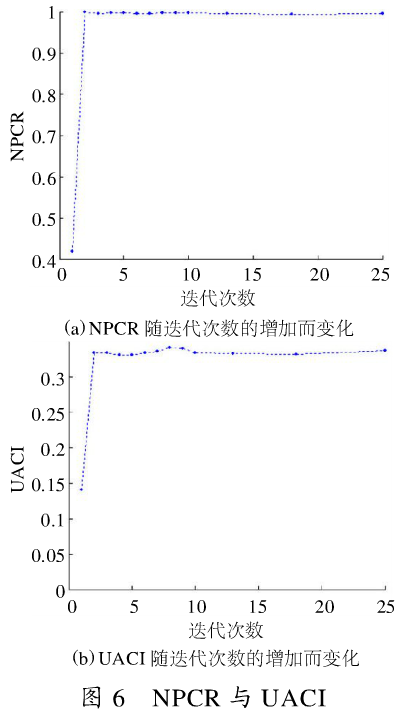
其中，W和H是C1，C2的大小。将明文图像中的第5个像素值为155改为156，仿真实验结果如图6所示，在参数不变的情况下，当迭代两次以后，NPCR≈1。两幅只有一位像素不同的

图像，随着加密次数的增加，密图变的几乎完全不同，原图的差别扩散到了密图的整个区域，因此可以增加迭代次数来提高加密的安全性，但同时加密的时间复杂度也会随之升高。

4、密钥空间及敏感性分析

(1)密钥空间

在像素置乱阶段，对Lorenz混沌初始条件，散列函数，以及参数见进行穷尽攻击是不可能的，假设对于一个M×N的256级的灰度图像，行变换序列和列变换序列分别有M！和N!种，因此，要加密一个大小为M×N且灰度级为256的图像，可用的初始序列和变换序列有M!×N！种情况。在灰度置乱阶段，由于Logistic混沌随机序列了的引入，当S的长度为L时，理论上有256L个不同的值，同时厶的取值可以是从1到图像向量拉伸的长度M×N，总的组合种类数为：

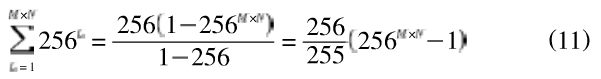
可见，若把像素置乱与灰度置乱结合起来的密钥空间按照目前的计算条件对其进行穷举攻击是根本不可能的。

(2)密钥敏感性

好的图像加密算法在加密过程中应对密钥非常敏感，密钥的一点细微变化都能引起密文的极大变化，这包括两方面含义：一是加密密钥的细微改变，应使两幅密文图像几乎完全不同；二是解密密钥的细微改变，其解密过程将失败。

仿真实验结果表明，当Logistic系统的初始密钥分别为0.12345678901234和0.12345678901235时，加密后的两幅图像中有99.26%的像素灰度值不相同，密钥的微小变化导致密文几乎完全不同。同样，在解密过程中，密钥的微小变化也会导致解密的失败，如图3，图3(a)为明文图像，图3(b)是初始密钥为0.12345678901234加密图像，图3(c)是解密密钥取为0.12345678901235时的解密图像，从两幅图像看，解密几乎完全失败。因此本文算法在加解密过程中都有良好的密钥敏感性。

小知识之扩散因子

扩散因子：这是一个用于评估期刊影响力的学术指标，显示总被引频次扩散的范围。具体意义为期刊当年每被引100次所涉及的期刊数。

扩散因子= 总被引频次涉及的期刊数×100/总被引频次