机器学习笔记（五）机器学习参数

 

第六章，机器学习诊断法，改进机器学习算法，寻找合适的

　　上半部分：机器学习的建议

1.当加入新的例子发现之前的算法是错误的，改进方法：

• 寻找更多的训练集
• 减少特征参数或修改特征参数，增加没有考虑到的特征
• 增加多项式
• 改变lambda的大小等等

2.判断一个算法是否正确

• 将数据集分成训练数据和测试数据（7:3，随机选择）；
• 用训练数据求得theta；
• 用测试数据求误差(即求J函数值，不加正则化)；
• 求误差率（预测错误的/总的测试个数*100%）；

3.选择模型（选择h函数的多项式次数d）：将数据分成三个部分，对每一个可能的多项式进行如下计算

• 训练集（60%）：用来求theta
• 交叉验证集cross validation（20%）：测试训练集的各种多项式的theta的误差率，选择最小误差率的多项式（选择）
• 测试集（20%）：验证测试集所得的h函数对新的数据的拟合情况（和之前的不一样）（看结果）

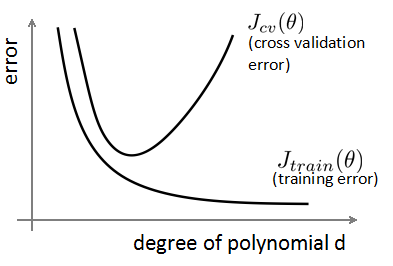
注意：不要用测试集做选择多项式后，再用测试集做测试拟合情况，因为测试集已经用来选择模型，不再是新数据！！

4.高偏差和高方差

高偏差-欠拟合：训练集和验证集的误差都很大。

高方差-过拟合：训练集的误差很小，验证集的误差很大。

 5.正则化的lambda

lambda太大欠拟合，太小过拟合

6.选择lambda的方法

猜测一些值0，0.01,0.02，……，10.24（2倍步长增长）

然后用3中的方法找最好的lambda。

 

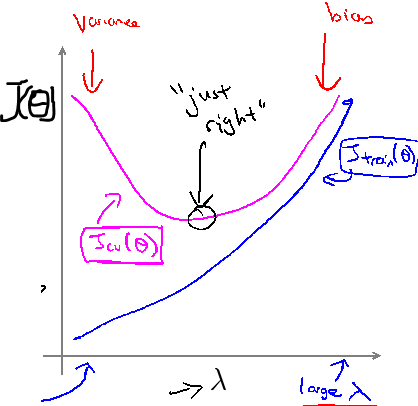
7.学习曲线（随着训练集个数的变化），可以用来区分高偏差和高方差

如果一个学习算法处于高偏差（欠拟合），则增大训练集的个数不会有什么帮助，训练集和验证集的J都会很大，见下图（最后随着m增大，曲线已经变成水平）：（所以不是只要增大训练集就可以！）

欠拟合图像特征：随着m增加两条曲线靠近，并且值都比较大。

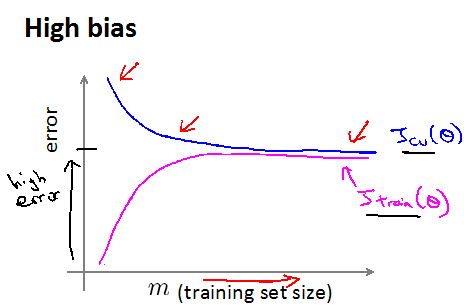
如果一个学习算法处于高方差（过拟合），则增大训练集的个数会有帮助，训练集J会增加（但增加幅度小一点），验证集的J会越来越小，见下图（开始两个曲线有很大的差距，最后随着m增大，两个曲线会慢慢靠近）：

过拟合图像特征：训练集曲线一般较小，且两曲线之间距离大点，值都比较小。

 

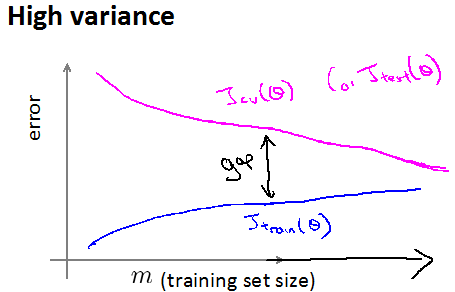
注意：图像的横坐标m的意思是训练集的个数，指的是训练集从1-m，验证集的图像使用的个数不变。

 

 8.回到最出的问题：当加入新的例子发现之前的算法是错误的，改进方法，并且适用情况：

• 寻找更多的训练集：只适用于高方差（过拟合），画出学习曲线，看看是不是（即验证集应该比训练集误差大）
• 减少特征参数：只适用于高方差（过拟合）
• 增加没有考虑到的特征参数：适用于高偏差（欠拟合），即算法比较简单，需要增加因素
• 增加多项式：适用于高偏差（欠拟合），类似增加特征参数
• 减小ambda的大小：适用于高偏差（欠拟合）
• 增大ambda的大小适用于高方差（过拟合）

9.对于神经网络的问题

如果结构简单，很容易出现欠拟合的情况；如果结构复杂，很容易出现过拟合的情况（用正则化的方法改进）。一般使用正则化改进的稍复杂的结构。

关于选隐藏层的层数和每一层的单元个数，同样可以使用交叉验证集的方法，即3中的方法。

一定要先确定是高方差还是高偏差，然后在进行修改，不然只能做无用功！

 

 

 

　　下半部分：机器学习系统的设计

 

1.解决一个垃圾邮件分类器

确定特征参数x：预先选择一些单词（比如buy、discount可能是垃圾邮件的单词，now、sunbaofeng可能不是垃圾邮件的单词，一般是先遍历训练集，选出出现次数最多前10000-50000的单词），形成一个X向量，如果邮件中有这个单词，对应位置为1，否则0。

如何更加精确地解决问题：

• 收集更多的数据
• 把发件人的信息、标题作为特征
• 从内容中找更加复杂的特征，比如discount和discounts处理成一个单词、大小写
• 处理拼写错误

2.误差分析（error analysis）

　　在刚接触一个新问题时，应该先选用一个简单的系统，然后进行交叉验证集的方法画学习曲线进行改正，这是一个强有力的工具，来进行修改。（开始时不知道应该把时间花在哪个方面提高准确性）

　　误差分析：观察验证集中被算法错误预测的数据，从中得到启发应该怎么样修改算法（增加变量等），看看1中的4中方法更应该选择哪个！

　　当有一些想法改进算法时，应该用交叉验证集的方法比较错误率的大小（评估度量值），来确定是不是采用，而不是通过臆测觉得对就采用！

 

3.偏斜类（skewed classes）：在测试集中只有很少的部分的y=1或0，偏向一类，可能预测函数会出现类似直接返回0的情况，处理一些现实中分类的比例较大的。

查准率（precision）和召回率（recall）处理偏斜类，y=1表示某种稀缺的值，比如y=1表示患癌症（患癌症的人较少）。

查准率（precision）和召回率（recall）越大越说明我们预测的准确，如果算法计算后的两者有一个非常小的，则说明这个算法模型不怎么好。

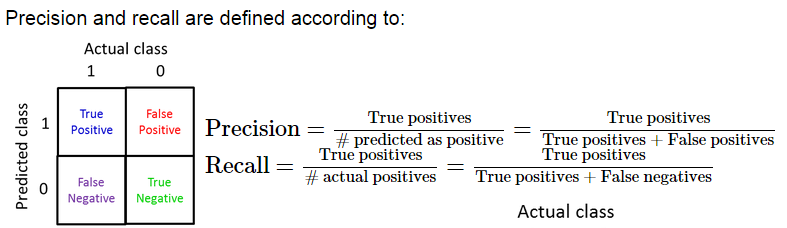
当改变算法时，因为查准率（precision）和召回率（recall）通常会一个变大，一个变小，所以不像只有一个评估度量值时，可以准确的确定新的算法是不是更好。

如何使用查准率（precision）和召回率（recall）来评估算法是不是更好呢？

使用F1值：（p代表precision，r代表recall）越接近1越好（仔细想想不同问题不同考虑，只要两个算法不接近0时，可以直接看p和r的值，觉得F1值不一定对）

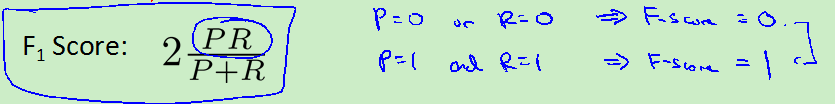
 4.当选择的特征足够多（可以把所要求的问题的信息都包含），而且算法较复杂，即多项式复杂，就可以避免高偏差。并且有很大的训练集（数量比特征多得多），就可以避免高方差，这是很好的求解算法的条件。

 

 

代码

1.特征缩放和归一化

function [X_norm, mu, sigma] = featureNormalize(X)
    mu = mean(X);
    X_norm = bsxfun(@minus, X, mu);%@minus表示减

    sigma = std(X_norm);    %标准差
    X_norm = bsxfun(@rdivide, X_norm, sigma);%@rdivide表示除
end

2.由列向量x，形成[x,x^2,x^3……,x^p]

function [X_poly] = polyFeatures(X, p)
    X_poly = zeros(numel(X), p);
    X_poly(:,1) = X(:,1);
    for i=2:p
        X_poly(:,i)=X_poly(:,i-1) .* X_poly(:,1);
    end;
end

3.线性回归代价函数

function [J, grad] = linearRegCostFunction(X, y, theta, lambda)
    m = length(y); 
    J = 0;
    grad = zeros(size(theta));
    J=sum((X*theta-y) .^2)/(2.0*m)+ (theta' *theta-theta(1)*theta(1))*lambda/(2*m);

    grad=(X'*(X*theta-y))/m +theta*lambda/m;
    grad(1)-=theta(1)*lambda/m;
    grad = grad(:);
end

4.高级梯度函数调用

function [theta] = trainLinearReg(X, y, lambda)
    initial_theta = zeros(size(X, 2), 1); 
    costFunction = @(t) linearRegCostFunction(X, y, t, lambda);
    options = optimset('MaxIter', 200, 'GradObj', 'on');
    theta = fmincg(costFunction, initial_theta, options);

end

5.求学习曲线，随着m的变化的代价值

function [error_train, error_val] =learningCurve(X, y, Xval, yval, lambda)%X,y是训练集，Xval,yval是验证集
    m = size(X, 1);
    error_train = zeros(m, 1);%保存训练集的代价
    error_val   = zeros(m, 1);%保存验证集的代价

    for i=1:m
        theta=trainLinearReg(X(1:i,:), y(1:i,:), lambda);
        error_train(i)=linearRegCostFunction(X(1:i,:), y(1:i,:), theta, 0);%用0，而不是lambda，容易出错，不如另写一个函数
        error_val(i)=linearRegCostFunction(Xval, yval, theta, 0);%用0，而不是lambda
    end;

end

6.选择lambda函数，保存不同lambda的代价值

function [lambda_vec, error_train, error_val]=validationCurve(X, y, Xval, yval)
    lambda_vec = [0 0.001 0.003 0.01 0.03 0.1 0.3 1 3 10]';
    error_train = zeros(length(lambda_vec), 1);
    error_val = zeros(length(lambda_vec), 1);
    for i=1:length(lambda_vec)
        lambda = lambda_vec(i);
        theta=trainLinearReg(X, y, lambda);
        error_train(i)=linearRegCostFunction(X, y, theta, 0);
        error_val(i)=linearRegCostFunction(Xval, yval, theta, 0);
    end;
end

7.整体代码，不用看

    clear ; close all; clc;
    load ('ex5data1.mat');

    m = size(X, 1);
    %figure 9;
    %plot(X, y, 'rx', 'MarkerSize', 10, 'LineWidth', 1.5);
    %xlabel('Change in water level (x)');
    %ylabel('Water flowing out of the dam (y)');

    %theta = [1 ; 1];
    %[J, grad] = linearRegCostFunction([ones(m, 1) X], y, theta, 1);

    %lambda = 0;
    %[theta] = trainLinearReg([ones(m, 1) X], y, lambda);

    %plot(X, y, 'rx', 'MarkerSize', 10, 'LineWidth', 1.5);
    %xlabel('Change in water level (x)');
    %ylabel('Water flowing out of the dam (y)');
    %hold on;
    %plot(X, [ones(m, 1) X]*theta, '=', 'LineWidth', 2)
    %hold off;

    %lambda = 0;
    %[error_train, error_val] = ...
        learningCurve([ones(m, 1) X], y, ...
                      [ones(size(Xval, 1), 1) Xval], yval, ...
                      lambda);

    %plot(1:m, error_train, 1:m, error_val);
    %title('Learning curve for linear regression');
    %legend('Train', 'Cross Validation');
    %xlabel('Number of training examples');
    %ylabel('Error');
    %axis([0 13 0 150])

    %for i = 1:m
    %    fprintf('  t%dtt%ft%fn', i, error_train(i), error_val(i));
    %end


    p = 8;

    % Map X onto Polynomial Features and Normalize
    X_poly = polyFeatures(X, p);
    [X_poly, mu, sigma] = featureNormalize(X_poly);  % Normalize
    X_poly = [ones(m, 1), X_poly];                   % Add Ones
        %数据必须做同样的操作！
    % Map X_poly_test and normalize (using mu and sigma)
    X_poly_test = polyFeatures(Xtest, p);
    X_poly_test = bsxfun(@minus, X_poly_test, mu);
    X_poly_test = bsxfun(@rdivide, X_poly_test, sigma);
    X_poly_test = [ones(size(X_poly_test, 1), 1), X_poly_test];         % Add Ones

    % Map X_poly_val and normalize (using mu and sigma)
    X_poly_val = polyFeatures(Xval, p);
    X_poly_val = bsxfun(@minus, X_poly_val, mu);
    X_poly_val = bsxfun(@rdivide, X_poly_val, sigma);
    X_poly_val = [ones(size(X_poly_val, 1), 1), X_poly_val];           % Add Ones


    %lambda = 0;
    %[theta] = trainLinearReg(X_poly, y, lambda);

    % Plot training data and fit
    %figure(1);
    %plot(X, y, 'rx', 'MarkerSize', 10, 'LineWidth', 1.5);
    %plotFit(min(X), max(X), mu, sigma, theta, p);
    %xlabel('Change in water level (x)');
    %ylabel('Water flowing out of the dam (y)');
    %title (sprintf('Polynomial Regression Fit (lambda = %f)', lambda));


    %hold off;
    lambda =2;
    figure(1);
    [error_train, error_val] = ...
        learningCurve(X_poly, y, X_poly_val, yval, lambda);
    plot(1:m, error_train, 1:m, error_val);

    title(sprintf('Polynomial Regression Learning Curve (lambda = %f)', lambda));
    xlabel('Number of training examples')
    ylabel('Error')
    axis([0 13 0 100])
    legend('Train', 'Cross Validation')


    %[lambda_vec, error_train, error_val] = ...
    %    validationCurve(X_poly, y, X_poly_val, yval);

    %close all;
    %plot(lambda_vec, error_train, lambda_vec, error_val);
    %legend('Train', 'Cross Validation');
    %xlabel('lambda');
    %ylabel('Error');


    %for i = 1:length(lambda_vec)
    %    fprintf(' %ft%ft%fn', ...
    %            lambda_vec(i), error_train(i), error_val(i));
    %end

    %fprintf('Program paused. Press enter to continue.n');
    %pause;