二维伪随机序列结构光编码

        如果一个序列，一方面它是可以预先确定的，并且是可以重复地生产和复制的；一方面它又具有某种随机序列的随机特性（即统计特性），我们便称这种序列为伪随机序列。因此可以说，伪随机序列是具有某种随机特性的确定的序列。它们是由移位寄存器产生确定序列，然而他们却具有某种随机序列的随机特性。因为同样具有随机特性，无法从一个已经产生的序列的特性中判断是真随机序列还是伪随机序列，只能根据序列的产生办法来判断。伪随机序列系列具有良好的随机性和接近于白噪声的相关函数，并且有预先的可确定性和可重复性。

        所谓的随机指的相关函数是高斯的，只有自相关时为1，互相关为接近0.
        所谓的伪：指的是产生的方法是确定的，也就是这种序列是可以有确定的方法来重复产生的，而且具有周期性，而不像真正的随机序列是无法重复产生而且不具有周期性的。

        在通信从通常使用LFSR线性反馈移位寄存器来产生伪随机序列：

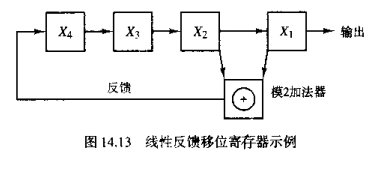
        假设初始的状态中(X4,X3,X2,X1)是1000
        现在开始移位：X1+X2 = 0， 新移入的为0， 则当前寄存器中的值为0100,输出0
        反复进行： 1000,0100,0010,1001,1100,0110,1011,0101,1010,1101,1110,1111,0111，0011,0001,1000。
        输出为: 111101011001000 （右边的最先输出)

        一维随机码：
        周期性： 理论上的最大周期为2^4 = 16, 也就是每一个寄存器都遍历过0和1两个值的数目，排列组合
               这个例子中的周期=16，经过16次移位后寄存器的值还原为初始值。
        窗口特性： 用一个较小的窗口进行滑动，得到的窗口内的序列是唯一的。这是可以推导的，从上面
               这个例子中可以看到，窗口取4正好就是寄存器在某时刻的值，肯定是唯一的。
       折叠原理： 比如一个1维的伪随机序列，可以在任何位置折叠成高维比如2维的序列仍然是伪随机的。
              比如周期为3^9 -1=19682的序列可以折叠为26x757=19682的二维伪随机序列。M-ARRAY
              折叠方法如下：

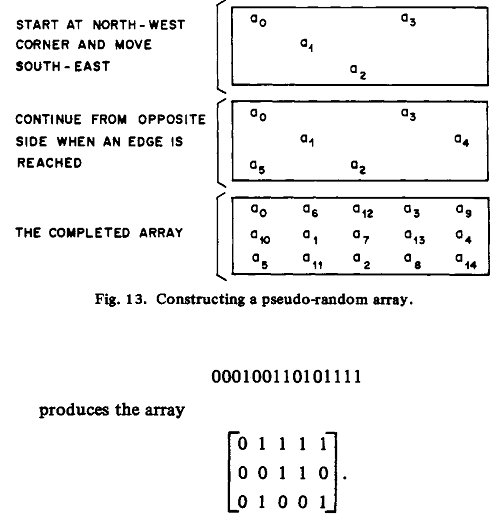
         多元域：   每一个寄存器的取值的数目，比如只能取0/1二进制，那么就是二元域，对于图像
                比如有R/G/B三个值，那么就是3元域，类推。
                下图为一个3元域的RGB的伪随机pattern：

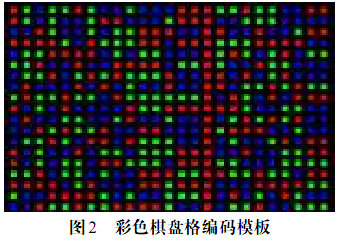
          同样的还存在二维伪随机码等：
          随机码组成一个KxL的矩阵，window size为vxw，每个window包含的码字只出现一次。
          同样具有一维伪随机码的各种特点包括窗口特性，周期性等。
   

         在结构光编码中，假设已经知道了伪随机序列的产生方法和值，那么我们就知道了下面的信息：
                 周期大小，窗口大小。

         这个已知的伪随机序列就是参考图像或者说是编码模板。

        在匹配中使用正确的窗口大小在拍摄的图片中进行滑动，对窗口中的图案进行解码，得到该窗口内的伪随机序列的片段，这个片段在已知的编码模板中搜索同样片段进行比较，如果距离为0，那么就得到了匹配点。           

       可见，这种结构光编码的方法需要预先知道编码模板，并在测试图像中正确的提取到片段信息才能正确。

       由于伪随机序列具有的窗口特性(窗口内的符号是唯一的)，因此比较适合用于结构光编码。

    后面会对结构光伪随机编码的编码实现和解码做详细的总结。

最后

以上就是受伤白羊为你收集整理的二维伪随机序列结构光编码的全部内容，希望文章能够帮你解决二维伪随机序列结构光编码所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。