论文阅读总结(七)：DeepXDE: A Deep Learning Library for Solving Differential Equations

这篇文章是关于深度学习求解偏微分方程的内容，作者对PINN(Physical Informed Neural Network)一文提出的方法进行了归纳总结，从理论层面分析了PINN解偏微分方程的可行性以及提出了改善PINN训练效率的方法，并对PINN与传统的有限元素法(FEM)进行了比较，最后作者将PINN做成了一个名为DeepXDE的python库。

PINN算法和理论分析：

深度神经网络：

深度神经网络在数学层面可以理解为一个复合函数，最简单的神经网络是前馈神经网络，本文求解偏微分方程使用的前馈神经网络和残差网络(ResNet)解决偏微分方程求解问题。

Physical Informed Neural Network

PINN的基本思想是学习一个神经网络用来拟合需要求解的偏微分方程的解析解，在训练此网络时使用偏微分方程的残差项（所有的偏导项和非线性项）对神经网络的训练进行限制。可以理解为使得神经网络在训练过程中逐渐具备了偏微分方程所描述的物理系统的先验知识。
偏微分方程的一般形式：
$$f(x;\frac{\partial u}{\partial x_1},...,\frac{\partial u}{\partial x_d};\frac{{\partial }^{2}u}{\partial x_1\partial x_1},...,\frac{{\partial }^{2}u}{\partial x_1\partial x_d};...;\lambda )$$
边界条件：
$$B(u,x)=0\mathrm{o}\mathrm{n}\partial \Omega$$
其中我们将$t$考虑为$x$中的一个维度
PINN算法流程：

1. 构建一个多层神经网络$\hat{u}(x;\theta )$
2. 指定两个数据集$T_f$,$T_b$分别代入方程和边界条件计算loss训练神经网络用。
3. 指定一个loss function：需要平衡PDE残差和边界条件残差。
4. 通过最小化loss来训练神经网络以找到最终参数${\theta }^{\ast }$。

loss function:
$$L(\theta ;T)=w_f{L}_f(\theta ;T_f)+w_b{L}_b(\theta ;T_b)$$
其中
$$L_f(\theta ;T_f)=\frac{1}{T_f}\sum _{x\in T_f}||f(x;\frac{\partial \hat{u}}{\partial x_1},...,\frac{\partial \hat{u}}{\partial x_d};\frac{{\partial }^2\hat{u}}{\partial x_1\partial x_1},...,\frac{{\partial }^2\hat{u}}{\partial x_1\partial x_d};...;\lambda )|{|}_2^2$$
$$L_b(\theta ;T_b)=\frac{1}{T_b}\sum _{x\in T_b}||B(\hat{u},x)|{|}_2^2$$
文中提到了三种取样本点的方法:
1.在训练开始前取点，开始训练后一直使用这些点不再改变。
2.每一次迭代优化都随机取不同的点。
3.在训练过程中自适应的改变残差点的位置。

PINN近似理论与误差分析：

作者通过理论分析说明只要神经网络有足够的神经元和层数，可以近似任何函数及其导数。对神经网络近似理论的理论分析感兴趣的可以参考Approximation theory of the MLP model in neural networks这篇paper。
假设对于给定的偏微分方程的最优解析解为$u$，我们设置的神经网络的可以近似的所有函数构成的函数空间为$F$, $u$很可能不在假设空间$F$, 定义：
$$u_F=\underset{f\in F}{\mathrm{argmin}}||f-u||$$
因为我们只在空间中的某个特定的数据集T上训练模型，定义：
$$u_T=\underset{f\in F}{\mathrm{argmin}}L(f;T)$$
简单来说$u_T$是固定网络结构(即参数空间)的模型在数据集T上训练可以得到的最优解，但我们知道deep learning在大多数情况都不能得到最有解，换句话说通过用数据训练模型我们只能得到次优解。定义${\tilde{u}}_T$为我们训练模型后得到的次优解，则我们的目标为最小化:
$$||{\tilde{u}}_T-u||$$
利用三角不等式可以将上式分解：
$$\begin{gathered} ||{\tilde{u}}_T-u||<=||{\tilde{u}}_T-u_T||+||u_T-u_F||+||u_F-u|| \\ ={\epsilon }_{opt}+{\epsilon }_{gen}+{\epsilon }_{app} \end{gathered}$$
其中右边第一项与训练时的迭代次数与学习率等超参数相关，第二项与训练模型选取的数据集相关，最后一项与网络的架构有关。

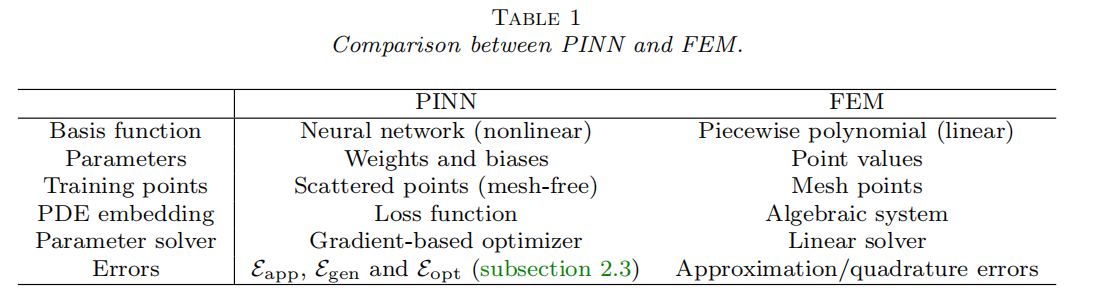
比较PINNs和FEM

PINNs解决积分微分方程

例如，当解决此类方程时：
$$\frac{dy}{dx}+y(x)={\int }_0^x{e}^{t-x}y(t)dt$$
首先使用度为n的Gaussian quadrature近似积分项：
$${\int }_0^x{e}^{t-x}y(t)dt\approx \sum _{i=1}^n{w}_i{e}^{t_i(x)-x}y(t_i(x))$$
之后使用PINNs解决下述PDE：
$$\frac{dy}{dx}+y(x)\approx \sum _{i=1}^n{w}_i{e}^{t_i(x)-x}y(t_i(x))$$

PINNs解决逆问题：

此类问题给定方程形式求解方程参数以及解析解，除了偏微分方程的残差项以及边界条件，我们在domain的边界上会有额外的信息点：
$$I(u,x)=0forx\in T_i$$
和求解PDE的问题一样简单，只不过loss function改为以下形式：
$$L(\theta ,\lambda ;T)=w_f{L}_f(\theta ,\lambda ;T_f)+w_b{L}_b(\theta ,\lambda ;T_b)+w_i{L}_i(\theta ,\lambda ;T_i)$$
$$L_i(\theta ,\lambda ;T_i)=\frac{1}{|T_i|}\sum _{x\in T_i}||I(\hat{u},x)|{|}_2^2$$
此时优化目标变为：
$${\theta }^{\ast },{\lambda }^{\ast }=\text{arg}mi{n}_{\theta ,\lambda }L(\theta ,\lambda ;T)$$

Residual-based adaptive refinement(RAR)

前面讲到训练模型时的样本点通过随机采样得到，作者指出针对一些特定的偏微分方程这样采样训练的效率不高。例如Burgers equation我们应该在梯度“很陡”的地方采样较多的样本点。但针对方程解未知的情况设计残差点的一个好的采样分布具有挑战性。
作者采用的方法的基本思想是在偏微分方程残差大的位置多取一些点。
具体算法如下：

最后

以上就是精明野狼为你收集整理的论文阅读总结(七)：DeepXDE: A Deep Learning Library for Solving Differential Equations的全部内容，希望文章能够帮你解决论文阅读总结(七)：DeepXDE: A Deep Learning Library for Solving Differential Equations所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。