matlab ceil函数_科学计算 | MATLAB基础知识

最近期末考试结束了，自己立下了一个flag，自学MATLAB，写这篇文章的目的就在于将自己所学的知识输出，希望能够帮到你。大家一起相互学习吧！话不多说，下面直接进入主题。

01matlab系统环境

1.matlab操作界面的组成

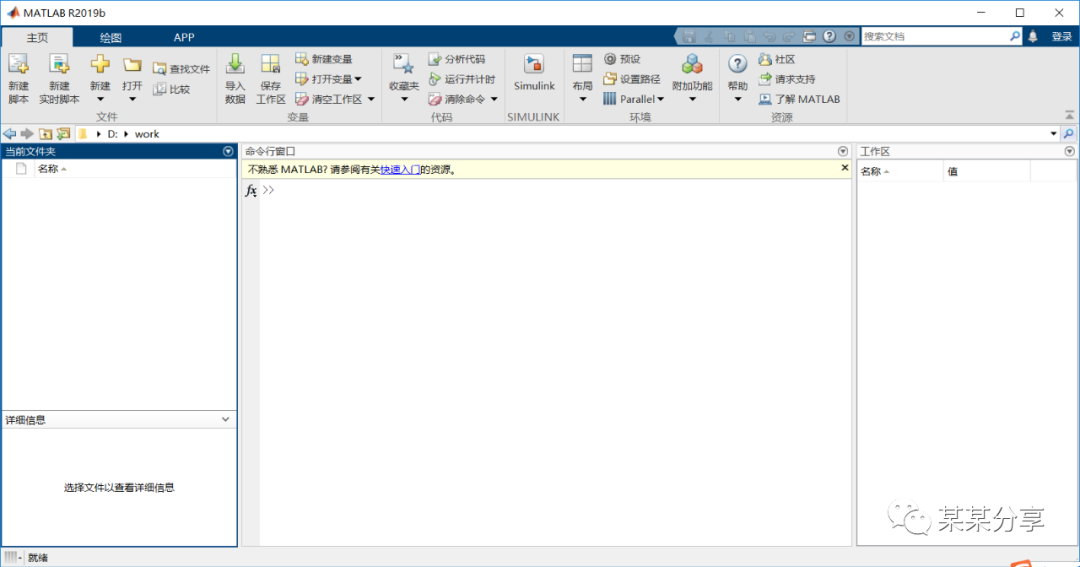
⑴matlab主窗口包括:功能区 快速访问工具栏 当前文件夹工具栏

⑵命令行窗口

用于输入命令并显示命令的执行结果

注意：当在命令行窗口执行命令时，如果不想立即在命令行窗口输出结果，可以在命令后加上分号(；)

⑶当前文件夹窗口

如何设置当前文件夹?

• 在当前文件夹工具栏或当前文件夹窗口中选择某文件夹为当前文件夹

• 使用cd命令

>> cd d:work>> cd d:work1错误使用 cd无法将目录更改为 e:work1 (名称不存在或不是目录)。

注意:一定要先建立文件夹，再将文件夹设为当前文件夹

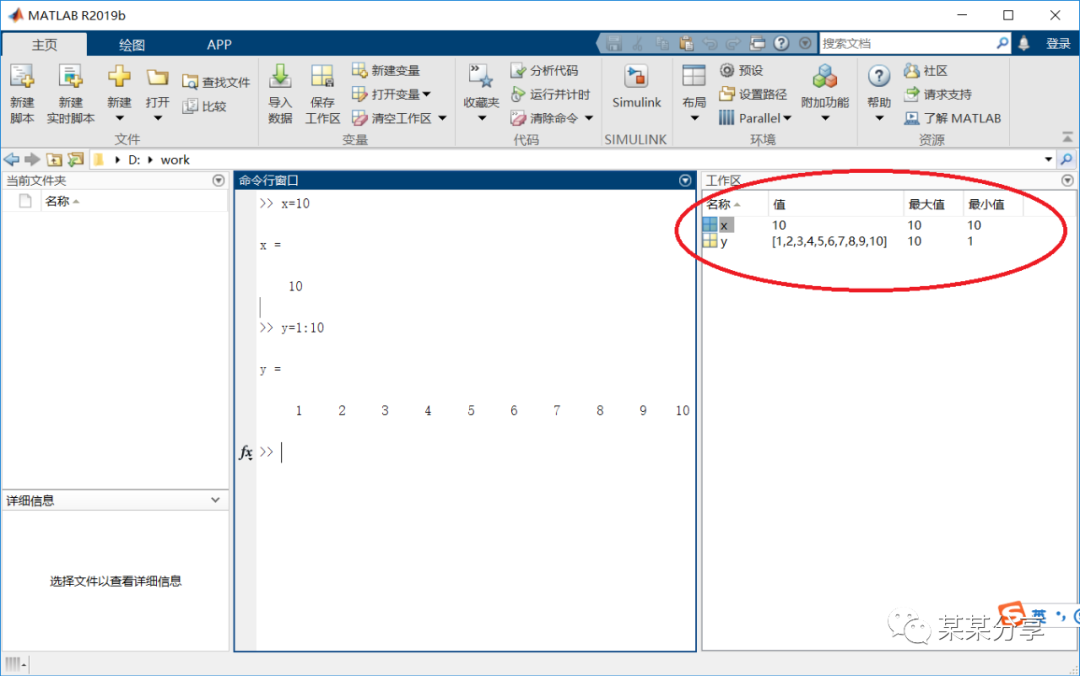
⑷工作区窗口

可以对变量进行编辑、保存和删除等操作

2.matlab的搜索路径

当用户在命令行窗口输入一条命令后，matlab将按照一定顺序依次寻找相关的命令对象

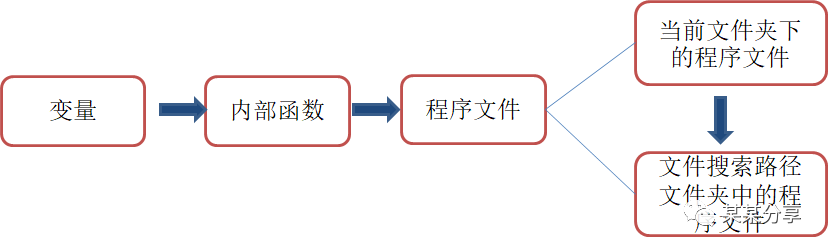
>> x=sin(1)x =    0.8415>> sin=[1,2,3,4,5]sin =     1     2     3     4     5>> sin(1)ans =     1

• 用path命令设置文件搜索路径

>> path(path,'d:work')

• 用对话框设置文件搜索路径

选择主页，再单击环境功能组中的设置路径按钮

02matlab数值数据

1.数值数据类型的分类

⑴整型

无符号8位整数数据范围:00000000-11111111(0-255)

带符号8位整数数据范围:10000000-01111111(-128-127)

unit8函数:将数值数据转换为无符号8位整数

>> x=uint8(128)x =   128

int8函数:将数值数据转换为带符号8位整数

>> x=int8(128)x =   127

⑵浮点型

single函数:将其他类型的数据转化为单精度型

double函数:将其他类型的数据转化为双精度型

>> class(4)ans =    'double'>> class(single(4))ans =    'single'

class函数：返回对象的类的名称

⑶复型

由虚部和实部两部分组成，默认为双精度，虚部单位用i或j来表示

real函数:求复数的实部

>> real(6+5i)ans =     6

imag函数:求复数的虚部

>> imag(6+5i)ans =     5

2.数值数据的输出格式

format命令

格式：format 格式符

注意:format命令只影响数据输出格式，而不影响数据的计算和存储

>> format long>> 20/3ans =   6.666666666666667>> format>> 20/3ans =    6.6667

3.常用数学函数

⑴函数的调用格式为:函数名(函数自变量的值)

• 指数函数

 A=exp(2)A =    7.3891

• 三角函数

注意：三角函数有以弧度为单位的函数和以角度为单位的函数，如果是以角度为单位的函数就在函数名后面加“d”，以示区别

>> sin(pi/2)ans =     1>> sind(90)ans =     1

• abs函数可以求实数的绝对值、复数的模、字符串的ASCII码值

>> abs(-1)ans =     1>> abs(3+4i)ans =     5>> abs('a')ans =    97

• 用于取整的函数fix、floor、ceil、round

>> fix(-4.6)          %舍去小数取整ans =    -4>> floor(-4.6)        %向下取整ans =    -5>> ceil(-4.6)         %向上取整ans =    -4>> round(-4.6)        %按照四舍五入的规则取整ans =    -5

03变量及其操作

1.变量与赋值语句

在matlab中，变量名是以字母开头，后接字母、数字或下划线的字符序列，最多63个字符。

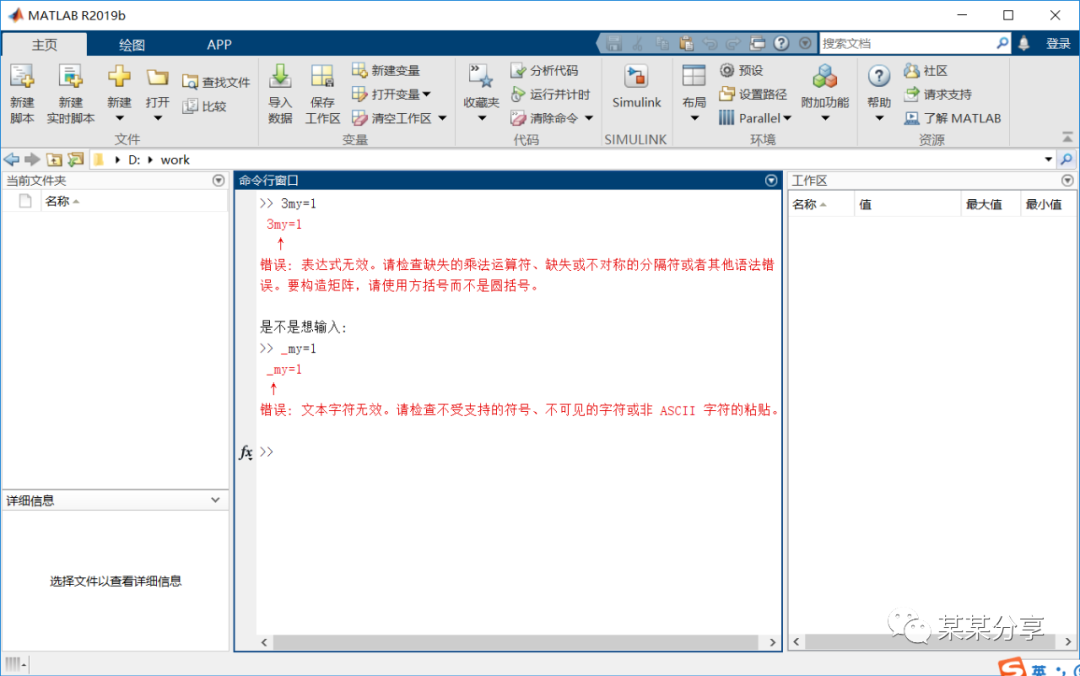
• 变量名区分字母的大小写

• 标准函数名以及命令名一般用小写字母

赋值语句两种格式：

• 变量=表达式

• 表达式

2.预定义变量

预定义变量是matlab工作空间中驻留，由系统本身定义的变量

• ans是默认赋值变量

• i和j代表虚数单位

• pi代表圆周率

• NaN代表非数(在绘图的时候，如果想裁掉其中一部分，那么只要把要裁掉的部分的坐标数据设为NaN就可以了)

3.变量的管理

⑴内存变量的删除与修改

直接在工作区进行

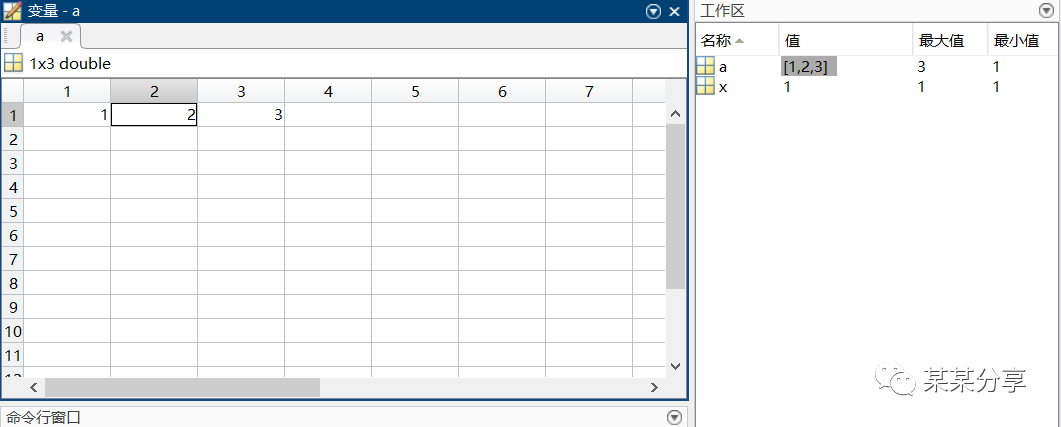
who命令与whos命令

>> x=1x =     1>> a=1:3a =     1     2     3>> who您的变量为:a  x  >> whos  Name      Size            Bytes  Class     Attributes  a         1x3                24  double                x         1x1                 8  double              

⑵内存变量文件

用于保存matlab工作区变量的文件叫做内存变量文件，其扩展名为.mat，也叫MAT文件

save命令:创建内存变量文件

load命令:装入内存变量文件

>> save madata a x>> load mydata

04matlab矩阵的表示

1.矩阵的建立

⑴直接输入法:矩阵中的元素用中括号括起来，同一行各个元素用逗号或空格分开，不同行用分号隔开

>> a=[1,2,3,;4,5,6;7,8,9]a =     1     2     3     4     5     6     7     8     9

⑵利用已建好的矩阵建立更大的矩阵

2.冒号表达式

格式：

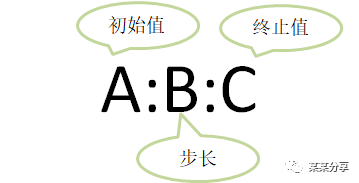
>> x=1:2:6x =     1     3     5

注意：省略步长B，则步长为1

在MATLAB中还可以用linspace函数产生行向量

格式：

3.结构矩阵和单元矩阵

⑴结构矩阵

格式:结构矩阵元素.成员名=表达式

>> a(1).x1=10;a(1).x2='liu';a(1).x3=[11,21;32,36];>> a(2).x1=12;a(2).x2='lu';a(2).x3=[1,2;52,76];>> a(3).x1=30;a(3).x2='li';a(3).x3=[31,51;72,36];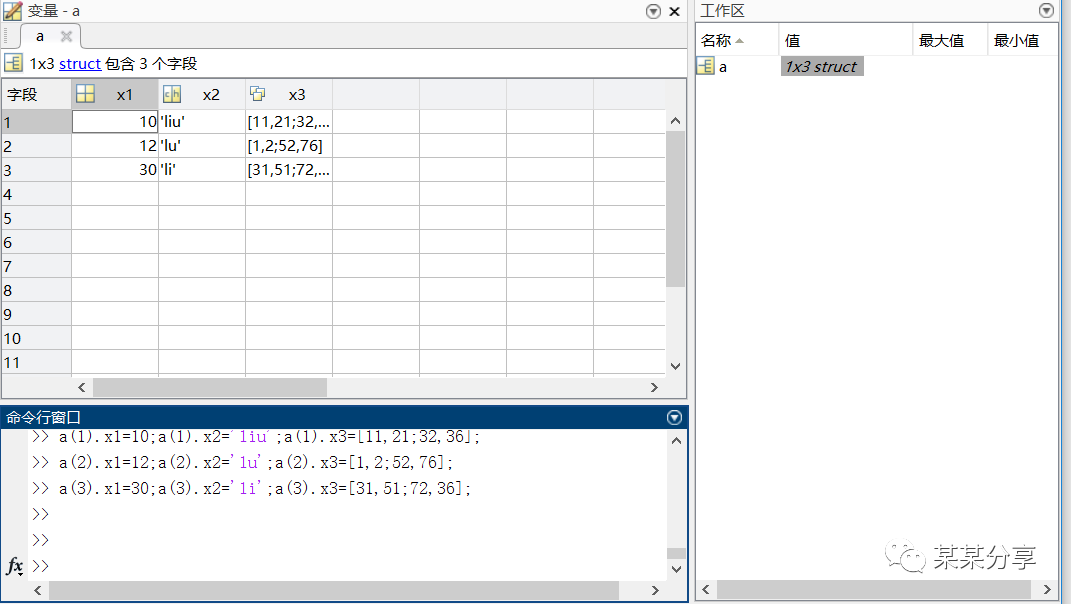

⑵单元矩阵

>>  b={10,'liu',[11,21;32,36];12,'lu',[1,2;52,76];30,'li',[31,51;72,36]}b =  3×3 cell 数组    {[10]}    {'liu'}    {2×2 double}    {[12]}    {'lu' }    {2×2 double}    {[30]}    {'li' }    {2×2 double}

单元矩阵与一般矩阵类似，直接输入即可，只是单元矩阵元素用大括号括起来

05矩阵元素的引用

1.矩阵元素的引用方式

⑴通过下标来引用矩阵的元素

A(1,1)表示A矩阵第1行第1列的元素

>> a=[1,2,3,;4,5,6;7,8,9];>> a(1,1)=10a =    10     2     3     4     5     6     7     8     9

注意：若给出的行下标或列下标大于原来的行数和列数，那么扩展后的没有赋值的矩阵元素置零

⑵通过序号来引用

在matlab中，矩阵元素按列存储

>> a=[1,2,3,;4,5,6;7,8,9];>> a(3)ans =     7

sub2ind函数：将矩阵中指定元素的行、列下标转换成存储的序号

格式：

>> A=[1:3;4:6]A =     1     2     3     4     5     6>> D=sub2ind(size(A),[1,2;2,2],[1,1;3,2])D =     1     2     6     4

ind2sub函数：将把矩阵元素的序号转换成对应的下标

格式：

>> [I,J]=ind2sub([3,2],[1,3,5])I =     1     3     2J =     1     1     2

2.利用冒号表达式获得子矩阵

子矩阵是由矩阵中的一部分元素构成的矩阵

A(i,:)                           第i行的全部元素

A(:,j)                           第j列的全部元素

A(i:i+m,k:k+m)         第i~i+m行内且在第k~k+m列中所有元素

A(i:i+m,:)                   第i~i+m行内的全部元素

>> a=[1,2,3,;4,5,6;7,8,9]a =     1     2     3     4     5     6     7     8     9>> a(1:2,:)ans =     1     2     3     4     5     6

end运算符:表示某一维的末尾元素下标

>> a=[1,2,3,;4,5,6;7,8,9];>> a(end,:)ans =     7     8     9

3.利用空矩阵删除矩阵的元素

>> x=[]x =     []  %x就是一个空矩阵

>> a=[1,2,3,;4,5,6;7,8,9]a =     1     2     3     4     5     6     7     8     9>> a(:,[1,3])=[]a =     2     5     8

4.改变矩阵的形状

reshape函数

格式:reshape(A，m，n)

在矩阵总元素保持不变的前提下，将矩阵A重新排成m*n的二维矩阵

>> a=[1,2;3,4;5,6];>> b=reshape(a,2,3)b =     1     5     4     3     2     6

A(:)：将矩阵A的每一列元素堆叠起来 成为一个列向量

>> a=[1,2;3,4;5,6];>> b=a(:)b =     1     3     5     2     4     6

06matlab基本运算

1.算术运算

⑴基本算术运算

基本算术运算符:+(加)、-(减)、*(乘)、/(右除)、(左除)、^(乘方)

• matlab的算术运算是在矩阵意义下进行的

• 单个数据的算术运算只是矩阵运算的一种特例

• 加减运算两矩阵必须同型

• 乘法运算要求A矩阵的列数与B矩阵的行数相等

• 乘方运算要求矩阵为方阵

矩阵的乘除运算，涉及到线性代数问题，不明白的可以去回顾一下

>> a=[1,2,3;4,5,6;7,8,9]a =     1     2     3     4     5     6     7     8     9>> b=[1,5,9;4,6,4;7,5,2]b =     1     5     9     4     6     4     7     5     2>> c1=a*bc1 =    30    32    23    66    80    68   102   128   113>> c2=a/bc2 =    0.3208   -0.0283    0.1132    0.6038   -0.1415    0.5660    0.8868   -0.2547    1.0189

>> a=[10,5;1,2];>> a^2ans =   105    60    12     9

⑵点运算

点运算符：.*、./、.＼和.^

• 两矩阵进行点运算是指它们的对应元素进行相关运算，要求两矩阵同型

>> a=[10,5;1,2];>> b=[3,5;12,9];>> c=a.*bc =    30    25    12    18>> d=a*bd =    90    95    27    23

⑶关系运算

关系运算符:＜、＜=、＞、＞=、==(等于)、～=(不等于)

运算规则:

• 当两个比较量是标量，直接比较两数大小。若关系成立，关系表达式结果为1，否则为0

• 若两比较量是两个同型矩阵比较是对两矩阵相同位置的元素按标量关系运算规则逐个进行，最终结果是一个与原矩阵同型的矩阵，它的元素由0、1组成

• 当参与比较的一个是标量，另一个是矩阵，则把标量与矩阵每一个元素按标量关系运算规则逐个比较，最终结果是一个与原矩阵同型的矩阵，它的元素由0、1组成

3.逻辑运算

逻辑运算符:&(与)、|(或)和～(非)

运算规则与关系运算类似

>> 3<4&6>5ans =   1

07字符串处理

1.字符串的表示

在matlab中，字符串是用单引号括起来的字符序列

>> x='college';>> x(1:3)ans =    'col'

若字符串中的字符含有单引号，则该单引号字符要用两个单引号来表示

>> 'I''m a teacher'ans =    'I'm a teacher'

字符串矩阵

>> sh=['abc';'123']sh =    'abc'    '123'

2.字符串的操作

⑴字符串的执行

格式:eval(s)   s指字符串

>> x='[pi,sin(pi),cos(pi)]';>> y=eval(x)y =    3.1416    0.0000   -1.0000

⑵字符串与数值之间的转换

• abs和double函数都可以用来获取字符串矩阵所对应的ASCII码数值矩阵

• char函数可以把ASCII码矩阵转换为字符串矩阵

>> a1='college';>> x=abs(a1)x =    99   111   108   108   101   103   10>> char(x)ans =    'college'

⑶字符串的比较

字符串的比较有两种方法:利用关系运算符或字符串比较函数

• 关系运算符比较：两个字符串里的每个字符依次按ASCII值大小逐个比较，比较结果是一个数值向量，向量元素要么是1，要么是0

>> 'awe2'>'bh25'ans =   0   1   1   0

• 字符串比较函数用于判断字符串是否相等，有四种比较方式，函数如下：

• strcmp(s1，s2):用来比较字符串s1和s2是否相等，若相等，返回结果1，否则0

• strncmp(s1，s2，n):用来比较两个字符串前n个字符是否相等，若相等，返回结果1，否则0

• strcmpi(s1，s2):在忽略字母大小前提下，比较字符串s1和s2是否相等，若相等，返回结果1，否则0

• strncmpi(s1，s2，n):在忽略字符串大小前提下，比较两个字符串前n个字符是否相等，若相等，返回结果1，否则0

>> strcmp('xd12','hb41')ans =   0>> strncmpi('xd12','hb41',1)ans =   0

⑷字符串的查找与替换

findstr(s1，s2):在两个输入参数中较长的那个参数中搜索较短的那个参数，并返回找到的每一处的起始索引。如果未找到任何字符串，则 findstr 返回空数组 []。

strrep(s1，s2，s3):将字符串s1中所有子字符串s2替换为字符串s3

>> p=findstr('this is test','is')p =     3     6>> fx=strrep('this is a test!','test','class')fx =    'this is a class!'

对于学习MATLAB，本人也还是菜鸟一枚，希望自己分享的学习心得能够帮助到大家。

最后祝大家暑期愉快！