评分 |
******大学实验报告
课程名称 生物医学信号处理
实验名称 数字信号处理基础
专业班级
姓 名 ******
学 号
实验日期
实验地点
******学年度第******学期
一、实验目的 1、掌握数字信号的频谱分析 2、熟悉数字滤波器的设计和实现 |
二、实验环境 1、硬件配置:处理器: Intel(R) Core(TM) i7-4790 CPU @3.60 GHz 安装内存: 4.00 GB 系统类型: 32位操作系统 3、软件环境:MATLAB R2014a |
三、实验内容 (包括本实验要完成的实验问题及需要的相关知识简单概述) 例2-9高密度频谱和高分辨率频谱的比较,设信号为: x(n)=cos(0.48 利用有限长序列的FFT来分析下列情况的幅度谱: (1)采集数据长度N=10,即0<=n<< span="">=9,做10点的DFT,画出幅度谱。 (2)采集数据长度N=10,但补90个0,做100点的DFT,画出幅度频谱。 (3)采集数据长度N=100,即0<=n<=9,画出幅度谱。< span=""> 例2-11选择一种合适的窗口设计一个FIR数字低通滤波器,满足下列要求:
并画出滤波器的单位脉冲响应和该滤波器的幅度响应。 例2-12最常碰到的信号处理任务是平滑数据以抑制高频噪声。求几个数据点的平均值是减弱高频噪声的一种简单的方法,这种滤波器称为平滑滤波器或中值滤波器。下面给出一段1000点的脑电数据用不同长度的数据点进行平滑,观察其滤波后的效果。 |
四、实验结果与分析 (包括实验原理、数据的准备、运行过程分析、源程序(代码)、图形图象界面等) 注:本项可以增加页数 实验原理: 在做频谱分析的时候,为了提高频域分辨率,常常要增加采样点数。如果数量略有不足,传统的方法是在数据尾部补零来解决,称为高密度频谱(The High Density Spectrum)。但是补零并不能够提高频域分辨率,我们认为填入适当的数据会更好,称为高分辨率频谱(The High Resolution Spectrum)。MATLAB中做频谱分析分函数为fft。 理想的数字滤波器有:低通、高通、带通和带阻数字滤波器。为了抑制高频噪声,常常还需要平滑数据,这种滤波器也称平滑滤波或中值滤波器。MATLAB中使用函数medfilt1。 实验步骤: >>%%%2-9 N1=10; %采集数据长度N=10 N2=10; %采集数据长度N=10 N3=100; %采集数据长度N=100 N4=200; %采集数据长度N=200 %做10点的DFT for i=1:N1 %将i从1增加到N1 x_1(i)=cos(0.48*pi*i)+cos(0.52*pi*i); %函数表达式 end f_1=fft(x_1,10); %对图像进行快速傅里叶变换 %做100点的DFT,其中90个点补零 for j=1:N2 % 将j从1增加到N2 x_2(j)=cos(0.48*pi*j)+cos(0.52*pi*j); %函数表达式 end for j=N2+1:N3 %j的取值范围是N2+1到N3 x_2(j)=0 %补零 end f_2=fft(x_2,100); %对图像进行快速傅里叶变换 %对100个点做DFT for k=1:N3 %将k从1增加到N3 x_3(k)=cos(0.48*pi*k)+cos(0.52*pi*k); %函数表达式 end f_3=fft(x_3,100); %对图像进行快速傅里叶变换 %对200个点做DFT for m=1:N4 %将i从1增加到N1 x_4(m)=cos(0.48*pi*m)+cos(0.52*pi*m); %函数表达式 end f_4=fft(x_4,200); %对图像进行快速傅里叶变换 subplot(4,2,1);stem(0:N1-1,x_1);title('x(n),0= %绘制子图,添加标题 subplot(4,2,2);stem(0:(2/N1):1,abs(f_1(1:N1/2+1))); %绘制子图 title('DFT Magnitude');xlabel('frequency in pi units') %添加标题,添加横坐标 subplot(4,2,3);stem(0:N3-1,x_2);title('x(n),0= %绘制子图,添加标题 subplot(4,2,4);stem(0:(2/N3):1,abs(f_2(1:N3/2+1))); %绘制子图,添加标题 title('DFT Magnitude');xlabel('frequency in pi units') %添加标题,添加横坐标 subplot(4,2,5);stem(0:N3-1,x_3);title('x(n),0= %绘制子图,添加标题 subplot(4,2,6);stem(0:(2/N3):1,abs(f_3(1:N3/2+1))); %绘制子图,添加标题 title('DFT Magnitude');xlabel('frequency in pi units') %添加标题,添加横坐标 subplot(4,2,7);stem(0:N4-1,x_4);title('x(n),0= %绘制子图,添加标题 subplot(4,2,8);stem(0:(2/N4):1,abs(f_4(1:N4/2+1))); %绘制子图,添加标题 title('DFT Magnitude');xlabel('frequency in pi units') %添加标题,添加横坐标
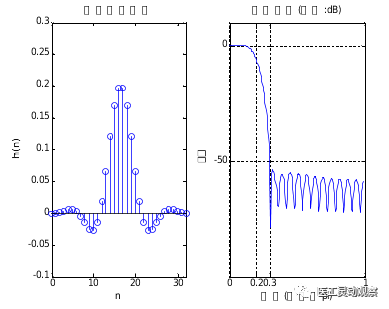
图1 三种情况下的幅度频谱 分析:图1中第一列是4种信号,第二列是对应信号的DTF幅度谱。第一行采集点数为10点,由于取的点数太少,分辨率为0.2 >> %%%2-11 wp=0.2*pi; ws=0.3*pi; %给出通带频率和阻带频率 tr_width=ws-wp; %求过渡带宽度 %因为As=50dB,hamming window即可满足该条件,查表求得窗长度 M=ceil(6.6*pi/tr_width); %取整,确定滤波器阶数,ceil是向上取整函数 n=[0:1:M-1]; %n的取值范围为0到M-1 wc=(ws+wp)/2; %求截止频率 b=fir1(M,wc/pi); %求FIR低通滤波器系数,默认就是hamming window h=b(1:end-1); %h的长度为1到end-1 [hh,w]=freqz(h,[1],'whole'); %求滤波器的频率响应 hhh=hh(1:255);ww=w(1:255); %由于对称性,画一半图即可 subplot(1,2,1);stem(n,h); %绘制子图 title('实际脉冲响应'); %添加标题 axis([0 M-1 -0.1 0.3]); %自定义坐标取值范围 xlabel('n');ylabel('h(n)'); %给横纵坐标添加标注 subplot(1,2,2);plot(ww/pi,20*log10(abs(hhh))); %绘制子图 title('频率响应(单位:dB)');grid %添加标题,绘制网格图 axis([0 1 -100 10]); %自定义坐标取值范围 xlabel('频率');ylabel('分贝'); %给横纵坐标添加标注 set(gca,'XTickmode','manual','Xtick',[0,0.2,0.3,1]) %设置横轴间距,可以在0~1间显示坐标 set(gca,'YTickmode','manual','Ytick',[-50,0]) %设置横轴间距,可以在0~1间显示坐标
图2 低通数字滤波器设计1
改变通带频率和阻带频率:
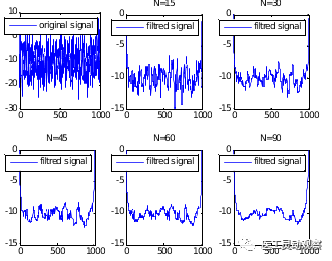
图3 低通数字滤波器设计2 分析:图2中带通频率为0.2,阻带频率为0.3 图3中带通频率为0.1 >> %%%2-12 x=-10+5*randn(1,1000); %产生均值为-10,方差为5的随机数 n=0:999; %n的取值范围是0到999 y1=medfilt1(x,15); %medfilt1为中值滤波器,对15个点取中值 y2=medfilt1(x,30); %medfilt1为中值滤波器,对30个点取中值 y3=medfilt1(x,45); %medfilt1为中值滤波器,对45个点取中值 y4=medfilt1(x,60); %medfilt1为中值滤波器,对60个点取中值 y5=medfilt1(x,90); %medfilt1为中值滤波器,对90个点取中值 subplot(2,3,1);plot(n,x);legend('original signal'); %建立子图,添加标题 subplot(2,3,2);plot(n,y1);title('N=15');legend('filtred signal'); %建立子图,添加标题 subplot(2,3,3);plot(n,y2);title('N=30');legend('filtred signal'); %建立子图,添加标题 subplot(2,3,4);plot(n,y3);title('N=45');legend('filtred signal'); %建立子图,添加标题 subplot(2,3,5);plot(n,y4);title('N=60');legend('filtred signal'); %建立子图,添加标题 subplot(2,3,6);plot(n,y5);title('N=90');legend('filtred signal'); %建立子图,添加标题
图3 平滑滤波效果图 分析:N越大,曲线越来越光滑。 思考题: 例2-9中每种情况的频域分辨率为多少?哪种情况能够反映原始信号的频域成分? 答:采集点数为10点,由于取的点数太少,2 例2-12中平滑数据点的长度N与滤波效果是什么关系? 答:N越大,曲线越来越光滑。 |
五、实验小结: (包括主要实验问题的最终结果描述、详细的收获体会,待解决的问题等) 通过本次实验,我对高密度频谱和高分辨率频谱有了更深的了解与认识,它们可以使用有限长序列FFT来分析幅度谱,采集足够的数据,幅度谱就能清楚第反映原始信号包含的频率。 FIR是有限长脉冲响应滤波器,它没有反馈回路,在设计FIR数字低通滤波时,要选择合适的窗来设计。 通过平滑滤波或中值滤波能抑制高频噪声,平滑数据点数越大,曲线就会越来越平滑。 手写签名: |
最后
以上就是自觉樱桃最近收集整理的关于频率响应函数与数字滤波实验_生物医学信号处理实验一的全部内容,更多相关频率响应函数与数字滤波实验_生物医学信号处理实验一内容请搜索靠谱客的其他文章。
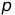 n)+cos(0.52
n)+cos(0.52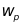 =0.2
=0.2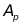 =0.25dB ,
=0.25dB , 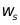 =0.3
=0.3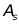 =50dB
=50dB
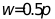 ,这个结果也和原始信号包含两个频率成分不相符。前面两种都发生了泄露现象。第三行和第四行就采集了100和200个数据,幅度谱清楚地反映了原始信号包含两个频率成分0.48
,这个结果也和原始信号包含两个频率成分不相符。前面两种都发生了泄露现象。第三行和第四行就采集了100和200个数据,幅度谱清楚地反映了原始信号包含两个频率成分0.48








发表评论 取消回复