这里总结一点matlab在微分方程中的应用,解微分方程有两种解,一种是解析解,一种是数值解,这两种分别对应不同的解法,下面就粗略的介绍一下两种解的解法。
解析解
利用dsolve函数进行求解
syms x;
s = dsolve('eq1,eq2,...', ’cond1,cond2,...', 'v');
%eq:微分方程
%cond:条件
%v:独立变量
%形如:方程:y'= f(t,y),初值:y(t0) = y01.求解析解
求
s = dsolve('D2y=3*y+2*x','x');
% D2y用以表示y的二阶导数,默认是以t为自变量的,所以最好指明自变量为x.
syms y(x);
s = dsolve([diff(y,x,2) == 3*y+2*x], [y(0) == 5])
% diff内依次是函数、自变量、微分阶数,方程用==表示相等而不是赋值2.初值问题
求初值问题
s = dsolve('Dy = y - 2*t / y','y(0) =1');3.边界问题
求边界问题
s = dsolve('x*D2y - 3*Dy =x^2','y(1)=0','y(5) = 0','x');4.高阶方程
求解方程
s=dsolve('D2y =cos(2*x) - y','y(0) =1','Dy(0) = 0','x');
simplify(s);
(eqn,cond,‘IgnoreAnalyticConstraints’,false) %设置不化简结果5.方程组问题
求解方程组
[f,g]= dsolve('Df = f + g','Dg = -f + g','f(0)=1','g(0) = 2','x'); 数值解
%龙格库塔法(Runge-Kutta法)
xfun=@(t,x)0.3.*x.*(1-x/8); %定义赋值函数r=0.3,k=8
[tout,xout]=ode45(fun,[0,40],0.1) %方程数值解,四五阶RK法
[tout,xout]=ode23(xfun,[t0,tfinal],x0) %二三阶RK法
%%
ode系列数值求解形如 / = ( , )的微分方程组, 并绘图。
xfun: 输入参数,函数必须恰有t,x两个变量,用函数文件定义的fun.m则用@fun或‘fun’调用。
t0:输入参数,t的初始值。
tfinal:输入参数,t的终值。
x0:输入参数,x的初始值。
tout: 离散的自变量值, xout: 离散的函数值。
%%同时也有一些其他的求解语句和输出语句
%%
其他的求解语句
ode45 ode113 ode15s
ode23s ode23t ode23tb
其他的输出语句
odeplot odeprint
odephas2 odephas3
%%一个例子
求
首先对该方程进行换元
然后建立m文件
function fyy=rhf(t,x)
fyy=[y(1).*(1-y(2).^2)+y(2);y(1)];
end最后计算数值解
y0=[0.25,0]’;
[t,y]=ode23(‘rhf’,[0,0.25],y0);
plot(t,y)下面介绍一些微分方程模型
微分方程模型
1.种群增长Logistic模型
-
表示在时刻
时刻种群数量
-
表示种群的内禀增长率,即在没有资源限制下的种群增长率
-
表示环境载量,反映资源环境对种群增长的制约作用
2.生物种群竞争模型
- 用
和
分别表示在时刻
甲、乙两个种群数量。
-
表示种群甲自身的被抑制的情况
-
表示种群乙对种群甲的竞争力
一个例子
考虑Lorents方程组
取参数
首先建立m文件
function dot=odone(t,y)
dot=[10*(y(2)-y(1));
28*y(1)-y(2)-y(1)*y(3);
y(1)*y(2)-(8/3)*y(3)];
end其次主程序为
[tt,yy]=ode45(@odone,[0,200],[1;2;3]);
plot3(yy(:,1),yy(:,2),yy(:,3));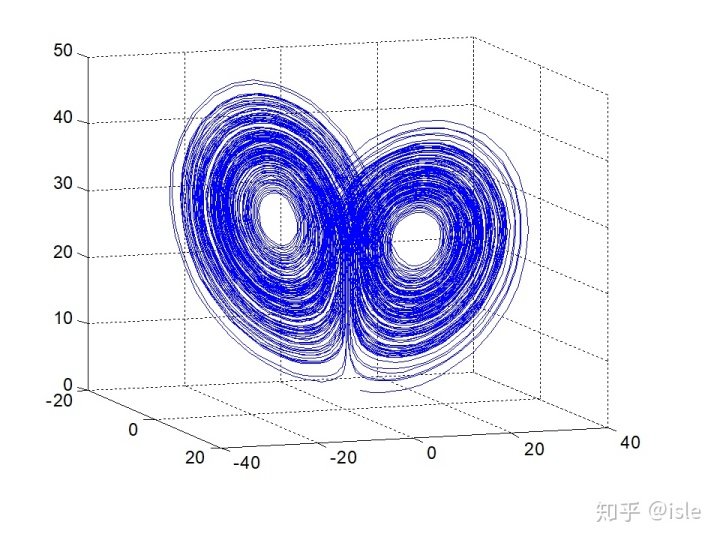
最后
以上就是过时店员最近收集整理的关于阻滞增长模型求解_浅谈用Matlab求解微分方程的全部内容,更多相关阻滞增长模型求解_浅谈用Matlab求解微分方程内容请搜索靠谱客的其他文章。
本图文内容来源于网友提供,作为学习参考使用,或来自网络收集整理,版权属于原作者所有。








发表评论 取消回复