arma模型_时间序列分析第06讲（MA(2)例子，ARMA模型）

（5）特殊的 MA 序列

考察模型

其自协方差函数是 1 步截尾的，所以它是 MA(1) 序列。

因此存在

为了求 b 以及白噪声方差，我们计算新模型的自协方差函数得到

由此可得

将 b 回代可得白噪声方差为

从 b 的解有两个能够看出，如果我们不施加最小相位条件，那么得到的模型表示可能不唯一。

（6）MA(2) 序列

对于可逆的 MA(2) 序列

满足特征多项式的根不在单位圆内，即

那么系数的取值范围是

这里利用 AR(2) 序列的稳定域的结论，令其中的 a1=-b1, a2=-b2 即得该范围。这个范围也称为 MA(2) 序列的可逆域。

其自协方差函数为

自相关系数为

谱密度为

3.2 自回归滑动平均 ARMA 模型

主要介绍四个内容并介绍一些例子：

• 模型定义及平稳解
• 自协方差函数
• 可识别性
• 谱密度和可逆性

（一）ARMA 模型

设

无公共根（否则模型可简化），且满足 最小相位条件（为了模型的唯一性）

称

为自回归滑动平均模型，简称 ARMA(p,q) 模型。其平稳序列称为 ARMA(p,q) 序列。

为了求平稳解，先介绍一个引理（实际上 AR 序列部分已经介绍）

引理 设实系数多项式

且对有界数列

（二）ARMA 模型平稳解

将模型记为

因为级数收敛，所以系数是负指数趋于 0 的（这里的系数

wold系数），同时作用

是线性平稳列（因为是白噪声的组合且系数负指数趋于0）并且是差分方程的平稳解。

唯一性：如果有另外一个解 Yt 也满足差分方程，那么

所以上面推导得到的是差分方程的唯一平稳解。

（三）ARMA 模型方程通解

模型的任意解具有以下形式

即 特解+齐次差分方程通解，这里的齐次差分方程就是

说明：齐次差分方程通解当 t 很大的时候，是趋于 0 的，不影响差分方程的平稳解。所以模拟的时候，只要去掉前面的 m 项就可以了，当 A(z) 的根靠近单位圆时，m 要取大一点。一般来说去掉前 100 项就基本没问题了。

（四）ARMA 序列自协方差函数

根据线性序列的自协方差函数公式，有

其中 wold 系数 是负指数趋于 0 的，因此自协方差函数也是负指数趋于 0.（推导在第 01 讲：系数绝对可和，那么自协方差函数趋于 0）

（五）wold 系数递推式

可以看出，自协方差函数中有 wold 系数，而根据定义 wold 系数是由级数展开得到的，为了便于编程，给出下面的递推式

其中 bj 和 ak 为 ARMA 模型中的参数，并记

推导：利用定义，比较系数。

记

其中第四个等号利用 wold 系数下标非负。因此

（六）可识别性

此处将证明：ARMA 模型的自协方差函数与模型参数可以相互导出。

为了后续反证法需要，先介绍以下引理。

引理 如果 Xt 是 ARMA(p,q) 序列，且有实系数多项式

那么多项式 C 的阶数不小于 p，D 的阶数不小于 q。

直观上看引理说明的是： 之前介绍的 ARMA 模型是最简单的。

（1）ARMA 序列的 Y-W 方程

前面我们求得了平稳解：

根据这个解的形式可知

即当前时点与未来的白噪声不相关。

由差分方程

两边同乘

即

先讨论 q<k 情形，此时

这和 AR 序列很像，AR 序列是取 q = 0.

事实上对于 q<k, q=k, q>k分别有

q=k 时，右边只保留

对于 k > q，该方程可写为如下矩阵形式

这里写 p 个方程是因为我们需要解

小tips：如果要编程，这个系数矩阵可以表示为

只要系数矩阵可逆，那么就可以解出

现在解得了 AR 部分的系数，令

那么 Y 是 MA(q) 序列（自协方差 q 步截尾），其自协方差函数为

前面介绍过，可以由 MA 序列的自协方差函数导出系数以及白噪声方差。到此就完成了由 ARMA 模型自协方差函数导出参数的工作。

（2）系数矩阵正定（会证！）

定理 当 m≥p 时，

反证：设

记（用向量写会方便）

那么就有

现在要证明上式对所有非负整数 k 都成立。

想象一下，如果系数矩阵下面添加了一行

根据 Y-W 方程中 k>q 情形，添加的这一行中每个分量都可以由原有矩阵中的列上的前 p 个元素线性表出，并且表出的系数是一样的（都是

递推可知对任意 k≥0 有

令

进而

可知 Yt 的自协方差函数是 q-1 步截尾的，所以它为 MA(q-1) 序列。因此存在白噪声

注意到右边推移算子对应的多项式只有 q-1 阶，与引理矛盾。

（七）ARMA 模型的一个充分条件

假设零均值平稳序列 Xt 有自协方差函数，

则 Xt 为 ARMA(p',q') 模型，其中 p'≤p, q'≤q。

证明：

先引入

再计算 Yt 的自协方差函数如下

自协方差 q 后截尾，Yt 是 MA(q) 序列。所以存在多项式 B 满足最小相位条件，且

如果 A,B 没有公共根，则上述模型为 ARMA(p,q)，否则设公因子为 C(z)（C当然也满足最小相位条件），则

模型可写为

两边同乘

（八）有理谱密度

ARMA 序列自协方差函数绝对可和，其谱密度函数计算如下

最后一个等号利用

形如这样的谱密度，称为有理谱密度。

（九）可逆的 ARMA 模型

如果进一步要求 B(z) 在单位圆上无根，则原 ARMA 模型变为可逆的 ARMA 模型。

对于可逆的 ARMA 模型，可以对

继而

表明可逆 ARMA 序列和它的白噪声序列可以相互线性表出。

例一

给定 ARMA(4,2) 模型，参数为

则 A(z) 的根为

谱密度函数图像如下

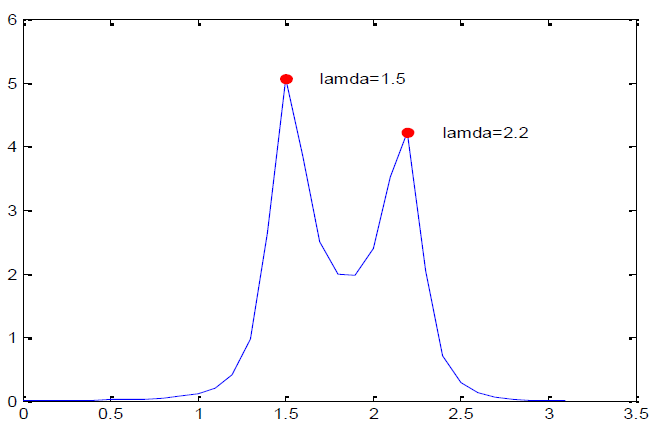
自协方差函数如下

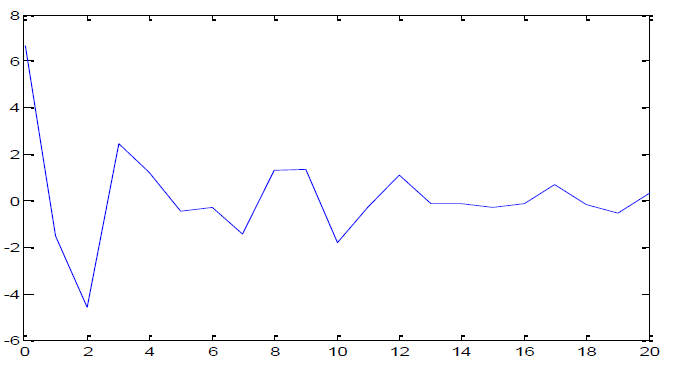
例二

已知 ARMA(2,2) 的自协方差函数为

反解其参数。

（1）根据延伸 Y-W 方程解 a1,a2

得到

（2）引进 Y 序列，并计算其自协方差

设

得到

（3）根据自协方差，利用公式求 b1,b2

其中

计算得到

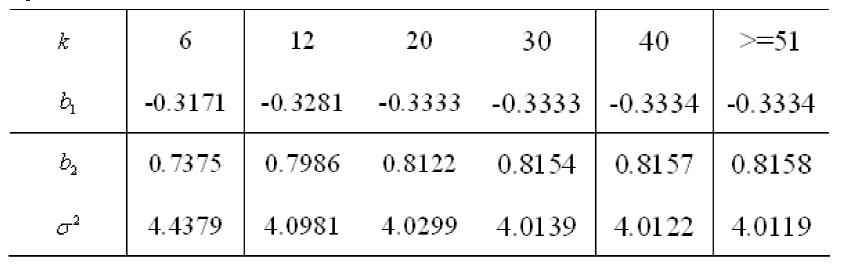
（4）得到所要的模型

其中白噪声为

推广的 ARMA 模型

如果定义中的最小相位条件去掉，就成了广义的 ARMA 模型。

如果此时 A(z) 在单位圆上有根，则不存在平稳解。

如果此时 A(z) 在单位圆上没有根，则有唯一平稳解。

这一部分下一讲再具体说明。