arma模型_回归模型算法研究——ARMA模型建模

ARMA模型建模

ARMA模型的建模过程主要包括序列平稳性检验、模型识别、参数估计、模型定阶、模型诊断与检验五个步骤，具体如下。

（1）序列平稳性检验

随机时间序列的平稳性通常是指弱平稳，其定义为：对于时间序列yt,如果其期望、方差以及自协方差均不随时间t变化，则称yt为弱平稳随机变量，即：yt必须满足以下条件：

基于随机时间序列的平稳性假设，ARMA模型在建模之前必须针对时间序列进行平稳性检验，常用方法有以下三种：

1. 过绘制时间序列的时序图进行判断。平稳时间序列中各个点的取值在其均值附近来回波动，而非平稳时间序列的均值是随着时间变化的，这种判断最为直观，但也相对粗糙。也可以通过时序图上面的数字特征（均值和方差等）进行判断。

利用样本的自相关函数（进行判断。若随着时间的增大迅速衰减，就认为是平稳序列；若是非常缓慢的衰减，则认为是非平稳序列。这种方法主要依据个人的学习经验判断，有时候不易区分，具有一定缺陷。

用统计量检验进行判断。最常用的是单位根检验（Unit Root Test），其中包括DF检验（Dickey-Fuller Test）、ADF检验（Augmented Dickey-Fuller Test等方法。这些方法对于序列的平稳性都有具体客观的判定规则，因此相比前两种方法更为准确。本文在ARMA模型建模过程中也选择该方法对随机时间序列进行平稳性检验。

在实际应用中，应根据时间序列的数据特征、选用的参数估计方法以及研究目的等选择恰当的判断方法。

(2) 模型识别

ARMA模型的识别主要是针对时间序列的相关性进行分析，具体表现为自相关函数（ACF）和偏相关函数（PACF）。

自相关函数（ACF）定义如下：

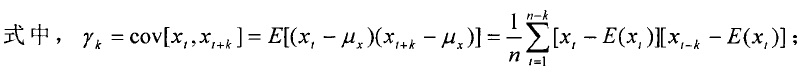
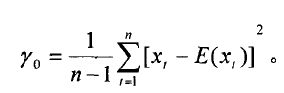
偏自相关函数（PACF）是ARMA模型的另一个重要统计特征，其定义如下：

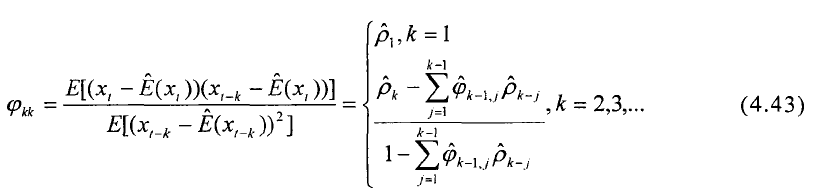
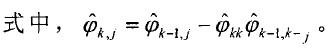
1. 若自相关函数“拖尾”，而偏相关函数在P阶后“截尾”，则可以确定为自回归模型AR(p)；
2. 若自相关函数在q阶后“截尾”，而偏相关函数“拖尾”，则可以确定为滑动平均模型MA（q）；
3. 若自相关函数和偏相关函数都“拖尾”，且分别在q阶和p阶后开始逐渐趋

于零，则可以确定为自回归滑动平均模型ARMA(p,q)。

(3) 参数估计和模型定阶

进行ARMA模型的结构及其性能分析，都是建立在模型参数和阶数己经确定的基础上。但实际上在识别和建立模型之前，对于一些已有的时间序列原始数据，通常不能确定它们是否完全符合线性关系，也难以简单按照机理方法建立模型。因此，必须采用一种可行的模型估计方法，利用有限参数尽可能逼真的描述时间序列。ARMA建模的含义包括两个方面：一是参数数量的确定，二是各参数的取值，分别称之为模型的定阶和参数估计。

目前常用的参数估计方法主要有矩估计法、极大似然估计法和最小二乘估计法等。其中，矩估计法仅适用于低阶的模型估计，而相对极大似然法的估计精度较低，且计算量非常大。最小二乘法的基本原理相对成熟，计算量小且估计精度较高，因此本文选择最小二乘法进行ARMA模型的参数估计。

对于ARMA模型的阶数P和q,常用的定阶方法有偏相关定阶法、白度检验定阶法、F检验定阶法、准则定阶法和信息熵定阶法等。前三种方法都是以假设检验方法定阶存在置信度（或置信区间）为主观因素；准则定阶法则是采用预先给定的最佳准则来确定模型阶数，其中的AIC准则是利用似然函数估计值最大原则来确定模型阶数，概念清晰，且不存在置信度的主观因素，精度较高。因此本文选择AIC准则来确定ARMA模型的阶数。

(4) 模型诊断与检验

ARMA模型建立完成后，还需对其进行诊断和检验，主要包括以下内容：

1. 平稳可逆性检验。要求方程

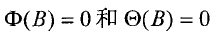
的根均在单位圆外，即根的

模均大于1。如果平稳可逆性检验未通过，可适当调整差分阶数进行修正。

②残差序列检验。模型检验的主要目的是检验模型对时间序列的拟和效果，

就是检验模型对信息的提取是否充分，即检验残差序列是否为白噪声序列。如果

拟合模型不能通过检验，即残差序列不是白噪声序列，那就要重新选择模型进行

拟合；如果残差序列是白噪声序列，则认为拟合模型是有效的。

③过拟合检验。该过程可以删掉模型中的多余参数，同时也可以尝试提高模

型的阶数，通过考察残差的平方和有无明显减小，从而判断当前所建模型是否参

数不足。

（5）ARMA模型建模流程

基于上述分析，模型的建模步骤可总结如下：

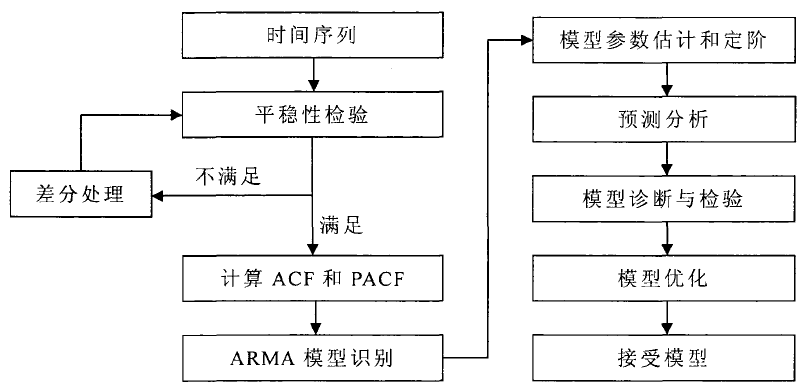
图4.2 ARMA模型建模流程

《来源于科技文献，经本人分析整理，以技术会友，广交天下朋友》