前言
电力系统外语课布置一个短期负荷预测(Load Forecasting)的project,新西兰75个月的电力负荷数据预测之后三天的电力负荷。看了给的参考文献后,我选了时间序列法,时间序列法主要有自回归AR( p),滑动平均MA(q)和自回归与滑动平均ARMA (p,q)等。这里采用ARMA,这是AR与MA结合的产物。
时间序列
一个随时间变化的值y(t),构成了一个时间序列。对于任意两段不相交的子序列,他们的统计特性如果是基本一样的,可以直观判定这个时间序列是稳定的时间序列。如果不是稳定的,需要进行预处理,比如一次差分,二次差分。
下图是建模思路:
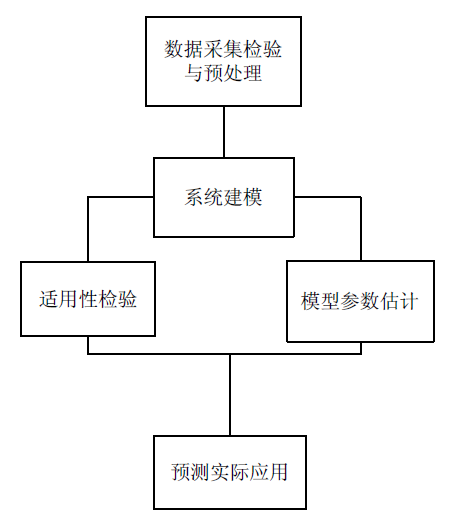
电力系统负荷预测建模流程
- 数据预处理:一次差分等,将数据处理成稳定时间序列;
- 合理选择阶数(p,q):对于预测模型的适用性检验,常采用残差方差图、最小信息准则、AIC 准则和利用自相关系数与偏自相关系数的拖尾或截尾等方法。这里使用AIC&.BIC准则,因为MATLAB中有专门的函数去计算aic和bic,选取原则是使aic和bic最小的(p,q)组合;
- 参数估计:对于预测模型的参数估计,常采用极大似然估计、矩估计和最小二乘估计等方法,这里MATLAB有直接的函数去估计相应的参数,采用的原理是极大似然估计(Maximum Likelihood Estimate,MLE)。
- 计算:得到参数后,计算之后三天的负荷量。
- 具体实施:这里将数据分成了24份,相同时间的数据一组,就是用前1092天的第n小时的数据,去预测之后三天第n小时的数据,出来的结果可能比较准确。
MATLAB程序
定阶
clear,clc;
z = importdata('C:UsersZDesktopvvv.txt');
row1 = zeros(24,1);
row2 = zeros(24,1);
for k = 1:24 %24个数据组分别计算
x = z(:,k);
y = diff(x); %消除趋势性的差分运算
logl = zeros(10,1);
PQ = zeros(10,1);
for p = 1:10 %p的个数从1取到10,计算使得相应aic和bic最小的p的个数
mod = arima('ARLags',1:p); %构造AR模型,滞后p个单位
[fit,~,logl(p)] = estimate(mod,y,'display','off'); % 估计参数
PQ(p) = p;
end
[aic,bic] = aicbic(logl,PQ+1,1901); %计算aic和bic的值
mm = min(min(bic));
nn = min(min(aic));
[row1(k),column1] = find(bic == mm); %bic最小的p值
[row2(k),column2] = find(aic == nn); %aic最小的p值
end
同理可计算q值。
计算出的结果如下:
p = [8 5 5 5 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 8 8 8 8];
q = [3 3 3 3 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 7 3];
预测
z = importdata('C:UsersZDesktopvvv.txt'); %已知数据读取
p = importdata('C:UsersZDesktopccc.txt'); % p 的个数读取
q = importdata('C:UsersZDesktopddd.txt'); % q 的个数读取
xx = zeros(3,24);
for k = 1:24 %分24组进行预测
x = z(:,k);
y = diff(x); %每组进行差分处理
n = 3; % 每组需要预测的数据数
m1 = 1092; %每组数据量
ToEstMd = arima('ARLags',1:p(k),'MALags',1:p(k),'Constant',0);%指定模型的结构
[EstMd,EstParamCov,LogL,info] = estimate(ToEstMd,y);%模型拟合
w_Forecast = forecast(EstMd,n,'Y0',y); %预测函数
yhat = y(end) + cumsum(w_Forecast); %一阶差分的还原值
for j = 1:n
x(m1 + j) = yhat(j) + x(m1+j-1); %x的预测值
xx(j,k) = x(m1 + j);
end
end
结果分析
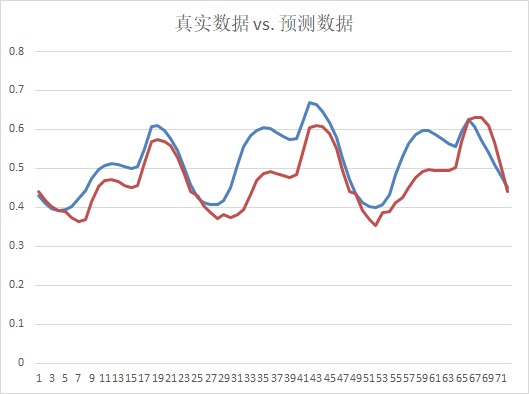
可以看到数据的基本趋势是差不多的,对此我已经很满意了,可以交作业就行了。。。
计算误差error
- 下面计算一下两组数据之间的二范数:
error = |a - b| = sqrt (sum[ (ai - bi)² ]) = 0.558; - 另一种表示误差error的形式是72个数据之间的平均误差
error = sum(| ai - bi |)/72 = 0.05332;
参考资料
MATLAB官方给的阶数确定方法
https://ww2.mathworks.cn/help/econ/choose-arma-lags.html?s_tid=srchtitlehooseARMALagsUsingBICExample-1
estimate函数的讲解
https://ww2.mathworks.cn/help/econ/arima.estimate.html?searchHighlight=estimate&s_tid=doc_srchtitle
最后
以上就是活力小蝴蝶最近收集整理的关于用MATLAB进行基于ARMA方法的负荷预测(Load Forecasting with ARMA by MATLAB)前言时间序列MATLAB程序结果分析参考资料的全部内容,更多相关用MATLAB进行基于ARMA方法的负荷预测(Load内容请搜索靠谱客的其他文章。








发表评论 取消回复