三点定位_三点定位法确定动点大致轨迹2019年武汉中考第9题

中考数学试题是检测学生学习能力，承载考试选拔功能，体现教学导向，是我们实施教学的良好素材。作为一线数学教师的我们，应该深入研究各地的中考题，追根溯源，对常见的数学问题进行深入思考。

今天探讨的问题是2019年武汉中考第9题。

如图，AB是⊙O的直径，M、N是弧AB(异于A、B)上两点，C是弧MN上一动点，∠ACB的角平分线交⊙O于点D，∠BAC的平分线交CD于点E．当点C从点M运动到点N时，则C、E两点的运动路径长的比是()

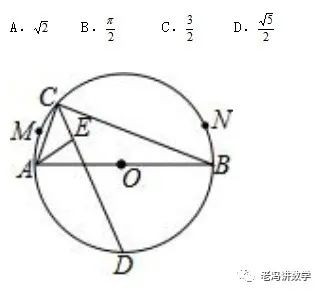
学生在考场上怎么才能“凭空”想得到点E的轨迹呢？如果想不到点E的轨迹，那就不可能去求这两个路径之比！难啊！

首先我们让这个图动起来。

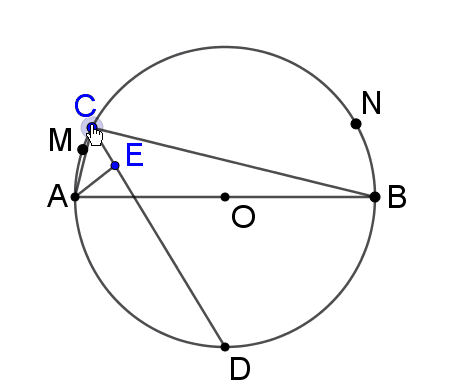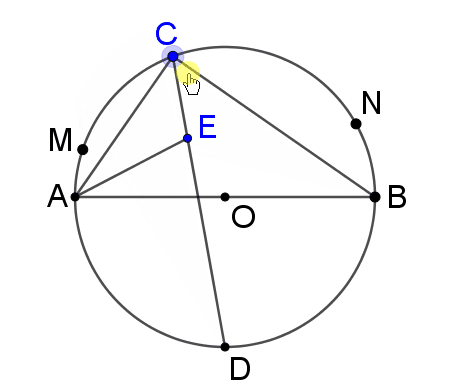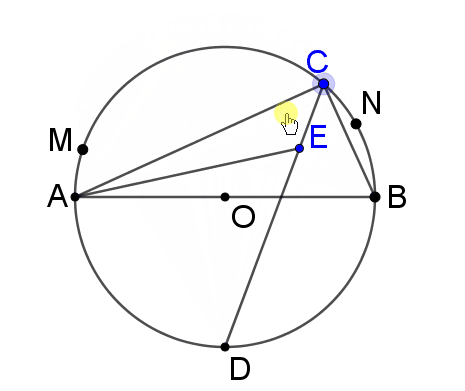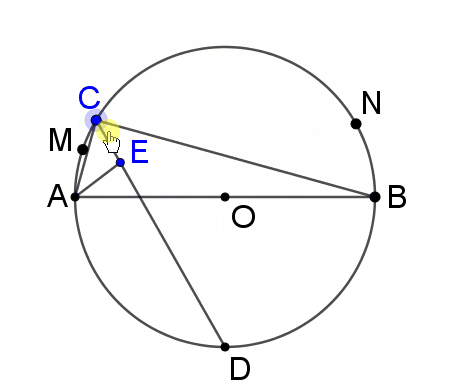
我们发现点E的运动路径好象是一个圆弧。但考场上面学生不能用电子设备啊，这里我给大家推荐“三点定位法”

初中阶段对运动路径的考查仅限于直线和圆弧。那么使用“三点定位法”就恰如其分。一般我们选取主动点的起始位置、终止位置，再加一个中间位置。学生可以通过作图进行大致判断，然后再从理论上给予必要的证明。

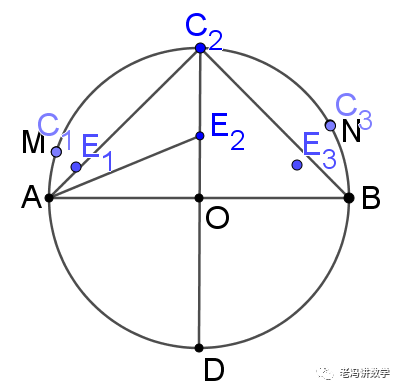
显然我们得到的三个点E不在一条直线上，所以那么点E的运动轨迹只能是圆弧。

下面我们就来进行相应的证明。

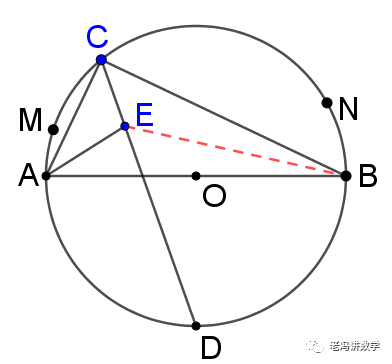
解析：连结BE，

因为点E是∠ACB与∠CAB的交点，

所以，点E是三角形ABC的内心，

所以，BE平分∠ABC，

因为AB为直径，所以，∠ACB＝90°，

所以，∠AEB＝180°－(∠CAB+∠CBA)＝135°，为定值，

那到这个位置那么就豁然开朗了，这不就是我们以前一直说的定边定角模型嘛。

所以，点E的轨迹是弓形AB上的圆弧。

再通过简单的尺规作图，我们发现过A、B、C三点的圆的圆心似乎应该是点D。

下面就是要证明DA=DE=DB。

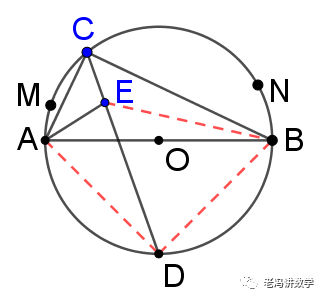
 连接AD、BD。

由题可知：

∠ACD＝∠DAB＝45°，

又∠CAE＝∠BAE

∴∠ACD+∠CAE＝∠DAB+∠BAE

即∠DEA＝∠DAE

∴DA=DE。

∵CD平分∠ACB 

∴DA=DB

∴DA=DB=DC

所以点E在以点D为圆心，以DA为半径的一段圆弧上。如图示。

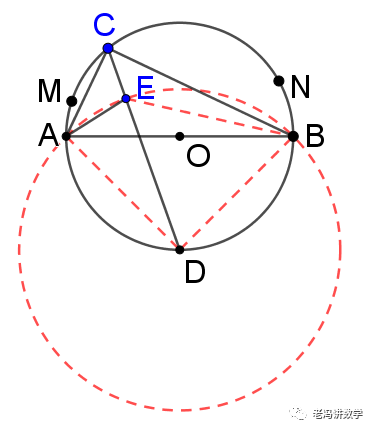
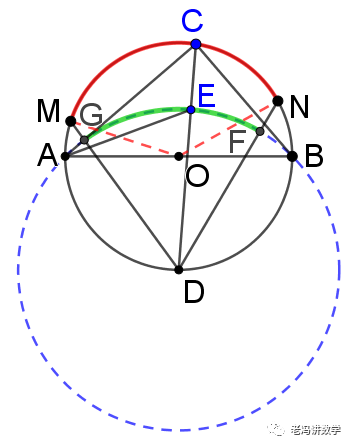
反思1：以后凡是类似的动点轨迹问题，第一步往往要求出动点的轨迹类型，这个可以利用“三点定位法”先进行一个大致的判断，再利用定边定角模型进行证明。

谢谢大家的阅读，有问题或心得体会的欢迎大家在留言处探讨……

 如果你觉得这篇文章对你的学习有帮助，欢迎转发给你的同学或老师，谢谢。

积极反思，提升能力，

分享知识，收获快乐！

敬请关注微信公众号：

老冯讲数学

予人玫瑰，手有余香。  

右下角请点击“在看”。