已知先序与中序遍历结果构建二叉树(C++版)

还原思想：

例1：先序序列：ABDGCEF 中序序列：DGBAECF,构造二叉树。

先序序列第一个为A，则根结点第一个为A，然后根据中序序列，DGB在A的左子树，ECF在A的右子树。
先序序列第二个为B（B在A的左子树上），则A左边连B，根据中序序列知道以B为根结点，DG为左子树，右子树空。
先序序列第三个为D(D在B的左子树)，则B左边连D,根据中序序列知道以D为根结点，G为右子树，左子树为空。以此类推……
图解：

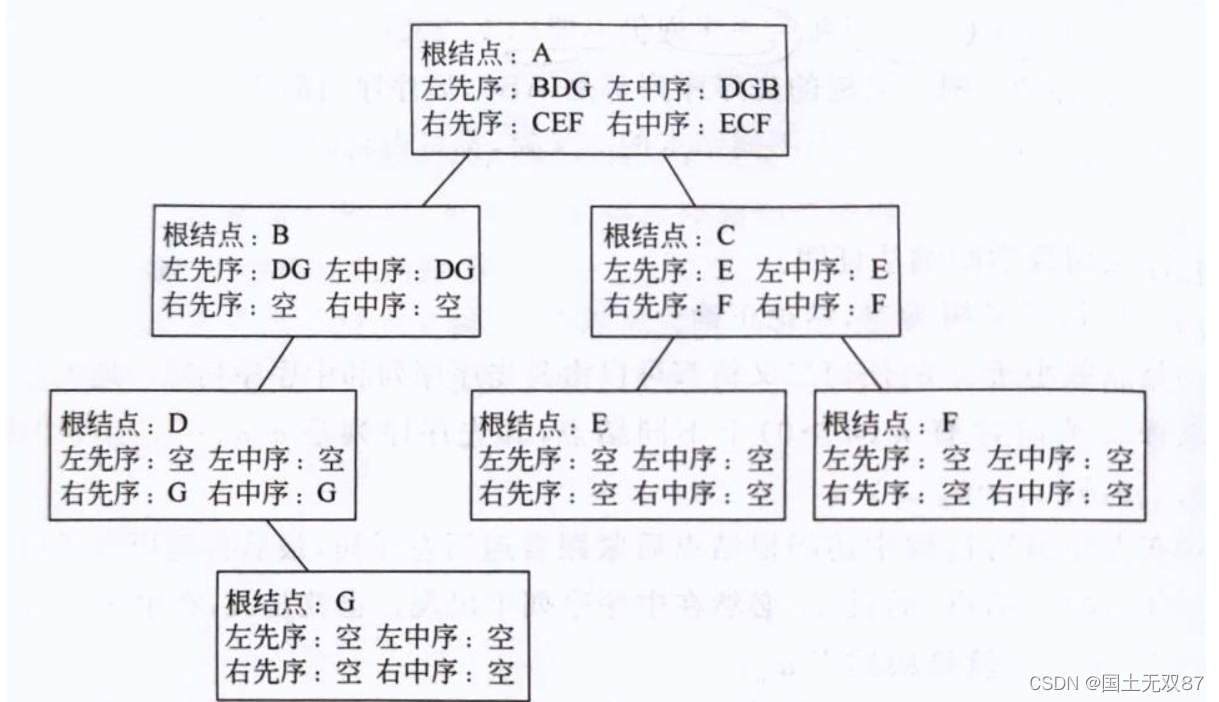
 这幅图的重点在于找左先序，左中序，右先序，右中序，我看了很多博客，这篇博客的思想较通俗易懂，用来实现代码也是较好理解。

#include<iostream>
#define MaxSize 100
using namespace std;
typedef char ElementType;

typedef struct BiTNode {
	ElementType data;
	struct BiTNode *lchild,*rchild;
}BinTNode,*BinTree;



BinTree create_BinTree(char a[],char b[],int size) //与该节点相关的先序，与该节点相关的中序,序列中的节点个数大小
{
	char c = a[0];    //记录此时根节点

	if (c == '')
	{
		return NULL;
	}
	else
	{

		int record_index=0;
		int count1 = 0, count2 = 0;
		char* new_left_PreOrder = (char*)calloc(size, sizeof(char));
		char* new_left_InOrder = (char*)calloc(size, sizeof(char));
		char* new_right_PreOrder = (char*)calloc(size, sizeof(char));
		char* new_right_InOrder = (char*)calloc(size, sizeof(char));

		for (int i = 0; i < size; i++) //寻找此时根节点在中序中的位置
		{
			if (b[i] == c)
			{
				record_index = i;
			}
		}


		for (int i = 0; i < size; i++)  //构建新的左中序，右中序
		{
			if (i < record_index)
			{
				new_left_InOrder[count1++] = b[i];
			}
			if (i > record_index)
			{
				new_right_InOrder[count2++] = b[i];
			}
		}

		count1 = 0;
		count2 = 0;

		for (int i = 1; i < size; i++)  //构建新的左先序，右先序
		{
			if (count1 < strlen(new_left_InOrder))
			{
				new_left_PreOrder[count1++] = a[i];
			}
			else
			{
				new_right_PreOrder[count2++] = a[i];
			}
		}


		BinTree Node = (BinTree)malloc(sizeof(BinTNode));
		Node->data = c;
		Node->lchild = create_BinTree(new_left_PreOrder, new_right_InOrder, count1);
		Node->rchild = create_BinTree(new_right_PreOrder, new_right_InOrder, count2);
		return Node;

	}
}


typedef struct {
	BinTree Data[MaxSize];
	int front, rear;
}Queue;

void InitQueue(Queue& Q)
{
	Q.front = Q.rear = 0;
}

bool IsEmpty(Queue& Q)
{
	if (Q.rear == Q.front)
	{
		return true;
	}
	else
	{
		return false;
	}
}

void EnQueue(Queue& Q, BinTree T)
{
	Q.Data[Q.rear] = T;
	Q.rear = (Q.rear + 1) % MaxSize;
}

bool DeQueue(Queue& Q, BinTree& p)
{
	if (IsEmpty(Q))
	{
		return false;
	}
	else
	{
		printf("%c", Q.Data[Q.front]->data);
		p = Q.Data[Q.front];
		Q.front = (Q.front + 1) % MaxSize;
		return true;

	}
}


void LevelOrder(BinTree Tree)
{
	Queue Q;
	BinTree p = (BinTree)malloc(sizeof(BinTNode));
	InitQueue(Q);
	EnQueue(Q, Tree);
	while (!IsEmpty(Q))
	{
		DeQueue(Q, p);
		if (p->lchild != NULL)
		{
			EnQueue(Q, p->lchild);
		}
		if (p->rchild != NULL)
		{
			EnQueue(Q, p->rchild);
		}
	}
}


int main()
{
	char a[] = "ABDGCEF"; //先序遍历
	char b[] = "DGBAECF";//中序遍历
	BinTree root = (BinTree)malloc(sizeof(BinTNode));
	root=create_BinTree(a, b,strlen(b));
	printf("层序遍历的结果是：");
	LevelOrder(root);


}

 结果如图：

了解构造先序与后序之后的精简代码如下，改变了参数，时间复杂度大大降低，唯一的循环仅在循环中序中发生：

#include<iostream>
using namespace std;
typedef char ElementType;

typedef struct BiTNode {
	ElementType data;
	struct BiTNode *lchild,*rchild;
}BinTNode,*BinTree;


BinTree create_BinTree(ElementType pre[],ElementType In[],int pre_index_start,int pre_index_end,int In_index_start,int In_index_end)
{
	if (pre_index_start>pre_index_end)
	{
		return NULL;
	}
	else
	{
		char c = pre[pre_index_start];    //记录此时根节点
		int record_index=0;

		for (int i = In_index_start; i <= In_index_end; i++) //寻找此时根节点在中序中的位置
		{
			if (In[i] == c)
			{
				record_index = i;
			}
		}


		BinTree Node = (BinTree)malloc(sizeof(BinTNode));
		Node->data = c;
		Node->lchild = create_BinTree(pre,In,pre_index_start+1,pre_index_start+(record_index-In_index_start), In_index_start, record_index - 1);
		Node->rchild = create_BinTree(pre,In,(record_index - In_index_start)+1+pre_index_start,pre_index_end,record_index+1,In_index_end);
		return Node;
	}
}

void PreOrder(BinTree T)
{
	if (T != NULL)    //如果该节点不为NULL
	{
		cout << T->data << " ";
		PreOrder(T->lchild);
		PreOrder(T->rchild);
	}
}


int main()
{
	char a[] = "ABDGCEF"; //先序遍历
	char b[] = "DGBAECF";//中序遍历
	BinTree root = (BinTree)malloc(sizeof(BinTNode));
	root=create_BinTree(a, b,0,strlen(a)-1,0,strlen(b)-1);
	printf("先序遍历的结果是：");
	PreOrder(root);

}

最后

以上就是快乐金针菇为你收集整理的已知先序与中序遍历结果构建二叉树(C++版)的全部内容，希望文章能够帮你解决已知先序与中序遍历结果构建二叉树(C++版)所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。