1. 首页
  2. 文章中心
  3. JAVASE

TreeSet集合的概述和特点和与TreeMap源码分析概述特点代码实现与TreeMap对比源码分析

68 阅读 0 评论
我是靠谱客的博主 感动帅哥，最近开发中收集的这篇文章主要介绍TreeSet集合的概述和特点和与TreeMap源码分析概述特点代码实现与TreeMap对比源码分析，觉得挺不错的，现在分享给大家，希望可以做个参考。

概述

TreeSet集合的概述和特点和源码分析

  • 概述
  • 特点
  • 代码实现
  • 与TreeMap对比源码分析
    • TreeSet
    • TreeMap

概述

图:
柏维怡我爱你

特点

TreeSet集合的特点:

  1. 元素有序:注意不是说存储和取出的元素有序,而是按照一定的规则进行有序,具体的有序方式取决于构造器
  • TreeSet();根据元素自然进行排序
  • TreeSet(Comparator comparator); 根据指定的比较器进行排序
  1. 没有带索引方法,所以不能使用普通for循环遍历
  2. 由于是间接实现Set集合,所以不包含重复的元素的集合

代码实现

package CCom.Cnn;

import java.util.TreeSet;

public class Demo {
    public static void main(String[] args) {
        //创建集合对象
        TreeSet<Integer> i = new TreeSet<>();
        //添加元素
        i.add(10);
        i.add(20);
        i.add(30);
        i.add(40);
        i.add(50);

        i.add(30);

        //遍历集合
        for (Integer x:i) {
            System.out.println(x.intValue());//注意是int型的数值哦
        }
    }
}

输出的内容
10
20
30
40
50

与TreeMap对比源码分析

TreeSet

  • 主要为大家详细介绍了java中treemap和treeset实现红黑树，具有一定的参考价值
  • TreeMap 的实现就是红黑树数据结构，也就说是一棵自平衡的排序二叉树，这样就可以保证当需要快速检索指定节点

源码分析1：

public class TreeSet<E> extends AbstractSet<E>
implements NavigableSet<E>, Cloneable, java.io.Serializable
{
// 使用 NavigableMap 的 key 来保存 Set 集合的元素
private transient NavigableMap<E,Object> m;
// 使用一个 PRESENT 作为 Map 集合的所有 value。
private static final Object PRESENT = new Object();
// 包访问权限的构造器，以指定的 NavigableMap 对象创建 Set 集合
TreeSet(NavigableMap<E,Object> m)
{
this.m = m;
}
public TreeSet() // ①
{
// 以自然排序方式创建一个新的 TreeMap，
// 根据该 TreeSet 创建一个 TreeSet，
// 使用该 TreeMap 的 key 来保存 Set 集合的元素
this(new TreeMap<E,Object>());
}
public TreeSet(Comparator<? super E> comparator) // ②
{
// 以定制排序方式创建一个新的 TreeMap，
// 根据该 TreeSet 创建一个 TreeSet，
// 使用该 TreeMap 的 key 来保存 Set 集合的元素
this(new TreeMap<E,Object>(comparator));
}
public TreeSet(Collection<? extends E> c)
{
// 调用①号构造器创建一个 TreeSet，底层以 TreeMap 保存集合元素
this();
// 向 TreeSet 中添加 Collection 集合 c 里的所有元素
addAll(c);
}
public TreeSet(SortedSet<E> s)
{
// 调用②号构造器创建一个 TreeSet，底层以 TreeMap 保存集合元素
this(s.comparator());
// 向 TreeSet 中添加 SortedSet 集合 s 里的所有元素
addAll(s);
}
//TreeSet 的其他方法都只是直接调用 TreeMap 的方法来提供实现
...
public boolean addAll(Collection<? extends E> c)
{
if (m.size() == 0 && c.size() > 0 &&
c instanceof SortedSet &&
m instanceof TreeMap)
{
// 把 c 集合强制转换为 SortedSet 集合
SortedSet<? extends E> set = (SortedSet<? extends E>) c;
// 把 m 集合强制转换为 TreeMap 集合
TreeMap<E,Object> map = (TreeMap<E, Object>) m;
Comparator<? super E> cc = (Comparator<? super E>) set.comparator();
Comparator<? super E> mc = map.comparator();
// 如果 cc 和 mc 两个 Comparator 相等
if (cc == mc || (cc != null && cc.equals(mc)))
{
// 把 Collection 中所有元素添加成 TreeMap 集合的 key
map.addAllForTreeSet(set, PRESENT);
return true;
}
}
// 直接调用父类的 addAll() 方法来实现
return super.addAll(c);
}
...
}

从上面代码可以看出，TreeSet 的 ① 号、② 号构造器的都是新建一个 TreeMap 作为实际存储 Set 元素的容器，而另外 2 个构造器则分别依赖于 ① 号和 ② 号构造器，由此可见，TreeSet 底层实际使用的存储容器就是 TreeMap

  • 与 HashSet 完全类似的是，TreeSet 里绝大部分方法都是直接调用 TreeMap 的方法来实现的，这一点读者可以自行参阅TreeSet 的源代码，此处就不再给出了
  • 对于 TreeMap 而言，它采用一种被称为“红黑树”的排序二叉树来保存 Map 中每个 Entry —— 每个 Entry 都被当成“红黑树”的一个节点对待。例如对于如下程序而言：
public class TreeMapTest
{
public static void main(String[] args)
{
TreeMap<String , Double> map =
new TreeMap<String , Double>();
map.put("ccc" , 89.0);
map.put("aaa" , 80.0);
map.put("zzz" , 80.0);
map.put("bbb" , 89.0);
System.out.println(map);
}
}

当程序执行 map.put(“ccc” , 89.0); 时，系统将直接把 “ccc”-89.0 这个 Entry 放入 Map 中，这个 Entry 就是该“红黑树”的根节点。接着程序执行 map.put(“aaa” , 80.0); 时，程序会将 “aaa”-80.0 作为新节点添加到已有的红黑树中。

  • 以后每向 TreeMap 中放入一个 key-value 对，系统都需要将该 Entry 当成一个新节点，添加成已有红黑树中，通过这种方式就可保证 TreeMap 中所有 key 总是由小到大地排列。例如我们输出上面程序，将看到如下结果（所有 key 由小到大地排列）：
    {aaa=80.0, bbb=89.0, ccc=89.0, zzz=80.0}

TreeMap

  1. 红黑树
    红黑树是一种自平衡排序二叉树，树中每个节点的值，都大于或等于在它的左子树中的所有节点的值，并且小于或等于在它的右子树中的所有节点的值，这确保红黑树运行时可以快速地在树中查找和定位的所需节点。

  2. 对于 TreeMap 而言，由于它底层采用一棵“红黑树”来保存集合中的 Entry，这意味这 TreeMap 添加元素、取出元素的性能都比 HashMap 低：当 TreeMap 添加元素时，需要通过循环找到新增 Entry 的插入位置，因此比较耗性能；当从 TreeMap 中取出元素时，需要通过循环才能找到合适的 Entry，也比较耗性能。但 TreeMap、TreeSet 比 HashMap、HashSet 的优势在于：TreeMap 中的所有 Entry 总是按 key 根据指定排序规则保持有序状态，TreeSet 中所有元素总是根据指定排序规则保持有序状态

  3. 为了理解 TreeMap 的底层实现，必须先介绍排序二叉树和红黑树这两种数据结构。其中红黑树又是一种特殊的排序二叉树

  4. 排序二叉树是一种特殊结构的二叉树，可以非常方便地对树中所有节点进行排序和检索

  5. 排序二叉树要么是一棵空二叉树，要么是具有下列性质的二叉树：

    • 若它的左子树不空，则左子树上所有节点的值均小于它的根节点的值；
    • 若它的右子树不空，则右子树上所有节点的值均大于它的根节点的值；
    • 它的左、右子树也分别为排序二叉树。

  6. 图 1 显示了一棵排序二叉树：
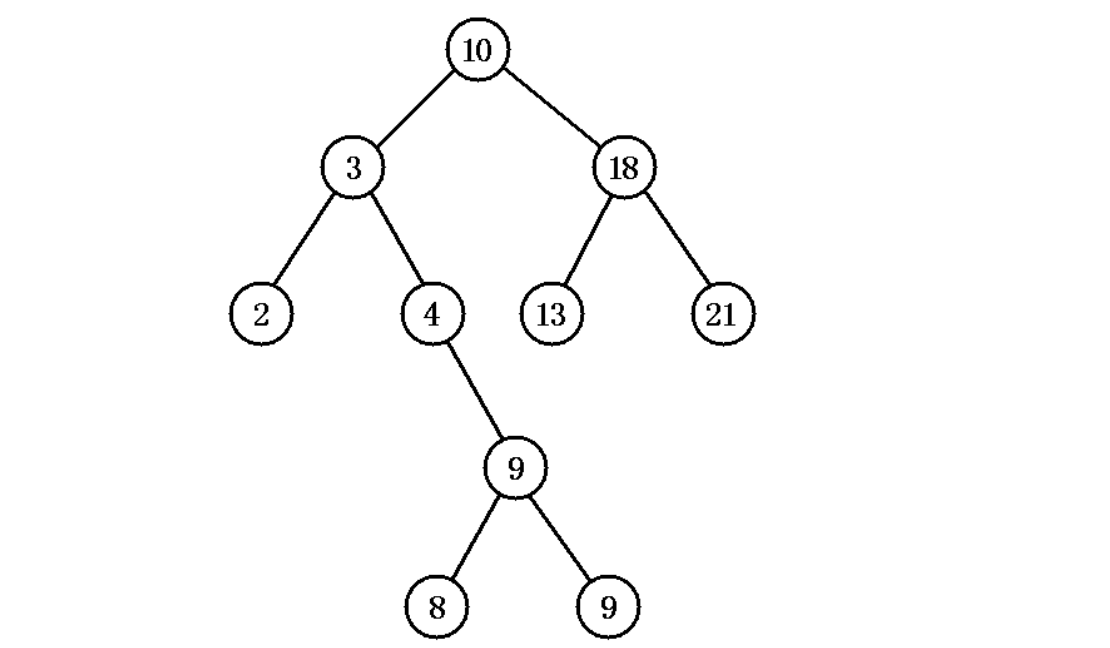
    在这里插入图片描述
    对排序二叉树，若按中序遍历就可以得到由小到大的有序序列。如图 1 所示二叉树，中序遍历得：
    {2，3，4，8，9，9，10，13，15，18}

创建排序二叉树的步骤，也就是不断地向排序二叉树添加节点的过程，向排序二叉树添加节点的步骤如下：

  1. 以根节点当前节点开始搜索。
  2. 拿新节点的值和当前节点的值比较。
  3. 如果新节点的值更大，则以当前节点的右子节点作为新的当前节点；如果新节点的值更小，则以当前的左子节点作为新的当前节点。
  4. 重复 2、3 两个步骤，直到搜索到合适的叶子节点为止。
  5. 将新节点添加为第 4 步找到的叶子节点的子节点；如果新节点更大，则添加为右子节点；否则添加为左子节点。

掌握上面理论之后，下面我们来分析 TreeMap 添加节点（TreeMap 中使用 Entry 内部类代表节点）的实现，TreeMap 集合的put(K key, V value) 方法实现了将 Entry 放入排序二叉树中，下面是该方法的源代码：

源码分析

public V put(K key, V value)
{
// 先以 t 保存链表的 root 节点
Entry<K,V> t = root;
// 如果 t==null，表明是一个空链表，即该 TreeMap 里没有任何 Entry
if (t == null)
{
// 将新的 key-value 创建一个 Entry，并将该 Entry 作为 root
root = new Entry<K,V>(key, value, null);
// 设置该 Map 集合的 size 为 1，代表包含一个 Entry
size = 1;
// 记录修改次数为 1
modCount++;
return null;
}
int cmp;
Entry<K,V> parent;
Comparator<? super K> cpr = comparator;
// 如果比较器 cpr 不为 null，即表明采用定制排序
if (cpr != null)
{
do {
// 使用 parent 上次循环后的 t 所引用的 Entry
parent = t;
// 拿新插入 key 和 t 的 key 进行比较
cmp = cpr.compare(key, t.key);
// 如果新插入的 key 小于 t 的 key，t 等于 t 的左边节点
if (cmp < 0)
t = t.left;
// 如果新插入的 key 大于 t 的 key，t 等于 t 的右边节点
else if (cmp > 0)
t = t.right;
// 如果两个 key 相等，新的 value 覆盖原有的 value，
// 并返回原有的 value
else
return t.setValue(value);
} while (t != null);
}
else
{
if (key == null)
throw new NullPointerException();
Comparable<? super K> k = (Comparable<? super K>) key;
do {
// 使用 parent 上次循环后的 t 所引用的 Entry
parent = t;
// 拿新插入 key 和 t 的 key 进行比较
cmp = k.compareTo(t.key);
// 如果新插入的 key 小于 t 的 key，t 等于 t 的左边节点
if (cmp < 0)
t = t.left;
// 如果新插入的 key 大于 t 的 key，t 等于 t 的右边节点
else if (cmp > 0)
t = t.right;
// 如果两个 key 相等，新的 value 覆盖原有的 value，
// 并返回原有的 value
else
return t.setValue(value);
} while (t != null);
}
// 将新插入的节点作为 parent 节点的子节点
Entry<K,V> e = new Entry<K,V>(key, value, parent);
// 如果新插入 key 小于 parent 的 key，则 e 作为 parent 的左子节点
if (cmp < 0)
parent.left = e;
// 如果新插入 key 小于 parent 的 key，则 e 作为 parent 的右子节点
else
parent.right = e;
// 修复红黑树
fixAfterInsertion(e); // ①
size++;
modCount++;
return null;
}

上面程序中粗体字代码就是实现“排序二叉树”的关键算法，每当程序希望添加新节点时：系统总是从树的根节点开始比较 ——即将根节点当成当前节点，如果新增节点大于当前节点、并且当前节点的右子节点存在，则以右子节点作为当前节点；如果新增节点小于当前节点、并且当前节点的左子节点存在，则以左子节点作为当前节点；如果新增节点等于当前节点，则用新增节点覆盖当前节点，并结束循环 —— 直到找到某个节点的左、右子节点不存在，将新节点添加该节点的子节点 —— 如果新节点比该节点大，则添加为右子节点；如果新节点比该节点小，则添加为左子节点

  • 1. TreeMap 的删除节点
    当程序从排序二叉树中删除一个节点之后，为了让它依然保持为排序二叉树，程序必须对该排序二叉树进行维护。维护可分为如下几种情况：
    （1）被删除的节点是叶子节点，则只需将它从其父节点中删除即可。
    （2）被删除节点 p 只有左子树，将 p 的左子树 pL 添加成 p 的父节点的左子树即可；被删除节点 p 只有右子树，将 p 的右子
    树 pR 添加成 p 的父节点的右子树即可。
    （3）若被删除节点 p 的左、右子树均非空，有两种做法：
    • 将 pL 设为 p 的父节点 q 的左或右子节点（取决于 p 是其父节点 q 的左、右子节点），将 pR 设为 p 节点的中序前趋节点 s 的右子节点（s 是 pL 最右下的节点，也就是 pL 子树中最大的节点）。以 p 节点的中序前趋或后继替代 p 所指节点，然后再从原排序二叉树中删去中序前趋或后继节点即可。（也就是用大于 p 的最小节点或小于 p 的最大节点代替 p 节点即可）
    • 显示了被删除节点只有左子树的示意图
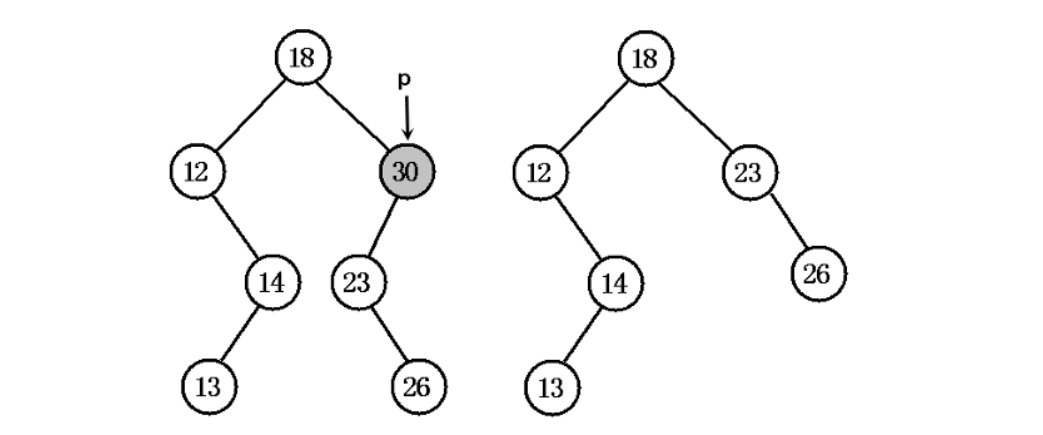
    • 在这里插入图片描述
    • 显示了被删除节点只有右子树的示意图：
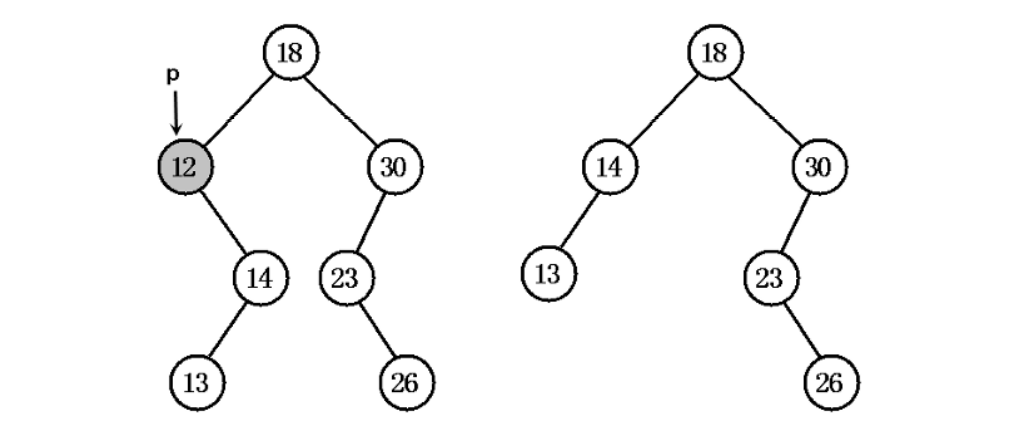
    • 在这里插入图片描述
    • 显示了被删除节点既有左子节点，又有右子节点的情形，此时我们采用到是第一种方式进行维护：
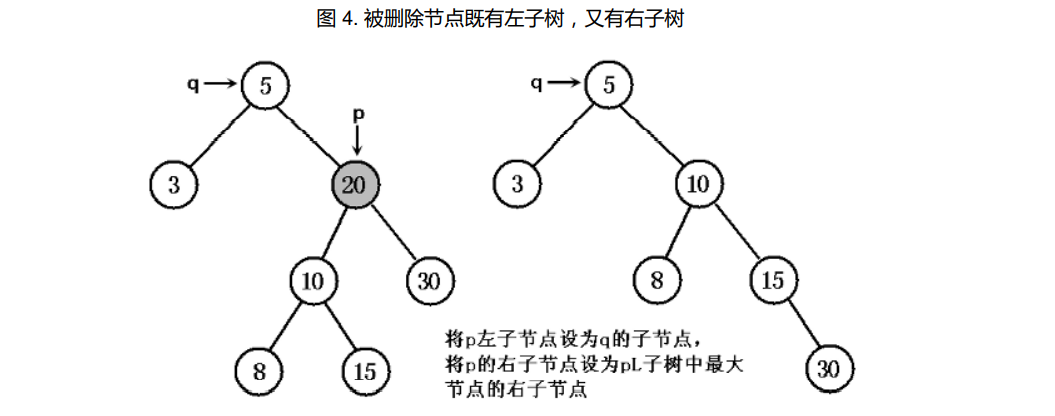
    • 在这里插入图片描述
    • 被删除节点既有左子树，又有右子树
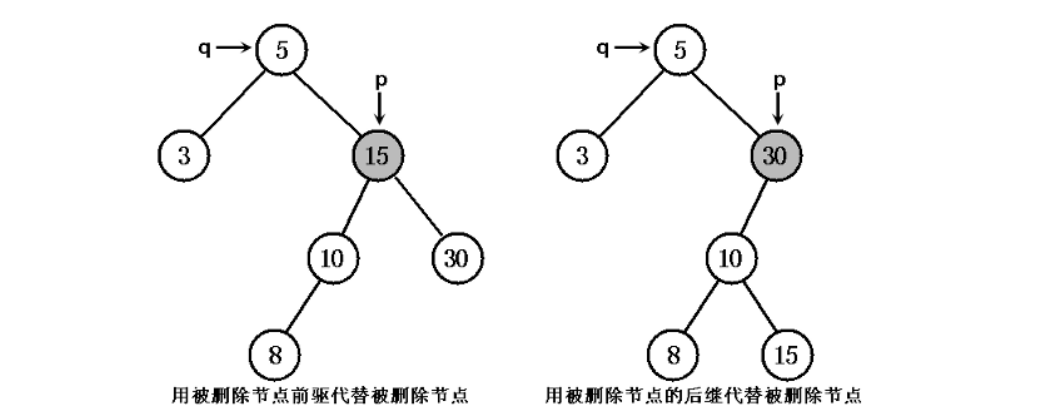
    • 在这里插入图片描述
      TreeMap 删除节点采用图 5 所示右边的情形进行维护——也就是用被删除节点的右子树中最小节点与被删节点交换的方式进行维护。

. TreeMap 删除节点的方法由如下方法实现:

private void deleteEntry(Entry<K,V> p)
{
modCount++;
size--;
// 如果被删除节点的左子树、右子树都不为空
if (p.left != null && p.right != null)
{
// 用 p 节点的中序后继节点代替 p 节点
Entry<K,V> s = successor (p);
p.key = s.key;
p.value = s.value;
p = s;
}
// 如果 p 节点的左节点存在，replacement 代表左节点；否则代表右节点。
Entry<K,V> replacement = (p.left != null ? p.left : p.right);
if (replacement != null)
{
replacement.parent = p.parent;
// 如果 p 没有父节点，则 replacemment 变成父节点
if (p.parent == null)
root = replacement;
// 如果 p 节点是其父节点的左子节点
else if (p == p.parent.left)
p.parent.left = replacement;
// 如果 p 节点是其父节点的右子节点
else
p.parent.right = replacement;
p.left = p.right = p.parent = null;
// 修复红黑树
if (p.color == BLACK)
fixAfterDeletion(replacement); // ①
}
// 如果 p 节点没有父节点
else if (p.parent == null)
{
root = null;
}
else
{
if (p.color == BLACK)
// 修复红黑树
fixAfterDeletion(p); // ②
if (p.parent != null)
{
// 如果 p 是其父节点的左子节点
if (p == p.parent.left)
p.parent.left = null;
// 如果 p 是其父节点的右子节点
else if (p == p.parent.right)
p.parent.right = null;
p.parent = null;
}
}
}

TreeMap 为插入节点后的修复操作由 fixAfterInsertion(Entry<K,V> x) 方法提供，该方法的源代码如下：

// 插入节点后修复红黑树
private void fixAfterInsertion(Entry<K,V> x)
{
x.color = RED;
// 直到 x 节点的父节点不是根，且 x 的父节点不是红色
while (x != null && x != root
&& x.parent.color == RED)
{
// 如果 x 的父节点是其父节点的左子节点
if (parentOf(x) == leftOf(parentOf(parentOf(x))))
{
// 获取 x 的父节点的兄弟节点
Entry<K,V> y = rightOf(parentOf(parentOf(x)));
// 如果 x 的父节点的兄弟节点是红色
if (colorOf(y) == RED)
{
// 将 x 的父节点设为黑色
setColor(parentOf(x), BLACK);
// 将 x 的父节点的兄弟节点设为黑色
setColor(y, BLACK);
// 将 x 的父节点的父节点设为红色
setColor(parentOf(parentOf(x)), RED);
x = parentOf(parentOf(x));
}
// 如果 x 的父节点的兄弟节点是黑色
else
{
// 如果 x 是其父节点的右子节点
if (x == rightOf(parentOf(x)))
{
// 将 x 的父节点设为 x
x = parentOf(x);
rotateLeft(x);
}
// 把 x 的父节点设为黑色
setColor(parentOf(x), BLACK);
// 把 x 的父节点的父节点设为红色
setColor(parentOf(parentOf(x)), RED);
rotateRight(parentOf(parentOf(x)));
}
}
// 如果 x 的父节点是其父节点的右子节点
else
{
// 获取 x 的父节点的兄弟节点
Entry<K,V> y = leftOf(parentOf(parentOf(x)));
// 如果 x 的父节点的兄弟节点是红色
if (colorOf(y) == RED)
{
// 将 x 的父节点设为黑色。
setColor(parentOf(x), BLACK);
// 将 x 的父节点的兄弟节点设为黑色
setColor(y, BLACK);
// 将 x 的父节点的父节点设为红色
setColor(parentOf(parentOf(x)), RED);
// 将 x 设为 x 的父节点的节点
x = parentOf(parentOf(x));
}
// 如果 x 的父节点的兄弟节点是黑色
else
{
// 如果 x 是其父节点的左子节点
if (x == leftOf(parentOf(x)))
{
// 将 x 的父节点设为 x
x = parentOf(x);
rotateRight(x);
}
// 把 x 的父节点设为黑色
setColor(parentOf(x), BLACK);
// 把 x 的父节点的父节点设为红色
setColor(parentOf(parentOf(x)), RED);
rotateLeft(parentOf(parentOf(x)));
}
}
}
// 将根节点设为黑色
root.color = BLACK;
}

删除节点后的修复:

与添加节点之后的修复类似的是，TreeMap 删除节点之后也需要进行类似的修复操作，通过这种修复来保证该排序二叉树依然满足红黑树特征。大家可以参考插入节点之后的修复来分析删除之后的修复。TreeMap 在删除之后的修复操作由fixAfterDeletion(Entry<K,V> x) 方法提供，该方法源代码如下：

// 删除节点后修复红黑树
private void fixAfterDeletion(Entry<K,V> x)
{
// 直到 x 不是根节点，且 x 的颜色是黑色
while (x != root && colorOf(x) == BLACK)
{
// 如果 x 是其父节点的左子节点
if (x == leftOf(parentOf(x)))
{
// 获取 x 节点的兄弟节点
Entry<K,V> sib = rightOf(parentOf(x));
// 如果 sib 节点是红色
if (colorOf(sib) == RED)
{
// 将 sib 节点设为黑色
setColor(sib, BLACK);
// 将 x 的父节点设为红色
setColor(parentOf(x), RED);
rotateLeft(parentOf(x));
// 再次将 sib 设为 x 的父节点的右子节点
sib = rightOf(parentOf(x));
}
// 如果 sib 的两个子节点都是黑色
if (colorOf(leftOf(sib)) == BLACK
&& colorOf(rightOf(sib)) == BLACK)
{
// 将 sib 设为红色
setColor(sib, RED);
// 让 x 等于 x 的父节点
x = parentOf(x);
}
else
{
// 如果 sib 的只有右子节点是黑色
if (colorOf(rightOf(sib)) == BLACK)
{
// 将 sib 的左子节点也设为黑色
setColor(leftOf(sib), BLACK);
// 将 sib 设为红色
setColor(sib, RED);
rotateRight(sib);
sib = rightOf(parentOf(x));
}
// 设置 sib 的颜色与 x 的父节点的颜色相同
setColor(sib, colorOf(parentOf(x)));
// 将 x 的父节点设为黑色
setColor(parentOf(x), BLACK);
// 将 sib 的右子节点设为黑色
setColor(rightOf(sib), BLACK);
rotateLeft(parentOf(x));
x = root;
}
}
// 如果 x 是其父节点的右子节点
else
{
// 获取 x 节点的兄弟节点
Entry<K,V> sib = leftOf(parentOf(x));
// 如果 sib 的颜色是红色
if (colorOf(sib) == RED)
{
// 将 sib 的颜色设为黑色
setColor(sib, BLACK);
// 将 sib 的父节点设为红色
setColor(parentOf(x), RED);
rotateRight(parentOf(x));
sib = leftOf(parentOf(x));
}
// 如果 sib 的两个子节点都是黑色
if (colorOf(rightOf(sib)) == BLACK
&& colorOf(leftOf(sib)) == BLACK)
{
// 将 sib 设为红色
setColor(sib, RED);
// 让 x 等于 x 的父节点
x = parentOf(x);
}
else
{
// 如果 sib 只有左子节点是黑色
if (colorOf(leftOf(sib)) == BLACK)
{
// 将 sib 的右子节点也设为黑色
setColor(rightOf(sib), BLACK);
// 将 sib 设为红色
setColor(sib, RED);
rotateLeft(sib);
sib = leftOf(parentOf(x));
}
// 将 sib 的颜色设为与 x 的父节点颜色相同
setColor(sib, colorOf(parentOf(x)));
// 将 x 的父节点设为黑色
setColor(parentOf(x), BLACK);
// 将 sib 的左子节点设为黑色
setColor(leftOf(sib), BLACK);
rotateRight(parentOf(x));
x = root;
}
}
}
setColor(x, BLACK);
}

检索节点:
当 TreeMap 根据 key 来取出 value 时，TreeMap 对应的方法如下：

public V get(Object key)
{
// 根据指定 key 取出对应的 Entry
Entry>K,V< p = getEntry(key);
// 返回该 Entry 所包含的 value
return (

从上面程序的粗体字代码可以看出，get(Object key) 方法实质是由于 getEntry() 方法实现的，这个 getEntry() 方法的代码如下：

final Entry<K,V> getEntry(Object key)
{
// 如果 comparator 不为 null，表明程序采用定制排序
if (comparator != null)
// 调用 getEntryUsingComparator 方法来取出对应的 key
return getEntryUsingComparator(key);
// 如果 key 形参的值为 null，抛出 NullPointerException 异常
if (key == null)
throw new NullPointerException();
// 将 key 强制类型转换为 Comparable 实例
Comparable<? super K> k = (Comparable<? super K>) key;
// 从树的根节点开始
Entry<K,V> p = root;
while (p != null)
{
// 拿 key 与当前节点的 key 进行比较
int cmp = k.compareTo(p.key);
// 如果 key 小于当前节点的 key，向“左子树”搜索
if (cmp < 0)
p = p.left;
// 如果 key 大于当前节点的 key，向“右子树”搜索
else if (cmp > 0)
p = p.right;
// 不大于、不小于，就是找到了目标 Entry
else
return p;
}
return null;
}

上面的 getEntry(Object obj) 方法也是充分利用排序二叉树的特征来搜索目标 Entry，程序依然从二叉树的根节点开始，如果被搜索节点大于当前节点，程序向“右子树”搜索；如果被搜索节点小于当前节点，程序向“左子树”搜索；如果相等，那就是找到了指定节点。

  • 当 TreeMap 里的 comparator != null 即表明该 TreeMap 采用了定制排序，在采用定制排序的方式下，TreeMap 采用getEntryUsingComparator(key) 方法来根据 key 获取 Entry。下面是该方法的代码：
final Entry<K,V> getEntryUsingComparator(Object key)
{
K k = (K) key;
// 获取该 TreeMap 的 comparator
Comparator<? super K> cpr = comparator;
if (cpr != null)
{
// 从根节点开始
Entry<K,V> p = root;
while (p != null)
{
// 拿 key 与当前节点的 key 进行比较
int cmp = cpr.compare(k, p.key);
// 如果 key 小于当前节点的 key，向“左子树”搜索
if (cmp < 0)
p = p.left;
// 如果 key 大于当前节点的 key，向“右子树”搜索
else if (cmp > 0)
p = p.right;
// 不大于、不小于，就是找到了目标 Entry
else
return p;
}
}
return null;
}

其实 getEntry、getEntryUsingComparator 两个方法的实现思路完全类似，只是前者对自然排序的 TreeMap 获取有效，后者对定制排序的 TreeMap 有效，

通过上面源代码的分析不难看出，TreeMap 这个工具类的实现其实很简单。或者说：从内部结构来看，TreeMap 本质上就是一棵“红黑树”，而 TreeMap 的每个 Entry 就是该红黑树的一个节点。

最后

以上就是感动帅哥为你收集整理的TreeSet集合的概述和特点和与TreeMap源码分析概述特点代码实现与TreeMap对比源码分析的全部内容，希望文章能够帮你解决TreeSet集合的概述和特点和与TreeMap源码分析概述特点代码实现与TreeMap对比源码分析所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。

本图文内容来源于网友提供，作为学习参考使用，或来自网络收集整理，版权属于原作者所有。
点赞(45)

相关文章

集合框架-TreeSet集合
集合框架-TreeSet集合
TreeSet的特点...
TreeSet的特点...
Java TreeSet集合概述和特点
Java TreeSet集合概述和特点
String类的常用方法String类的常用方法
String类的常用方法String类的常用方法
TreeSet集合的概述和特点和与TreeMap源码分析概述特点代码实现与TreeMap对比源码分析
TreeSet集合的概述和特点和与TreeMap源码分析概述特点代码实现与TreeMap对比源码分析
TreeSet集合
TreeSet集合
黑马程序员：Java基础总结----枚举
黑马程序员：Java基础总结----枚举
黑马程序员：java基础知识（二）
黑马程序员：java基础知识（二）

评论列表共有 0 条评论

立即
投稿
返回
顶部