本系列博客基于温州大学黄海广博士的机器学习课程的笔记,小伙伴们想更详细学习黄博士课程请移步到黄博士的Github、或者机器学习初学者公众号,现在在中国慕课也是可以学习的,内容包括机器学习、深度学习及Python编程,matplotlib、numpy、pandas、sklearn等,资料很详细,要系统学习请移步哦!笔者的博客只是笔记,内容不会十分详细,甚至会有些少错误!
1.降维概述
-
维数灾难:在机器学习建模过程中,随着特征数量的增多,计算量会剧增,变得很大,维度太大导致机器学习性能下降,模型的性能随着特征的增加先上升后下降;
-
降维定义:降维(Dimensionality Reduction),将训练数据中的样本从高维空间转换到低维空间,但不存在完全无损的降维;
-
降维的意义:
- 高维数据增加了运算难度;
- 高维使得学习算法的泛化额能力变弱,维度越高,算法的搜索难度和成本越大;
- 降维增加数据可读性,有利于发掘数据有意义的结构;
-
降维的作用:
- 减少冗余特征,降低数据维度;
假设有两个特征:
x 1 x_1 x1:身高(单位:厘米);
x 2 x_2 x2:身高(单位:英寸);
可以用一个特征表示身高即可; - 数据可视化;
t − d i s t r i b u t e d S t o c h a s t i c N e i g h b o r E m b e d d i n g ( t − S N E ) t-distributed Stochastic Neighbor Embedding(t-SNE) t−distributedStochasticNeighborEmbedding(t−SNE):将数据点之间的相似度转换为概率;
- 减少冗余特征,降低数据维度;
-
降维的优缺点:
-
优点:
- 通过减少特征的维数,数据集存储所需的空间相应减少,减少了特征维数所需的计算训练时间;
- 数据集特征的降维有助于快速可视化数据;
- 通过处理多重共线性消除冗余特征;
-
缺点:
- 降维可能会丢失一些数据;
- 在主成分分析(PCA)降维技术中,有时需要考虑多少主成分是难以确定的;
2.SVD(奇异值分解)
2.1 奇异值分解
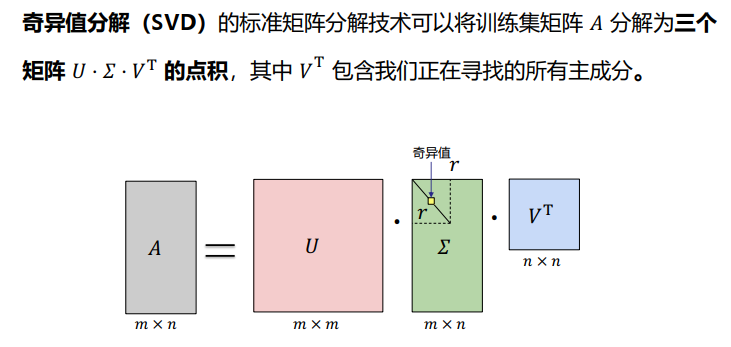
- 奇异值分解 ( S i n g u l a r V a l u e D e c o m p o s i t i o n , S V D ) (Singular Value Decomposition,SVD) (Singular Value Decomposition,SVD);
- SVD可以将一个矩阵
A
A
A分解成三个矩阵的乘积:
- 一个正交矩阵 U ( o r t h o g o n a l m a t r i x ) U(orthogonal matrix) U(orthogonal matrix);
- 一个对角矩阵 Σ ( d i a g o n a l m a t r i x ) Sigma(diagonal matrix) Σ(diagonal matrix);
- 一个正交矩阵 V V V的转置;
2.2 SVD详解
-
假设矩阵 A A A是一个 m × n mtimes{n} m×n的矩阵,通过 S V D SVD SVD对矩阵进行分解, S V D SVD SVD定义如下:
A = U Σ V T A=USigma{V^T} A=UΣVT
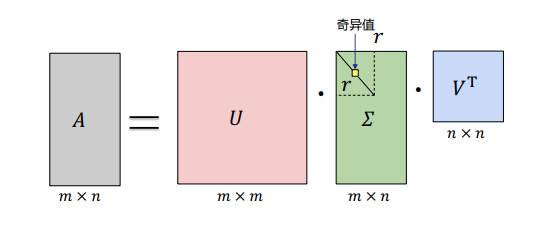
-
符号定义
A = U Σ V T = u 1 σ 1 v 1 T + ⋯ + u r σ r v r T A=USigma{V^T}=u_1sigma_1v_1^T+dots+u_rsigma_rv_r^T A=UΣVT=u1σ1v1T+⋯+urσrvrT
其 中 : U : 一 个 m × m 的 矩 阵 ; 每 个 特 征 向 量 u i 称 为 A 的 左 奇 异 向 量 ; Σ : 一 个 m × n 的 矩 阵 ; 除 了 主 对 角 线 上 的 元 素 以 外 全 为 0 , 主 对 角 线 上 的 每 个 元 素 都 称 为 奇 异 值 σ ; V : 一 个 n × n 的 矩 阵 , 每 个 特 征 向 量 v i 称 为 A 的 右 奇 异 向 量 ; U 和 V 都 是 酉 矩 阵 , 即 满 足 : U T U = I , V T V = I ; r : 矩 阵 A 的 秩 ; 其中:\ U:一个mtimes{m}的矩阵;每个特征向量u_i称为A的左奇异向量;\ Sigma:一个mtimes{n}的矩阵;除了主对角线上的元素以外全为0,主对角线上的每个元素都称为奇异值sigma;\ V:一个ntimes{n}的矩阵,每个特征向量v_i称为A的右奇异向量;\ U和V都是酉矩阵,即满足:U^TU=I,V^TV=I;\ r:矩阵A的秩; 其中:U:一个m×m的矩阵;每个特征向量ui称为A的左奇异向量;Σ:一个m×n的矩阵;除了主对角线上的元素以外全为0,主对角线上的每个元素都称为奇异值σ;V:一个n×n的矩阵,每个特征向量vi称为A的右奇异向量;U和V都是酉矩阵,即满足:UTU=I,VTV=I;r:矩阵A的秩; -
SVD求解1:U矩阵求解
方 阵 A A T 为 m × m 的 一 个 方 阵 , 可 以 进 行 特 征 分 解 , 得 到 的 特 征 值 和 特 征 向 量 满 足 式 子 : ( A A T ) u i = λ i u i 得 到 矩 阵 A A T 的 m 个 特 征 值 和 对 应 的 m 个 特 征 向 量 u ; 将 A A T 的 所 有 特 征 向 量 组 成 一 个 m × m 的 矩 阵 U , 即 S V D 中 的 U 矩 阵 ; U 矩 阵 中 的 每 个 特 征 向 量 叫 做 A 的 左 奇 异 向 量 ; 方阵AA^T为mtimes{m}的一个方阵,可以进行特征分解,得到的特征值和特征向量满足式子:(AA^T)u_i=lambda_iu_i\ 得到矩阵AA^T的m个特征值和对应的m个特征向量u;\ 将AA^T的所有特征向量组成一个mtimes{m}的矩阵U,即SVD中的U矩阵;\ U矩阵中的每个特征向量叫做A的左奇异向量; 方阵AAT为m×m的一个方阵,可以进行特征分解,得到的特征值和特征向量满足式子:(AAT)ui=λiui得到矩阵AAT的m个特征值和对应的m个特征向量u;将AAT的所有特征向量组成一个m×m的矩阵U,即SVD中的U矩阵;U矩阵中的每个特征向量叫做A的左奇异向量; -
SVD求解2:V矩阵求解
将 A 的 转 置 和 A 做 矩 阵 乘 法 , 得 到 一 个 n × n 的 一 个 方 阵 A T A ; 特 征 分 解 , 得 到 特 征 值 和 特 征 向 量 满 足 : ( A T A ) v i = λ i v i ; 得 到 矩 阵 A T A 的 n 个 特 征 值 和 对 应 的 n 个 特 征 向 量 v ; 将 A T A 的 所 有 特 征 向 量 组 成 一 个 n × n 的 矩 阵 V , 即 S V D 中 V 矩 阵 ; V 矩 阵 中 的 每 个 特 征 向 量 叫 做 A 的 右 奇 异 向 量 ; 将A的转置和A做矩阵乘法,得到一个ntimes{n}的一个方阵A^TA;\ 特征分解,得到特征值和特征向量满足:(A^TA)v_i=lambda_iv_i;\ 得到矩阵A^TA的n个特征值和对应的n个特征向量v;\ 将A^TA的所有特征向量组成一个ntimes{n}的矩阵V,即SVD中V矩阵;\ V矩阵中的每个特征向量叫做A的右奇异向量; 将A的转置和A做矩阵乘法,得到一个n×n的一个方阵ATA;特征分解,得到特征值和特征向量满足:(ATA)vi=λivi;得到矩阵ATA的n个特征值和对应的n个特征向量v;将ATA的所有特征向量组成一个n×n的矩阵V,即SVD中V矩阵;V矩阵中的每个特征向量叫做A的右奇异向量; -
SVD求解3: Σ Sigma Σ矩阵求解
特 征 值 矩 阵 等 于 奇 异 值 矩 阵 的 平 方 , 即 特 征 值 和 奇 异 值 满 足 : σ i = λ i ; 可 以 通 过 A T A 的 特 征 值 取 平 方 根 求 解 奇 异 值 ; 由 A = U Σ V T , 则 有 : A V = U Σ V T V ; 因 : V T V = I , 则 有 : A V = U Σ ; 有 : A v i = σ i u i , σ i = A v i / u i 特征值矩阵等于奇异值矩阵的平方,即特征值和奇异值满足:sigma_i=sqrt{lambda_i};\ 可以通过A^TA的特征值取平方根求解奇异值;\ 由A=USigma{V^T},则有:AV=USigma{V^T}V;\ 因:V^TV=I,则有:AV=USigma;\ 有:Av_i=sigma_iu_i,sigma_i=Av_i/u_i 特征值矩阵等于奇异值矩阵的平方,即特征值和奇异值满足:σi=λi;可以通过ATA的特征值取平方根求解奇异值;由A=UΣVT,则有:AV=UΣVTV;因:VTV=I,则有:AV=UΣ;有:Avi=σiui,σi=Avi/ui
2.3 SVD计算案例
-
实例背景
设 矩 阵 A 定 义 : A = [ 3 0 4 5 ] , 则 有 A 的 秩 r = 2 设矩阵A定义:A=begin{bmatrix}3 & 0\4 & 5end{bmatrix},则有A的秩r=2 设矩阵A定义:A=[3405],则有A的秩r=2; -
求 A T A 和 A A T A^TA和AA^T ATA和AAT
A T A = [ 3 4 0 5 ] [ 3 0 4 5 ] = [ 25 20 20 25 ] ; A A T = [ 3 0 4 5 ] [ 3 4 0 5 ] = [ 9 12 12 41 ] A^TA=begin{bmatrix}3 & 4\0 & 5end{bmatrix}begin{bmatrix}3 & 0\4 & 5end{bmatrix}=begin{bmatrix}25 & 20\20 & 25end{bmatrix}; AA^T=begin{bmatrix}3 & 0\4 & 5end{bmatrix}begin{bmatrix}3 & 4\0 & 5end{bmatrix}=begin{bmatrix}9 & 12\12 & 41end{bmatrix} ATA=[3045][3405]=[25202025]; AAT=[3405][3045]=[9121241] -
计算 A T A A^TA ATA的特征值和特征向量
∣ 25 − λ 20 20 25 − λ ∣ = ( 25 − λ ) 2 − 400 = ( λ − 45 ) ( λ − 5 ) = 0 begin{vmatrix}25-lambda & 20\ 20 & 25-lambdaend{vmatrix}=(25-lambda)^2-400=(lambda-45)(lambda-5)=0 ∣∣∣∣25−λ202025−λ∣∣∣∣=(25−λ)2−400=(λ−45)(λ−5)=0
解 得 : λ 1 = 45 , λ 2 = 5 解得:lambda_1=45,lambda_2=5 解得:λ1=45,λ2=5
由 σ i = λ i , 得 到 奇 异 值 : σ 1 = 45 , σ 2 = 5 由sigma_i=sqrt{lambda_i},得到奇异值:sigma_1=sqrt{45},sigma_2=sqrt{5} 由σi=λi,得到奇异值:σ1=45,σ2=5 -
计算 A A T AA^T AAT的特征值和特征向量
求 得 : λ 1 = 45 , λ 2 = 5 ; v 1 = [ 1 2 1 2 ] ; v 2 = [ − 1 2 1 2 ] 求得:lambda_1=45,lambda_2=5; v_1=begin{bmatrix}frac{1}{sqrt{2}} \ frac{1}{sqrt{2}}end{bmatrix}; v_2=begin{bmatrix}-frac{1}{sqrt{2}} \ frac{1}{sqrt{2}}end{bmatrix} 求得:λ1=45,λ2=5; v1=[2121]; v2=[−2121] -
求奇异值
利 用 A v i = σ i u i , i = 1 , 2 , 求 奇 异 值 : 利用Av_i=sigma_iu_i,i=1,2,求奇异值: 利用Avi=σiui,i=1,2,求奇异值:
A v 1 = [ 3 2 9 2 ] = 45 [ 1 10 3 10 ] = σ 1 u 1 ; A v 2 = [ − 3 2 1 2 ] = 5 [ − 3 10 1 10 ] = σ 2 u 2 Av_1=begin{bmatrix}frac{3}{sqrt{2}} \ frac{9}{sqrt{2}}end{bmatrix}=sqrt{45}begin{bmatrix}frac{1}{sqrt{10}} \ frac{3}{sqrt{10}}end{bmatrix}=sigma_1u_1; Av_2=begin{bmatrix}-frac{3}{sqrt{2}} \ frac{1}{sqrt{2}}end{bmatrix}=sqrt{5}begin{bmatrix}-frac{3}{sqrt{10}} \ frac{1}{sqrt{10}}end{bmatrix}=sigma_2u_2 Av1=[2329]=45[101103]=σ1u1;Av2=[−2321]=5[−103101]=σ2u2 -
奇异值分解结果
U = [ 1 10 − 3 10 3 10 1 10 ] ; Σ = [ 45 0 0 5 ] ; V = [ 1 2 − 1 2 1 2 1 2 ] A = U Σ V T = [ 1 10 − 3 10 3 10 1 10 ] [ 45 0 0 5 ] [ 1 2 − 1 2 1 2 1 2 ] T = [ 3 0 4 5 ] begin{aligned} &U=begin{bmatrix}frac{1}{sqrt{10}} & -frac{3}{sqrt{10}} \ frac{3}{sqrt{10}} & frac{1}{sqrt{10}}end{bmatrix}; Sigma=begin{bmatrix}sqrt{45} & 0 \ 0 & sqrt{5}end{bmatrix}; V=begin{bmatrix}frac{1}{sqrt{2}} & -frac{1}{sqrt{2}} \ frac{1}{sqrt{2}} & frac{1}{sqrt{2}}end{bmatrix}\ &A=USigma{V^T}= begin{bmatrix}frac{1}{sqrt{10}} & -frac{3}{sqrt{10}} \ frac{3}{sqrt{10}} & frac{1}{sqrt{10}}end{bmatrix} begin{bmatrix}sqrt{45} & 0 \ 0 & sqrt{5}end{bmatrix} begin{bmatrix}frac{1}{sqrt{2}} & -frac{1}{sqrt{2}} \ frac{1}{sqrt{2}} & frac{1}{sqrt{2}}end{bmatrix}^T=begin{bmatrix}3 & 0 \ 4 & 5end{bmatrix} end{aligned} U=[101103−103101]; Σ=[45005]; V=[2121−2121]A=UΣVT=[101103−103101][45005][2121−2121]T=[3405]
2.4 奇异值分解近似
- SVD分解将一个矩阵进行分解,对角矩阵对角线上的特征值递减存放,奇异值的减少特别快;
- 对于奇异值,可以用最大的
k
k
k个奇异值和对应的左右奇异向量来近似描述矩阵;
A m × n = U m × m Σ m × n V n × n T ≈ U m × k Σ k × k V k × n T ; k 要 比 n 小 很 多 , 即 一 个 大 矩 阵 A 可 以 用 三 个 小 矩 阵 U m × k 、 Σ k × k 、 V k × n T 表 示 ; begin{aligned} & A_{mtimes{n}}=U_{mtimes{m}}Sigma_{mtimes{n}}V_{ntimes{n}}^T≈U_{mtimes{k}}Sigma_{ktimes{k}}V_{ktimes{n}}^T;\ k要比n小很多,即一个大矩阵A可以用&三个小矩阵U_{mtimes{k}}、Sigma_{ktimes{k}}、V_{ktimes{n}}^T表示; end{aligned} k要比n小很多,即一个大矩阵A可以用Am×n=Um×mΣm×nVn×nT≈Um×kΣk×kVk×nT;三个小矩阵Um×k、Σk×k、Vk×nT表示;
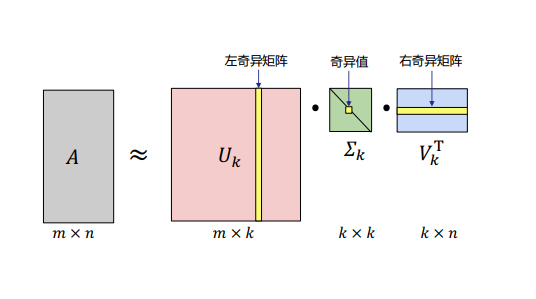
2.5 SVD案例

3.主成分分析(PCA)
3.1 PCA简述
- 主成分分析:Principal Component Analysis,PCA;
- 主成分分析:一种降维方法,通过将一个大的特征集转换成一个较小的特征集,小特征集仍包含原始数据中的大部分信息,从而降低了原始数据的维数;
- 减少一个数据集的特征数量,会牺牲一点准确性;
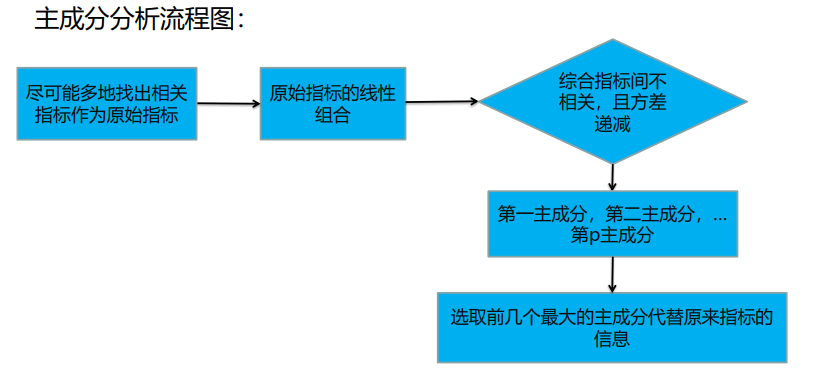
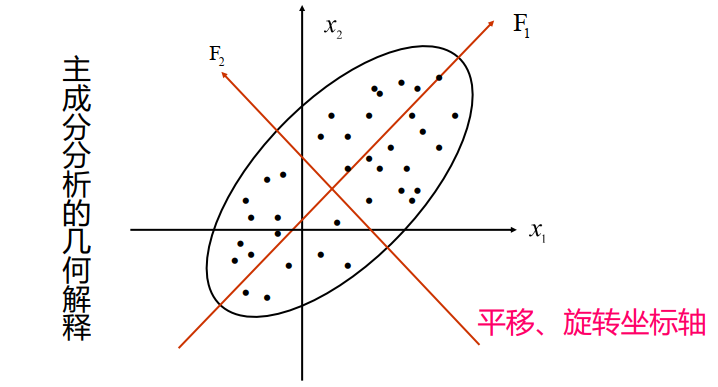
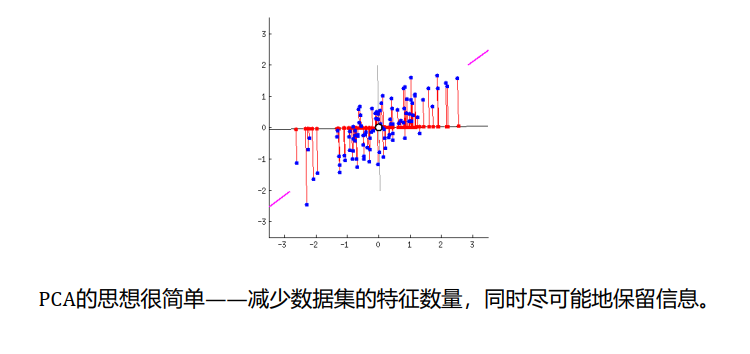
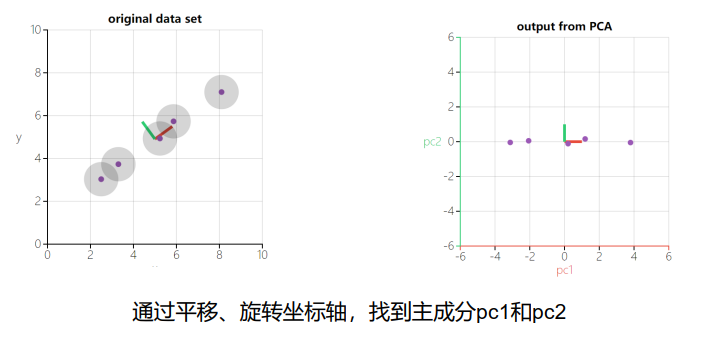
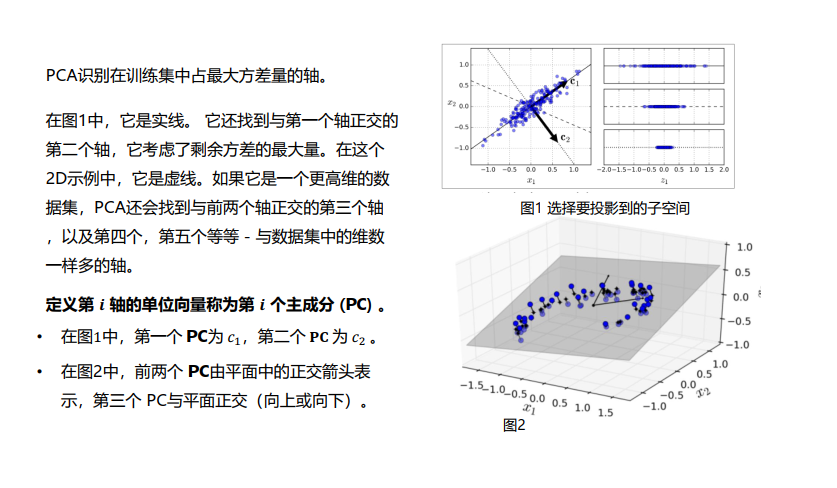
3.2 得到包含最大差异性的主成分方向的方法
- 通过计算数据矩阵的协方差矩阵;
- 得到协方差矩阵的特征值特征向量;
- 选择特征值最大的 k k k个特征所对应的特征向量组成的矩阵;
- 将数据矩阵转换到新的空间中,实现数据特征的降维;
3.3 PCA算法的实现方法
- 基于SVD分解协方差矩阵实现PCA算法;
- 基于特征值分解协方差矩阵实现PCA算法;
3.4 基于SVD分解协方差矩阵实现PCA算法
- 背景:PCA从 n n n维减少到 k k k维,设有 m m m条 n n n维数据,将原始数据按列组成 n n n行 m m m列矩阵 X X X
- 均值归一化。计算所有特征的均值,令 x j = x j − μ j ( μ j x_j=x_j-mu_j(mu_j xj=xj−μj(μj为均值 ) ) ),如果特征在不同数量级上,需要除以标准差 σ 2 sigma^2 σ2;
- 计算协方差矩阵 ( c o v a r i a n c e m a t r i x ) Σ (covariance matrix)Sigma (covariance matrix)Σ,即: Σ = 1 m ∑ i = 1 n ( x ( i ) ) ( x ( i ) ) T Sigma=frac{1}{m}sum_{i=1}^n(x^{(i)})(x^{(i)})^T Σ=m1∑i=1n(x(i))(x(i))T;
- 计算协方差矩阵
Σ
Sigma
Σ的特征向量
(
e
i
g
e
n
v
e
c
t
o
r
s
)
(eigenvectors)
(eigenvectors),利用奇异值分解来求解;
3.5 基于特征值分解协方差矩阵实现PCA算法
-
基础知识:
- 特征值与特征向量
如 果 一 个 向 量 v 是 矩 阵 A 的 特 征 向 量 , 则 满 足 : A v = λ v ; 其 中 : λ 是 特 征 向 量 A 对 应 的 特 征 值 , 一 个 矩 阵 的 一 组 特 征 向 量 是 一 组 正 交 向 量 ; 如果一个向量v是矩阵A的特征向量,则满足:Av=lambda{v};\ 其中:lambda是特征向量A对应的特征值,一个矩阵的一组特征向量是一组正交向量; 如果一个向量v是矩阵A的特征向量,则满足:Av=λv;其中:λ是特征向量A对应的特征值,一个矩阵的一组特征向量是一组正交向量; - 特征值分解矩阵
对 于 矩 阵 A , 有 一 组 特 征 向 量 v , 将 这 组 向 量 进 行 单 位 正 交 化 , 即 得 到 一 组 正 交 单 位 向 量 ; 特 征 值 分 解 , 将 矩 阵 A 分 解 为 : A = P Σ P − 1 ; 其 中 : P 是 矩 阵 A 的 特 征 向 量 组 成 的 矩 阵 ; Σ 是 一 个 对 角 阵 , 对 角 线 上 的 元 素 是 特 征 值 ; 对于矩阵A,有一组特征向量v,将这组向量进行单位正交化,即得到一组正交单位向量;\ 特征值分解,将矩阵A分解为:A=PSigma{P^{-1}};\ 其中:\ P是矩阵A的特征向量组成的矩阵;\ Sigma是一个对角阵,对角线上的元素是特征值; 对于矩阵A,有一组特征向量v,将这组向量进行单位正交化,即得到一组正交单位向量;特征值分解,将矩阵A分解为:A=PΣP−1;其中:P是矩阵A的特征向量组成的矩阵;Σ是一个对角阵,对角线上的元素是特征值;
- 特征值与特征向量
-
算法流程:
设有 m m m条 n n n维数据,将原始数据按列组成 n n n行 m m m列矩阵 X X X;- 均值归一化。计算所有特征的均值,令 x j = x j − μ j ( μ j x_j=x_j-mu_j(mu_j xj=xj−μj(μj为均值 ) ) ),如果特征在不同数量级上,需要除以标准差 σ 2 sigma^2 σ2;
- 计算协方差矩阵(covariance matrix) Σ Sigma Σ,即: Σ = 1 m ∑ i = 1 n ( x ( i ) ) ( x ( i ) ) T Sigma=frac{1}{m}sum_{i=1}^n(x^{(i)})(x^{(i)})^T Σ=m1∑i=1n(x(i))(x(i))T;
- 用特征值分解方法计算协方差矩阵 Σ Sigma Σ的特征值和特征向量;
- 对特征值从大到小排序,选择最大的 k k k个,将其对应的 k k k个特征向量分别作为行向量组成特征向量矩阵 P P P;
- 将数据转换到 k k k个特征向量构建的新空间中,即 Y = P X Y=PX Y=PX;
3.6 PCA算法案例分析
- 实例背景:
A = [ − 1 − 1 0 2 0 − 2 0 0 1 2 ] A=begin{bmatrix}-1 & -1 & 0 & 2 &0 \ -2 & 0 & 0 & 1 & 2end{bmatrix} A=[−1−2−10002102] - 矩阵每行为零均值;
- 求解协方差矩阵:
Σ = 1 5 [ − 1 − 1 0 2 0 − 2 0 0 1 2 ] [ − 1 − 2 − 1 0 0 0 2 1 0 1 ] = [ 6 5 4 5 4 5 6 5 ] Sigma=frac{1}{5}begin{bmatrix}-1 & -1 & 0 & 2 &0 \ -2 & 0 & 0 & 1 & 2end{bmatrix} begin{bmatrix}-1 & -2 \ -1 & 0 \ 0 & 0 \ 2 & 1 \ 0 & 1end{bmatrix}=begin{bmatrix}frac{6}{5} & frac{4}{5} \ frac{4}{5} & frac{6}{5}end{bmatrix} Σ=51[−1−2−10002102]⎣⎢⎢⎢⎢⎡−1−1020−20011⎦⎥⎥⎥⎥⎤=[56545456] - 求
Σ
Sigma
Σ的特征值和特征向量
∣ A − λ E ∣ = ∣ 6 5 − λ 4 5 4 5 6 5 − λ ∣ = ( 6 5 − λ ) 2 − 16 25 = 0 解 得 特 征 值 和 特 征 向 量 : λ 1 = 2 , λ 2 = 2 / 5 ; Σ 1 = [ 1 1 ] T , Σ 2 = [ − 1 1 ] T begin{aligned} &|A-lambda{E}|=begin{vmatrix}frac{6}{5}-lambda & frac{4}{5} \ frac{4}{5} & frac{6}{5}-lambdaend{vmatrix}=(frac{6}{5}-lambda)^2-frac{16}{25}=0\ &解得特征值和特征向量:lambda_1=2,lambda_2=2/5; Sigma_1=begin{bmatrix}1 & 1end{bmatrix}^T,Sigma_2=begin{bmatrix}-1 & 1end{bmatrix}^T end{aligned} ∣A−λE∣=∣∣∣∣56−λ545456−λ∣∣∣∣=(56−λ)2−2516=0解得特征值和特征向量:λ1=2,λ2=2/5; Σ1=[11]T,Σ2=[−11]T - 标准化后的特征向量
α 1 = [ 1 2 1 2 ] T , α 2 = [ − 1 2 1 2 ] T alpha_1=begin{bmatrix}frac{1}{sqrt{2}} & frac{1}{sqrt{2}}end{bmatrix}^T,alpha_2=begin{bmatrix}-frac{1}{sqrt{2}} & frac{1}{sqrt{2}}end{bmatrix}^T α1=[2121]T,α2=[−2121]T - 求得矩阵
P
P
P
P = [ 1 2 1 2 − 1 2 1 2 ] P=begin{bmatrix}frac{1}{sqrt{2}} & frac{1}{sqrt{2}} \ -frac{1}{sqrt{2}} & frac{1}{sqrt{2}}end{bmatrix} P=[21−212121] - 验证协方差矩阵
Σ
Sigma
Σ的对角化
P Σ P T = [ 1 2 1 2 − 1 2 1 2 ] [ 6 5 4 5 4 5 6 5 ] [ 1 2 − 1 2 1 2 1 2 ] = [ 2 0 0 2 5 ] PSigma{P^T}=begin{bmatrix}frac{1}{sqrt{2}} & frac{1}{sqrt{2}} \ -frac{1}{sqrt{2}} & frac{1}{sqrt{2}}end{bmatrix} begin{bmatrix}frac{6}{5} & frac{4}{5} \ frac{4}{5} & frac{6}{5}end{bmatrix} begin{bmatrix}frac{1}{sqrt{2}} & -frac{1}{sqrt{2}} \ frac{1}{sqrt{2}} & frac{1}{sqrt{2}}end{bmatrix}=begin{bmatrix}2 & 0 \ 0 & frac{2}{5}end{bmatrix} PΣPT=[21−212121][56545456][2121−2121]=[20052] - 降维后数据
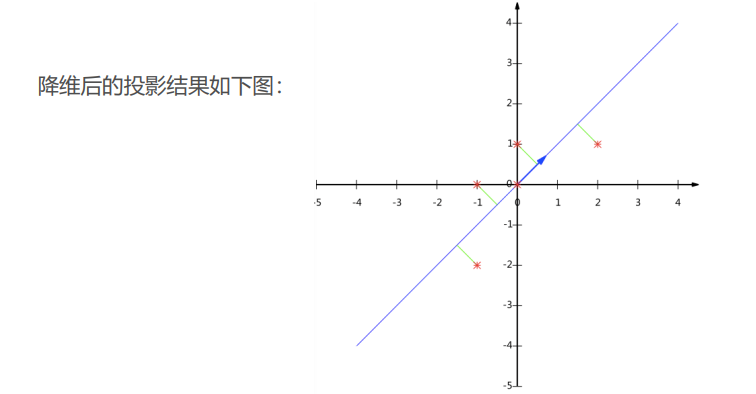
用 P 的 第 一 行 乘 以 数 据 矩 阵 , 得 到 降 维 后 数 据 表 示 : 用P的第一行乘以数据矩阵,得到降维后数据表示: 用P的第一行乘以数据矩阵,得到降维后数据表示:
Y = [ 1 2 1 2 ] [ − 1 − 1 0 2 0 − 2 0 0 1 1 ] = [ − 3 2 − 1 2 0 3 2 − 1 2 ] Y=begin{bmatrix}frac{1}{sqrt{2}} & frac{1}{sqrt{2}}end{bmatrix} begin{bmatrix}-1 & -1 & 0 & 2 & 0 \ -2 & 0 & 0 & 1 & 1end{bmatrix}= begin{bmatrix}-frac{3}{sqrt{2}} & -frac{1}{sqrt{2}} & 0 & frac{3}{sqrt{2}} & -frac{1}{sqrt{2}}end{bmatrix} Y=[2121][−1−2−10002101]=[−23−21023−21]
3.7 PCA算法优缺点
-
优点:
- 只需要以方差衡量信息量,不受数据集以外的因素影响;
- 各主成分之间正交,可消除原始数据成分之间的相互影响的因素;
- 计算方法简单,主要运算时特征值分解,易于实现;
- 无监督学习的一种,无参数限制;
-
缺点:
- 主成分各个特征维度的含义具有一定的模糊性,不如原始样本特征的解释性强;
- 方差小的非主成分可能包含对样本差异的重要信息,因降维丢弃可能对后续数据处理有影响;
注:矩阵分解部分不熟悉的读者需要详细阅读线性代数部分。
最后
以上就是端庄山水最近收集整理的关于机器学习入门14--降维的全部内容,更多相关机器学习入门14--降维内容请搜索靠谱客的其他文章。








发表评论 取消回复