相似变换Main.mOpenCV和Matlab

Main.m

% headpose_with_block/ini_shape
clc;clearvars;close all;
data=load('../data_temp/data.mat','data');
data=data.data;

meanshape=calc_meanshape2(data);
ind=1;
img=imread(data{ind}.imgPath);%color image
landmark=data{ind}.landmark;%landmark 10*2,其中landmark的坐标是相对于box的偏移
nlandmark=size(landmark,1);% n=10
box=data{ind}.bbox;%[x y w h]
figure(1);
subplot(1,2,1);
imshow(img);
title('原图像');
hold on;
for i=1:nlandmark
    plot(landmark(i,1)+box(1),landmark(i,2)+box(2),'.r','markersize',15);
end

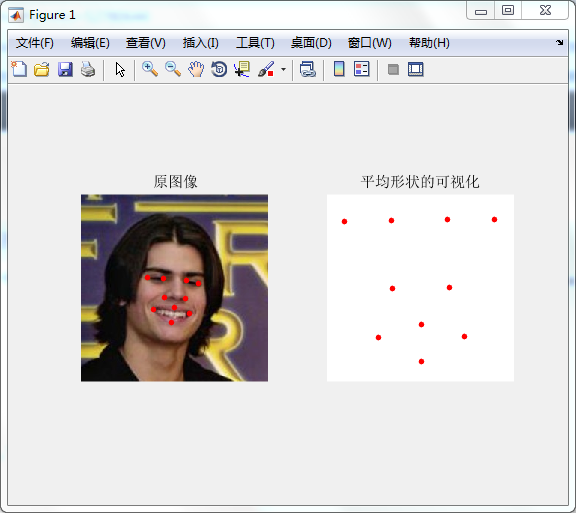
%显示平均形状

minxy=min(meanshape,[],1);
maxxy=max(meanshape,[],1);
shape=meanshape.*80+10;%尺度扩大80，+10是为平移到中间位置

img2=255*ones(100,100,3);
subplot(1,2,2);
imshow(img2);
title('平均形状的可视化');
hold on;
for i=1:nlandmark
    plot(shape(i,1),shape(i,2),'.r','markersize',15);
end

%% 计算相似变换
%%计算两个中心化的形状之间的相似变换
meanxy=mean(landmark,1);%landmark的中心
mean_shapexy=mean(meanshape,1);%meanshape的中心
 temp1=bsxfun(@minus,landmark,meanxy);
 temp2=bsxfun(@minus,meanshape,mean_shapexy).*100;%放置到100*100的标准框架中
 %from meanshape to landmark，计算相似变换矩阵
 %理论上,令T=trans_mat.T，T(3,1)=T(3,2)=0,即T中的tx=ty=0
trans_mat = fitgeotrans(bsxfun(@minus,meanshape,mean_shapexy).*100,bsxfun(@minus,landmark,meanxy), 'NonreflectiveSimilarity');

T=trans_mat.T;
wsize=[20 20];%目标的大小

T2=zeros(2,3);
T2(1,1)=T(1,1);
T2(1,2)=T(2,1);
T2(2,1)=T(1,2);
T2(2,2)=T(2,2);

T2(1,3)=landmark(1,1)+box(1)-(T2(1,1)*(wsize(1)-1)/2+T2(1,2)*(wsize(2)-1)/2);
T2(2,3)=landmark(1,2)+box(2)-(T2(2,1)*(wsize(1)-1)/2+T2(2,2)*(wsize(2)-1)/2);
%仿射逆变换，T2是从wsize窗口到图像中的仿射变换，其和trans_mat是统一的。
result=cv.warpAffine(img,T2,'DSize',wsize,'WarpInverse',1);
figure(2);
subplot(1,2,1);
imshow(img);
title('原图像');
hold on;
plot(landmark(1,1)+box(1),landmark(1,2)+box(2),'.r','markersize',15);
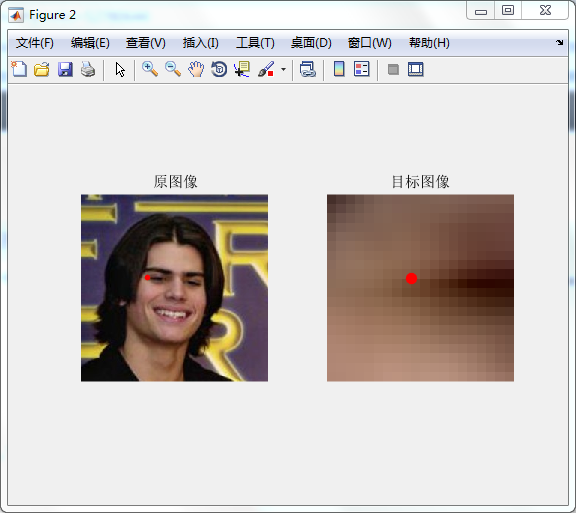
subplot(1,2,2);
imshow(result);
title('目标图像');
hold on;
plot((wsize(1)-1)/2,(wsize(2)-1)/2,'.r','markersize',30);

计算公式：

$$begin{equation} begin{aligned} begin{pmatrix} x'-x_i\ y'-y_i end{pmatrix}= begin{pmatrix} a_1 &a_2 \ b_1& b_2 end{pmatrix} begin{pmatrix} x-w_{cx}\ y-w_{cy} end{pmatrix} end{aligned} end{equation}$$
其中 $x_i=mathrm{landmark(1,1)},y_j=mathrm{landmark(1,2)}$, $x',y'$是关于图像img中的坐标， $x,y$是关于大小为wsize的目标图像中的坐标。 $w_{cx}和w_{cy}$表示目标图像的中心。
通过上面的公式，我们分离 $x',y',x,y$即可得到相似变换矩阵为：

$$begin{equation} begin{aligned} begin{pmatrix} x'\ y' end{pmatrix}= begin{pmatrix} a_1 &a_2&x_i-(a_1w_{cx}+a_2w_{cy}) \ b_1& b_2&y_i-(b_1w_{cx}+b_2w_{cy}) end{pmatrix} begin{pmatrix} x\ y \1 end{pmatrix} end{aligned} end{equation}$$

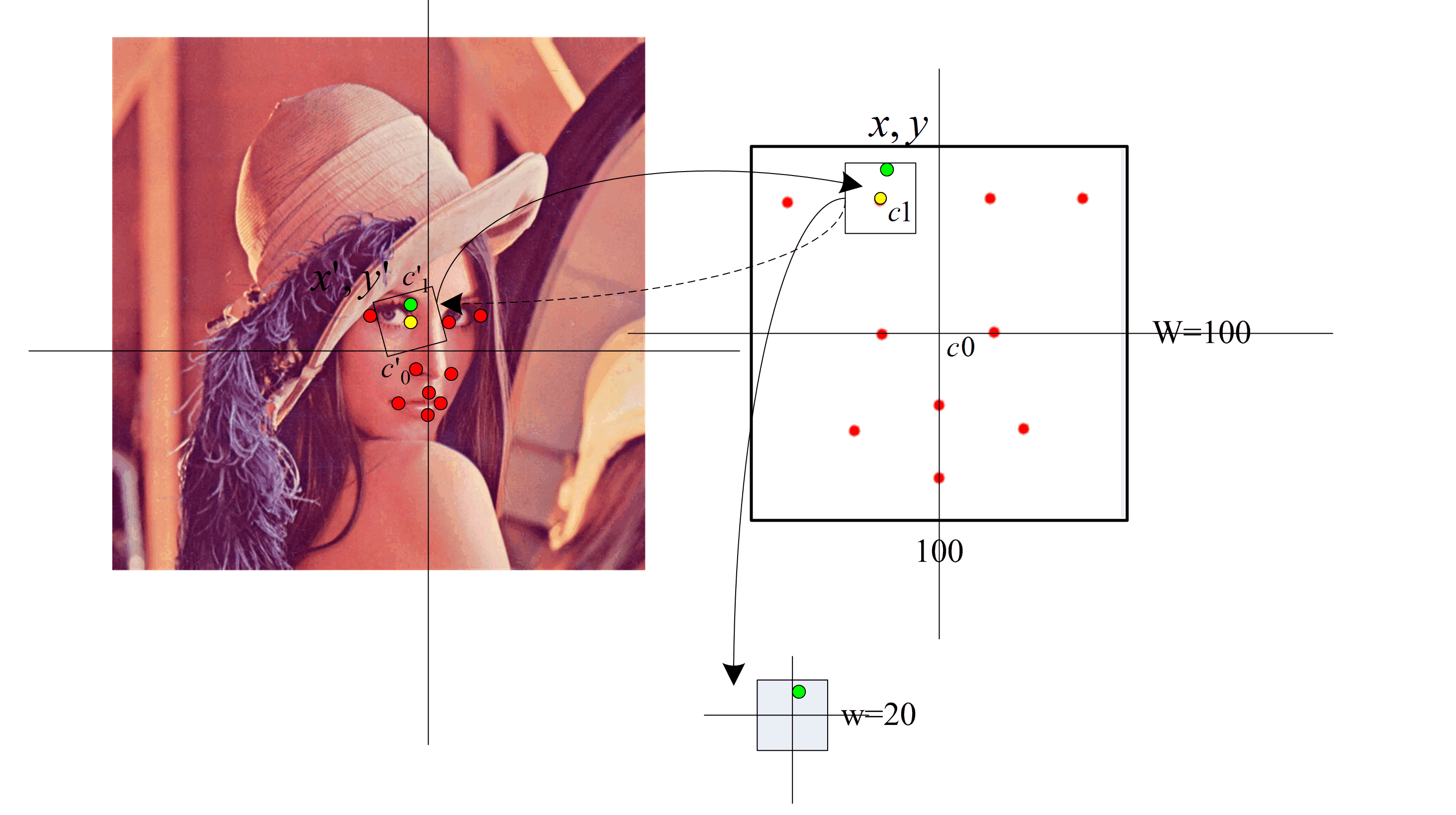
如上图，左右图像分别给出了坐标轴。左图：人脸图像给出了10个基准点，黄色的点是其中的一个基准点，绿色的点为以黄色点为中心的邻域内的一点。$c'_0$是10个基准点的重心（质心）,也是图中坐标系的原点。右图：给出了一个大小为100*100的框架，并将平均人脸映射到该框架内进行了可视化。同样的$c_0$是中心，$c_1$是其中的一个基准点。

假定左图像绿色点的坐标为$(x',y')$，右边图像绿色点的坐标为$(x,y)$

证明：

$$begin{equation} begin{aligned} begin{pmatrix} x'-x'_{c'0}\ y'-y'_{c'0} end{pmatrix}= begin{pmatrix} a_1 &a_2 \ b_1& b_2 end{pmatrix} begin{pmatrix} x-x_{c0}\ y-y_{c0} end{pmatrix} end{aligned} end{equation}$$
可以推出：
$$begin{equation} begin{aligned} begin{pmatrix} x'-x'_{c'1}\ y'-y'_{c'1} end{pmatrix}= begin{pmatrix} a_1 &a_2 \ b_1& b_2 end{pmatrix} begin{pmatrix} x-x_{c1}\ y-y_{c1} end{pmatrix} end{aligned} end{equation}$$
注释：隐含条件：
$$begin{equation} begin{aligned} begin{pmatrix} x'_{c'1}-x'_{c0}\ y'_{c'1}-y'_{c0} end{pmatrix}= begin{pmatrix} a_1 &a_2 \ b_1& b_2 end{pmatrix} begin{pmatrix} x_{c1}-x_{c0}\ y_{c1}-y_{c0} end{pmatrix} end{aligned} end{equation}$$

备注：因为上面是相似变换，因此满足:
$$a_1=b_2,a_2=-b_1$$

OpenCV和Matlab

OpenCV中计算形式为：

$$begin{equation} begin{aligned} begin{pmatrix} x'\ y' end{pmatrix}= begin{pmatrix} a &-b &t_x \ b& a &t_y end{pmatrix} begin{pmatrix} x\ y \1 end{pmatrix}= T_o begin{pmatrix} x\ y \1 end{pmatrix} end{aligned} end{equation}$$

Matlab中的计算形式为：

$$begin{equation} begin{aligned} begin{pmatrix} x' & y' end{pmatrix}= begin{pmatrix} x &y & 1 end{pmatrix} begin{pmatrix} a&b &0\ -b& a&0\t_x&t_y &1 end{pmatrix}= begin{pmatrix} x &y & 1 end{pmatrix} T_m end{aligned} end{equation}$$

最后

以上就是清秀身影为你收集整理的相似变换Main.mOpenCV和Matlab的全部内容，希望文章能够帮你解决相似变换Main.mOpenCV和Matlab所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。