汉罗塔问题和杨辉三角（java实现）汉罗塔杨辉三角

92 阅读 0 评论 61 点赞

我是靠谱客的博主贪玩冰淇淋，最近开发中收集的这篇文章主要介绍汉罗塔问题和杨辉三角（java实现）汉罗塔杨辉三角，觉得挺不错的，现在分享给大家，希望可以做个参考。

概述

汉罗塔问题和杨辉三角问题

汉罗塔
- - - 思路分析：
    - 代码：
杨辉三角
- - - 思路分析
    - 代码

汉罗塔

相传在古印度圣庙中，有一种被称为汉诺塔(Hanoi)的游戏。该游戏是在一块铜板装置上，有三根杆(编号A、B、C)，在A杆自下而上、由大到小按顺序放置n个金盘(如图1)。游戏的目标：把A杆上的金盘全部移到C杆上，并仍保持原有顺序叠好。操作规则：每次只能移动一个盘子，并且在移动过程中三根杆上都始终保持大盘在下，小盘在上，操作过程中盘子可以置于A、B、C任一杆上。

思路分析：

当只有一个盘子的时候：
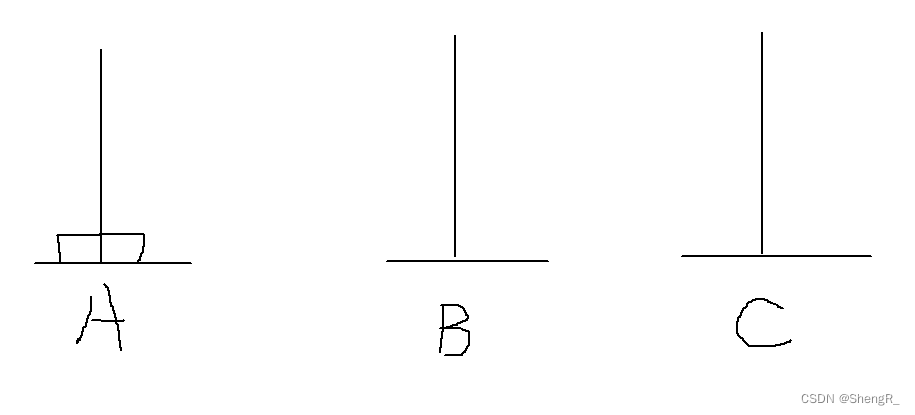
在这里插入图片描述
直接将A上的盘子放到C上即可
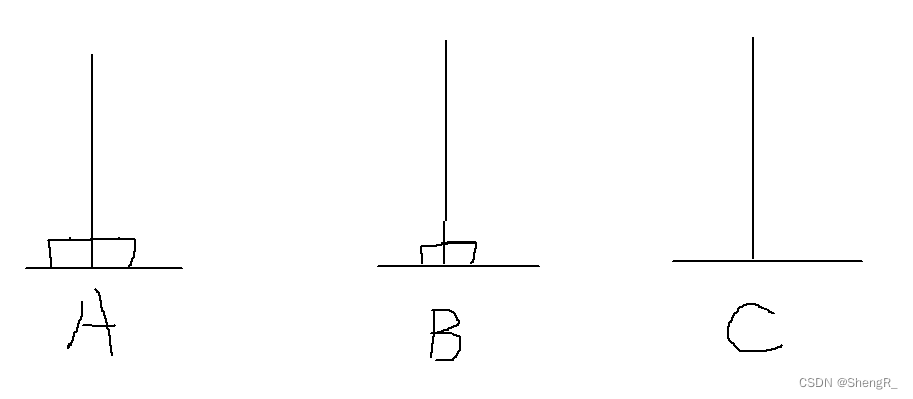
两个盘子的时候：
将A中第一个盘子放到B上，然后再将A上的最大的盘子放到C，最后将B上的盘子放到C上即可

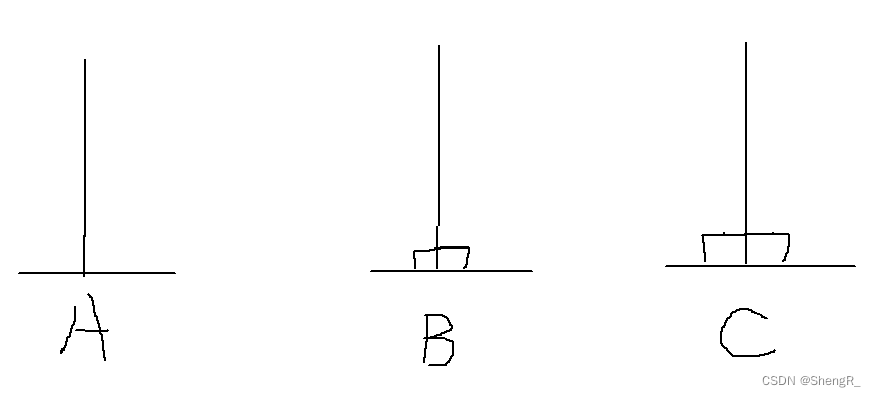
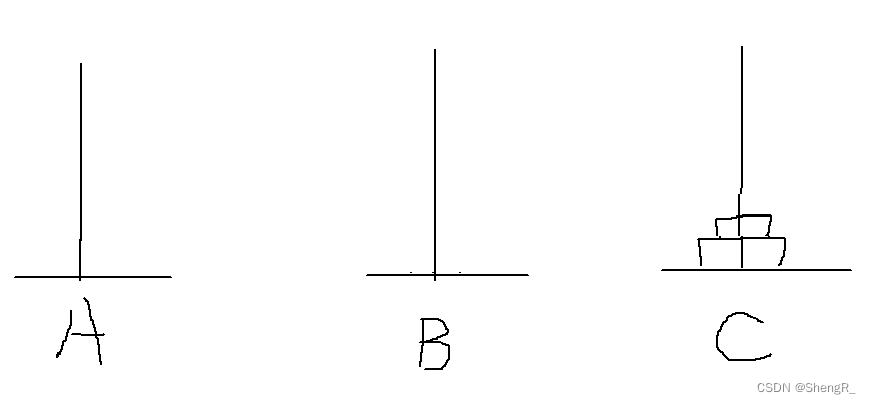
当三个盘子的时候：
A->C A->B C->B A->C B->A B->C A->C

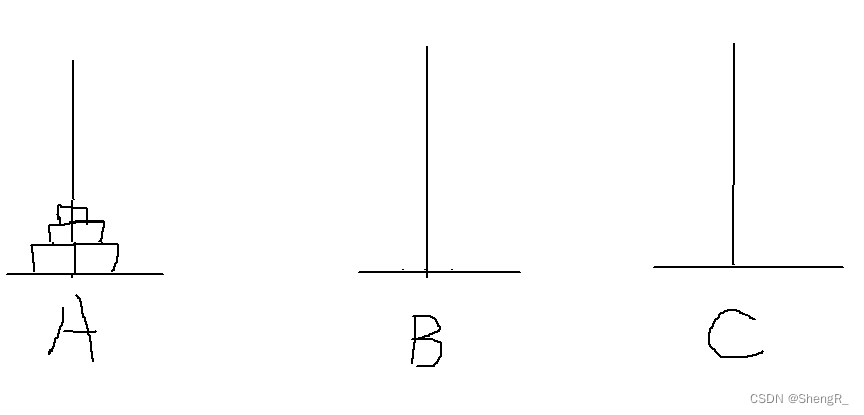
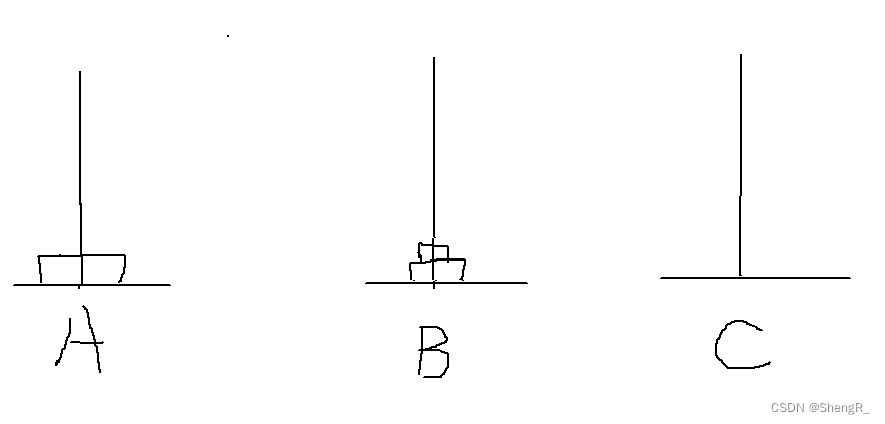
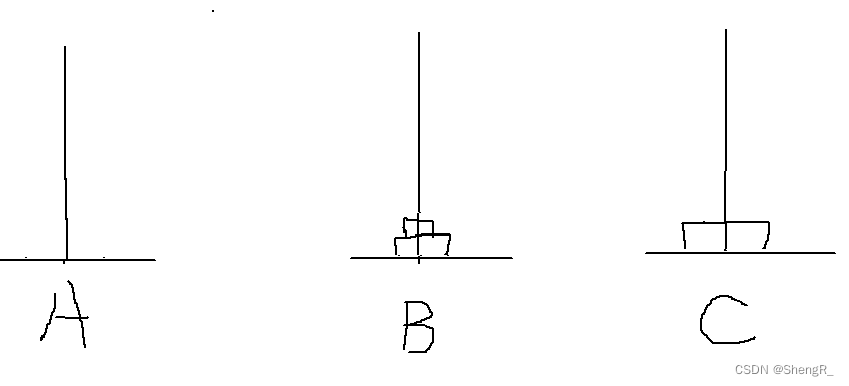
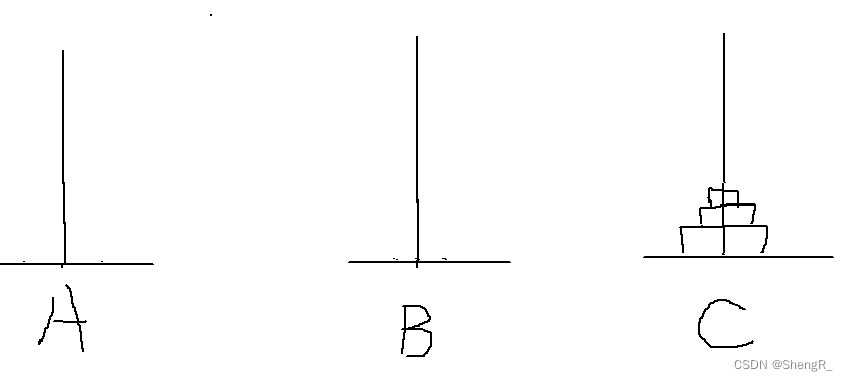
大体就是上面这几个步骤，其实可以发现，因为要求大的在下面，所以我A上的（n-1）个盘子必须移动到B上，然后C才能放最大的那个。然后再将B上的（n-1）个通过A再移动到C就可以了。
总结一下：就是当n大于1的时候，我们第一步需要把A上（n-1）个盘子通过C移动到B上，第二步就把A上的一个盘子移动到C上，第三步就可以将剩下的（n-1）个盘子通过A移动到C。这是每一次必做的步骤，且每一次都是这个步骤，若你再细想下去，B上的（n-1）个盘子，也是需要把（n-2）个盘子移动到A上，然后B再放到A，这里ABC不要想太死板，当B开始运那（n-1）个盘子的时候，B就是A。所以又回到了我们的第一步，所以可以用递归实现。

代码：

public class Text {
    //移动方法，代表从第一个形参移动到第二个形参，并非固定的A移动到C
    public static void move(char a,char c){
        System.out.print(a+"->"+c+" ");
    }
    //给定的abc三个参数代表最终我要的结果是从a通过b移动到c，并非固定的
    public static int work(int n,char a,char b,char c){
        //当汉罗塔层数为1时（n==1），直接从A放到C
        if(n == 1){
            move(a,c);
            //结束语
            return 0;
        }
        //当汉罗塔层数不为1时，首先第一步是将A中的（n-1）层通过C移动到B
        work(n-1,a,c,b);
        //现在的结果是A上有最大的一个，（n-1）个在B上，所以直接将A上的一个移动到C
        move(a,c);
        //上一步做完之后，B上的n-1个需要通过A移动到C
        work(n-1,b,a,c);
        //结束语
        return 0;
    }
    public static void main(String[] args) {
            System.out.println("请输入汉罗塔的层数:");
        Scanner scanner=new Scanner(System.in);
        int n = scanner.nextInt();
        //传入需要的层数和三个放置处
        work(n,'A','B','C');
    }
}

杨辉三角

杨辉三角，是二项式系数在三角形中的一种几何排列，中国南宋数学家杨辉1261年所著的《详解九章算法》一书中出现。在欧洲，帕斯卡（1623----1662）在1654年发现这一规律，所以这个表又叫做帕斯卡三角形。帕斯卡的发现比杨辉要迟393年，比贾宪迟600年。
在这里插入图片描述

思路分析

首先看图，它这样摆放我们是不好观察的，但是可以看出，第一排一个数字，第二排2个，第n排n个数字，所以这就可以结合二位数组来做。然后摆放规整后如下图
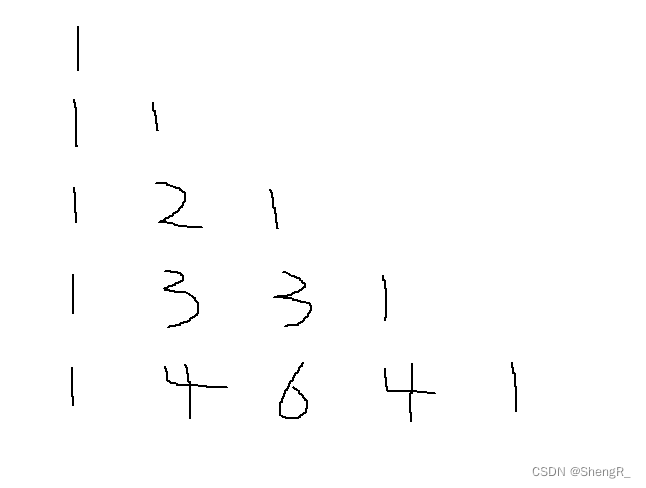
在这里插入图片描述
首先可以观察到每一排第一个和最后一个都是1，然后中间的值等于前一排前一列的加上前一排当前列的值。值确定了，数量呢？每一排比上一排多一个数，且是中间的数字，所以这里可以想到用for循环，分三个段，第一段赋值第一个数字，第二段对中间的数字进行赋值，这里不是一个数，所以需要用到for循环，第三段就是对最后一个数字进行赋值。最后将得到行的数据串在二维数组上即可。代码注释很详细，看代码。

代码

import java.util.ArrayList;
import java.util.List;
import java.util.Scanner;

public class Text2 {
    public static void main(String[] args) {
        System.out.println("输入N:");
        Scanner scanner=new Scanner(System.in);
        int n=scanner.nextInt();
        //二维数组，创建后增加的顺序可以想为向下，没增加一个，就多一行
        List<List<Integer>> arry=new ArrayList<>();
        //为每一行的值，添加到arry上面
        List<Integer> tem=new ArrayList<>();
        //先确定好第一排，因为每次都会需要前一排的数据，所以第一排得最先弄出来
        tem.add(1);
        arry.add(tem);
        for (int i = 1; i < n; i++) {
            //作为中介将数据串在二维数组上
            List<Integer> num=new ArrayList<>();
            //获取前一排的数据
            List<Integer> nu=arry.get(i-1);
            //第一步，确定第一个数字的值
            num.add(1);
            //第二步，对中间进行赋值
            for (int j = 1; j < i ; j++) {
                num.add(nu.get(j-1)+nu.get(j));
            }
            //第三步，确定最后一个数据
            num.add(1);
            //最后将得到的行串在最开始所创建的二维数组上
            arry.add(num);
        }
        System.out.println(arry);
    }
}