数据结构（C语言描述）优先队列

1 优先队列的定义

优先队列是一个以集合为基础的抽象数据类型。
优先队列中的每一个元素都有一个优先级。
定义在优先队列上的基本运算如下。
Min(H): 返回优先队列H中具有最下优先级的元素。
Insert(x,H): 将元素x插入优先队列H。
DeleteMin(H): 删除并返回优先队列H中具有最小优先级的元素。
在优先队列中，是按照每个对象的优先级顺序进行的。

2 优先队列的简单实现

所有实现字典的方法都可用于实现优先队列。优先队列中元素的优先级可以看成字典中元素的线性序值。
用有序链表实现优先队列，在O(1)时间内实现Min(H)和DeleteMin(H)运算，但Insert(x,H)运算在最坏情况下需要O(n)时间。n为插入元素时优先队列中已有的元素个数。
用二叉搜索树表示有n个元素的优先队列，在最坏情况下Insert(x,H)和DeleteMin(H)运算需要O(n)时间，在平均情况下需要O(logn)时间。
用无序链表实现优先队列，在O(1)时间内实现Insert(x,H)运算，但DeleteMin(H)运算却需要O(n)时间。

3 优先级树和堆

3.1 优先级树

对二叉搜索树进行适当修改，将二叉搜索性质换成下面的优先性质，从而引入优先级树。
优先级树的性质：
（1）树中每一结点存储一个元素。
（2）任一结点中存储的元素的优先级不大于其儿子结点中存储的元素的优先级。（优先级越小越往树根走）
较高层结点有较小优先级，这类优先级树称为极小化优先级树。
若在一棵优先级树中，任一结点中存储的元素的优先级不小于其儿子结点中存储的元素的优先级，则相应的优先级称为极大化优先级树。

3.2 堆

当一棵优先级树是近似满二叉树，称其为堆或偏序树。
极小化优先级树相应的堆称为极小化堆；极大化优先级树相应的堆称为极大化堆。
下图的优先级树是一个极小化堆。

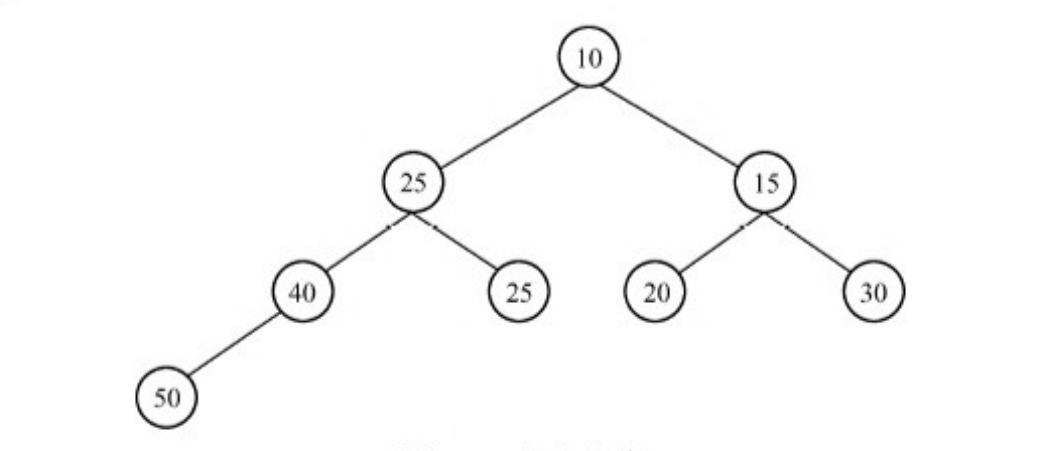
通常情况下，堆即指极小化堆；优先级树即指极小化优先级树。

3.2.1 堆的Delete(H)运算

思路：
（1）删去堆中最底层最右边的叶结点，该结点直接代替树根。
（2）该结点不断与它具有较小优先级的儿子交换位置，直到它的两个儿子的优先级都不小宇宇它的优先级或它已降到叶结点的位置为止。一句话优先级越大越往底层走。
例如：下图极小化堆执行Delete(H)运算

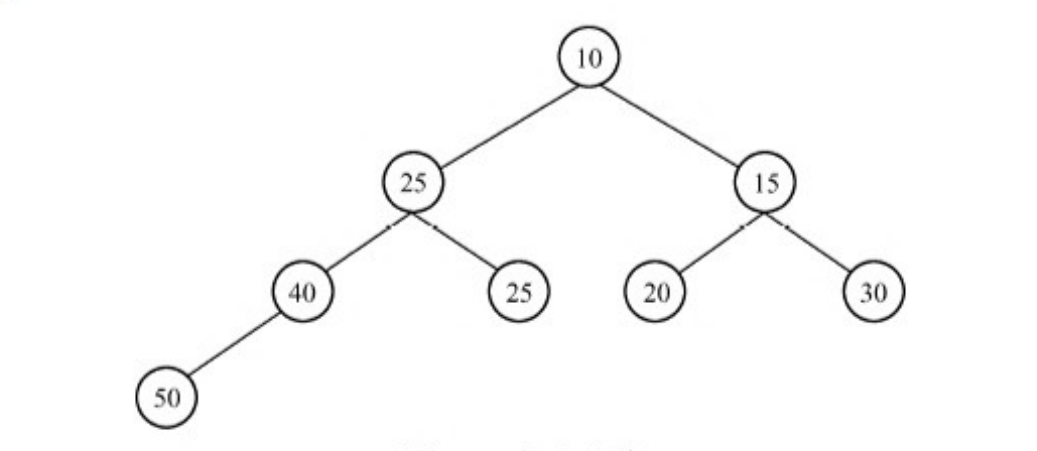
第一步，删去堆中最底层最右边的叶结点，该结点直接代替树根。

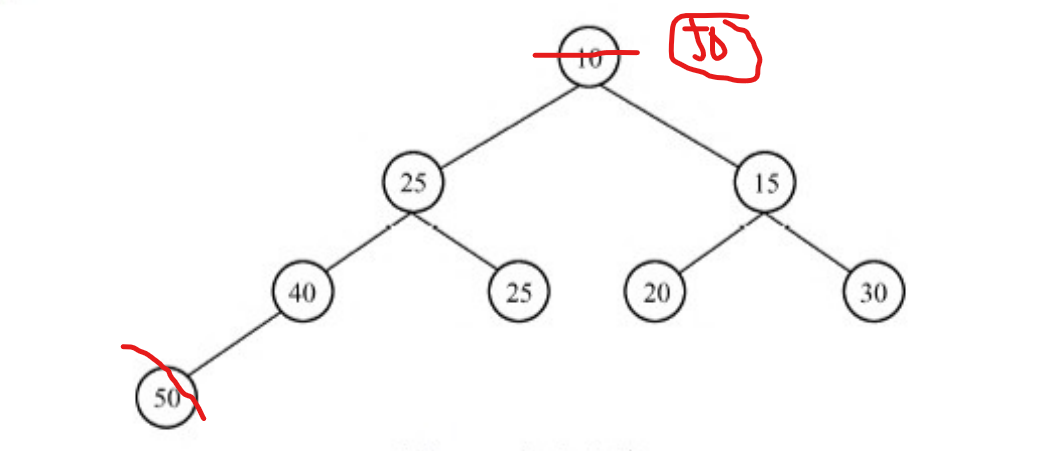
第二步，

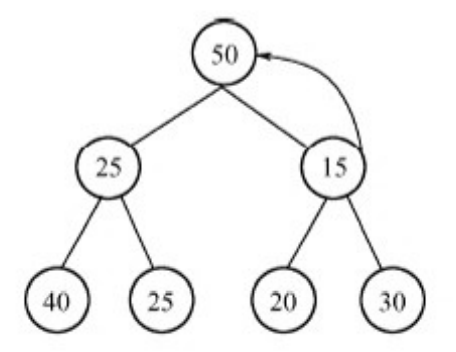
50的优先级大于15，所以50与15交换顺序。

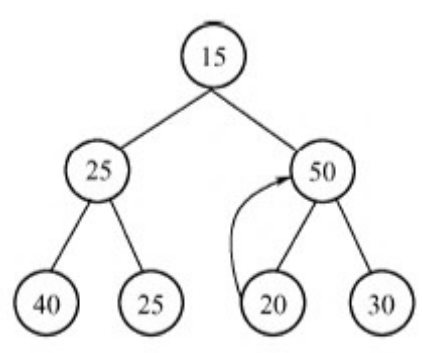
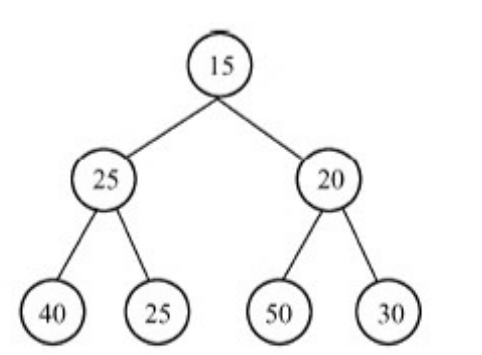
50的优先级大于20,50与20交换位置，50到叶结点位置，结束运算。

3.2.2 堆的Insert(x,H)运算

思路：
（1）将存放新元素的结点添加在堆的最底层。
（2）插入的元素的优先级小于其父结点中的元素的优先级，就交换他们的位置，直到新元素的优先级不小于其父结点中元素的优先级或已升到树根结点为止。一句话，优先级越小越往树根走。
Insert(x,H)运算在最坏情况下也只要O(logn)时间。
例如：在下图堆插入优先级为8的元素。

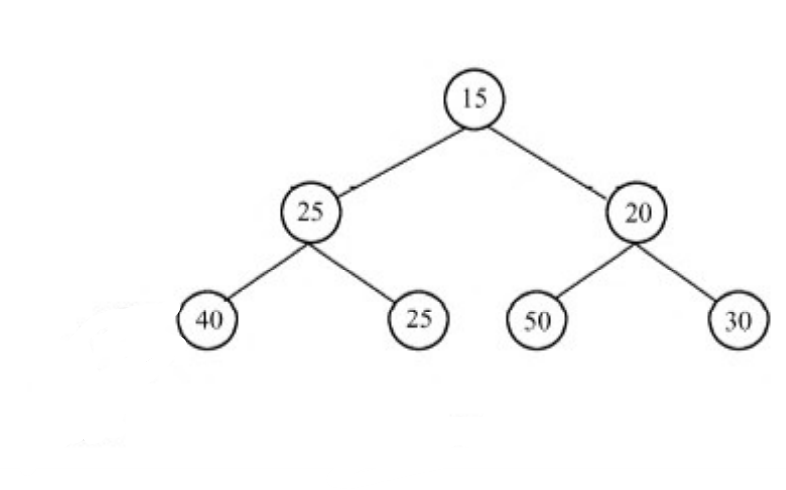
步骤：
（1）将插入元素添加到最底层

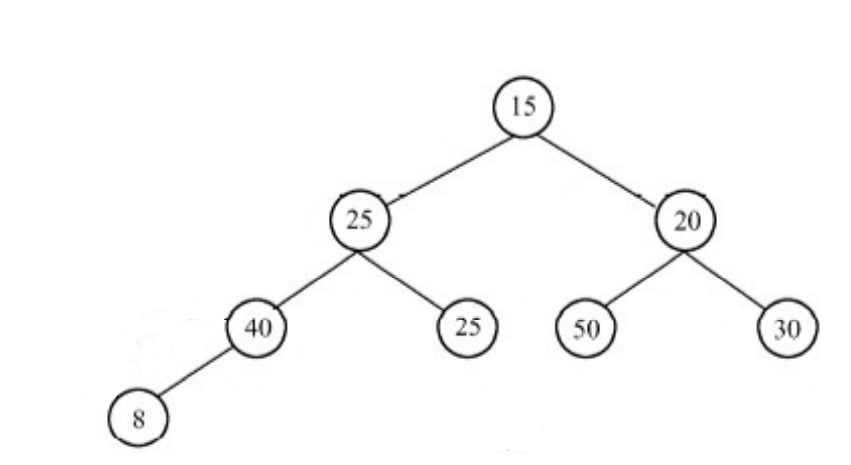
（2）优先级越小越往树根走


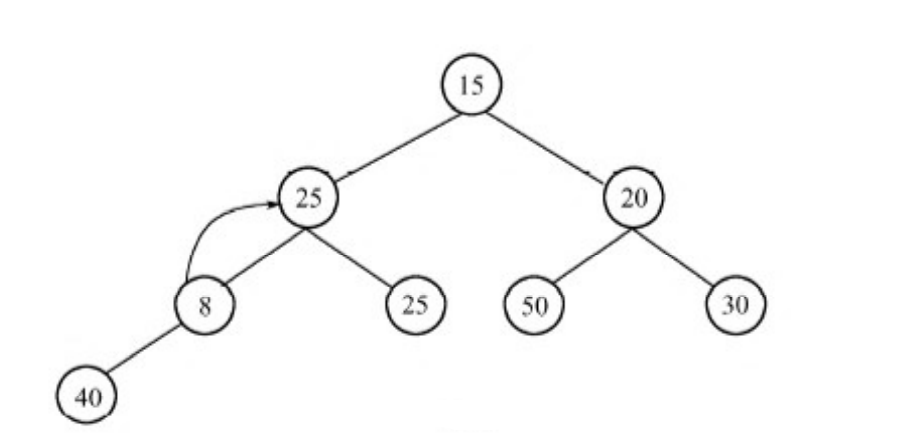
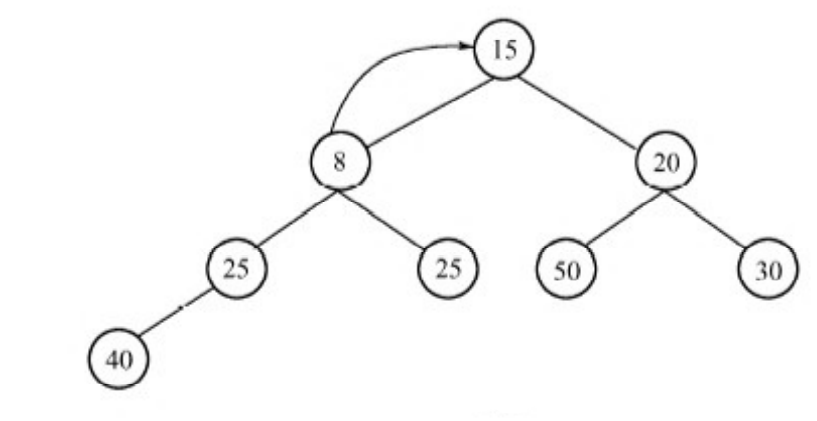
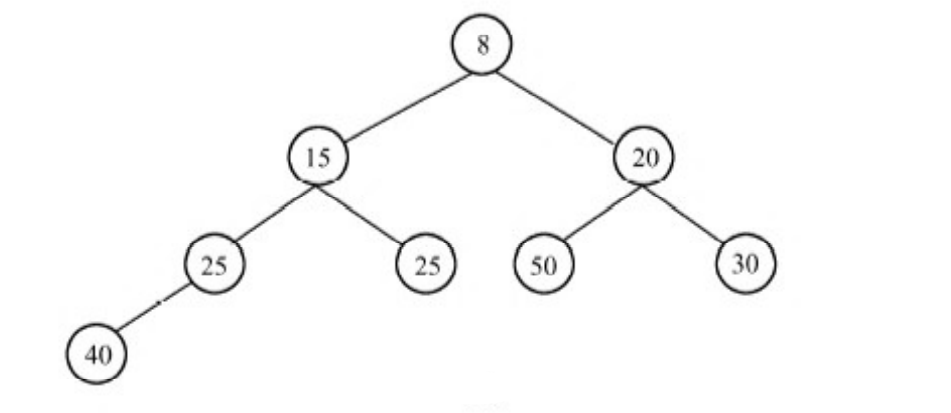
最后，该插入元素到达树根，运算结束。

4 用数组实现堆

4.1 基本概念及其定义

堆中元素按层序列表。
例如：下图堆

按层序遍历，得堆中元素在数组中的存储顺序为10 25 15 40 25 20 30 50
用数组实现的极小化堆Minheap的结构定义如下。

其中，heap是堆数组，用于存储堆中元素。maxsize是堆数组的最大长度。last是一个整数，它指示堆数组被优先队列中元素占用的最后一个单元的位置。

4.1 函数MinHeapInit(HeapSize)

函数MinHeapInit(HeapSize)创建一个空堆，其中堆数组的最大长度为HeapSize。

4.2 函数HeapInsert(x,H)

在堆H中插入一个元素x的算法HeapInsert(x,H)实现如下。

4.3 函数DeleteMin(H)

在堆H中抽取最小元的算法DeleteMin(H)描述如下。

4.4 函数BuildHeap(a,n,arraysize)

给定一个有n个元素的数组a，可用下面的算法BuildHeap(a,n,arraysize)在O(n)时间内将数组a调整为一个堆。


算法BuildHeap(a,n,arraysize)的计算时间是O(n)。

4.5 函数HeapSort(a,n)

利用上述堆结构进行排序的算法称为堆排序算法，它可在O(nlogn)时间内实现对给定数组a就地排序。

5 可并优先队列

可并优先队列是一个以集合为基础的抽象数据类型， 除必须支持优先队列的Insert和Delete Min运算外， 可并优先队列还支持两个不同优先队列的合并运算Concatenate。

5.1 左偏树的定义

左偏树是一类特殊的优先级树。左偏树有极小化左偏树与极大化左偏树之分。
左偏树分为左偏高树和左偏重树。
左偏高树，左子树偏高。左偏重树，左子树偏重。
对于二叉树中任意一个结点x，递归地定义其高度s(x)为

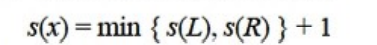
对于二叉树中任意一个结点x，递归地定义其重量s(x)为

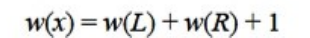
一棵优先级树是一棵左偏高树，当且仅当在该树的每个内结点处，其左儿子结点的高大于或等于其右儿子结点的高。
左偏高树性质：

一棵优先级树是一棵左偏重树，当且仅当在该树的每个内结点处，其左儿子结点的重大于或等于其右儿子结点的重。

5.2 用左偏树实现可并优先队列

5.2.1 函数NewHBLTnode(x,s)

左偏高树的结点类型HBLTNode说明如下。


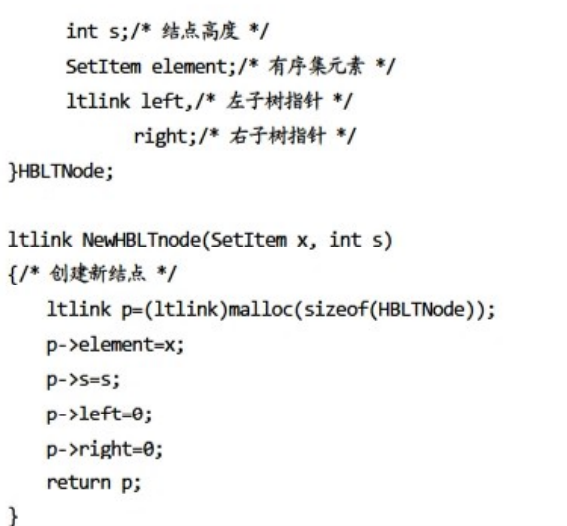
其中，clement存放优先队列中的元素；s保存当前结点的高度值；left和right分别指向左、右儿子结点的指针。
用左偏树实现的可并优先队列MinHBLT描述如下。

5.2.2 函数HBLTInit()

函数HBLTInit()将root置为空指针，创建一棵空树。

5.2.3 Concatenate(x,y)

左偏树的合并运算Concatenate(x,y)。它将两棵树分别以x和y为根的左偏树合并为一棵新的以x为根的左偏树。

算法Concatenate计算时间为O(logn)。

5.2.3 函数HBLTInsert(x,H)

要在左偏高树中插入一个元素x，可先创建存储元素x的单结点左偏高树，然后将新创建的单结点左偏高树与待插入的左偏高树合并即可。

5.2.4 函数HBLTMin(H)

HBLTMin(H)运算只要返回H的根结点中元素即可。

5.2.5 函数DeleteMin(H)

DeleteMin(H)运算删除H的根结点后，将根结点的左、右子树合并。

DeleteMin(H)所需的计算时间是O(logn)。

5.2.7 左偏高树的建树

左偏高树的建树运算用给定数组a中的n个元素创建一棵存储这n个元素的左偏高树。若用将元素逐次插入左偏高树的方法， 则需要O(n logn) 时间。下面的建树方法只需要O(n)时间。

上述算法先创建存储给n个元素的n棵单结点左偏高树，并将这n棵树存入一个队列Q中。然后依队列顺序逐次合并队首的两棵左偏高树，直到队列Q中只剩下一棵树时为止。

小结

主题是以集合为基础的抽象数据类型优先队列及其实现方法。
优先队列支持的主要集合运算是插入运算和删除最小元运算。由于优先队列与字典的相似性，所有实现字典的方法都可用于实现优先队列，但用优先级树和堆来实现优先队列效率更高。
介绍了用数组实现的极小化堆。当堆中有n个元素时，插入运算和删除最小元运算在最坏情况下所需的计算时间均为O(logn) 。
利用堆结构还可以设计出对给定的n个元素就地排序的堆排序算法。在最坏情况下， 堆排序算法只需要进行O(logn) 次元素键的比较。
可并优先队列也是以集合为基础的抽象数据类型。除必须支持优先队列的插入运算和删除最小元运算外，可并优先队列还支持两个不同优先队列的合并运算。
左偏树是实现可并优先队列的高效数据结构。对于含有n个元素的集合，左偏树可以在最坏情况下需要O(logn)时间完成可并优先队列支持的插入运算、删除最小元运算和两个不同优先队列的合并运算。

最后

以上就是酷酷纸鹤为你收集整理的数据结构（C语言描述）优先队列的全部内容，希望文章能够帮你解决数据结构（C语言描述）优先队列所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。