我们之前已经介绍过队列-C语言实现,它们是先入先出的,这很容易用平常的排队来理解。但是如果这个队列要支持有紧急情况的人先出队呢?原先那种队列就不再适用了,我们需要使用本文所提到的特殊队列—优先队列。本文相关代码地址 github 。
优先队列
优先队列也是一种抽象数据类型。优先队列中的每个元素都有优先级,而优先级高(或者低)的将会先出队,而优先级相同的则按照其在优先队列中的顺序依次出队。
也就是说优先队列,通常会有下面的操作:
将元素插入队列
将最大或者最小元素删除
这样的话,我们完全可以使用链表来实现,例如以O(1)复杂度插入,每次在表头插入,而以O(N)复杂度执行删除最小元素;或者以O(N)复杂度插入,保持链表有序,而以O(1)复杂度删除。
然而 优先队列往往使用堆来实现 ,以至于通常说堆时,就自然而然地想到了优先队列。
二叉堆
二叉树堆是一棵 完全二叉树 ,并且对于每一个节点(根节点除外),它的父节点小于或等于它,这样最小元素就会在堆顶,我们就很容易找到最小元素。如果你还不清楚二叉树,建议先阅读《二叉树-C语言实现》。为了理解二叉堆的特性,还需要再介绍两个概念:
满二叉树:除叶子节点外,所有节点都有两个子节点,称为满二叉树。这个很容易理解,就不多做解释。
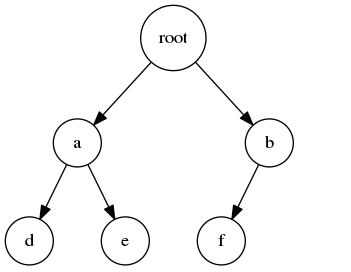
完全二叉树 :除了最后一层外,每层节点个数达到最大,并且最后一层的叶子节点都靠左边排列。
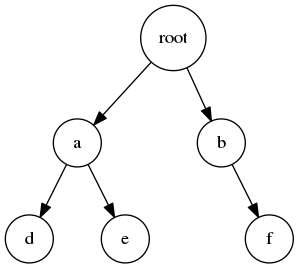
如下图一是一棵完全二叉树,而图二中的不是,因为最后一层的叶子节点不全在左边排列。
二叉堆可以很容易用数组来表示,因为一棵高度为h的完全二叉树有2^h到2^(h+1)-1个节点,这样存放一个二叉堆就不会太浪费空间,而且一旦知道高度,就可以知道节点数的范围。
那么如何使用数组来表示二叉堆怎么存放元素呢?
对于数组i上的元素,它的左儿子在2i位置,右儿子2i+1的位置,那么它的父节点在[i/2]的位置。例如节点1位置的左儿子节点在2处。
本文位置0不存储数据
例如,对于下面的二叉堆(用字母表示的二叉堆),如果存储在数组中,则是下面这样:
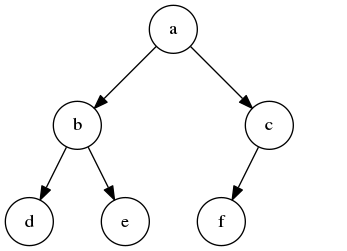
数组中存放情况:
0
1
2
3
4
5
6
不存储
a
b
c
d
e
f
二叉堆的操作
我们假设后面的操作都是让最小元素在堆顶,即对小堆操作。堆的常见操作有:
初始化
判断堆是否满
判断堆是否为空
向堆中插入元素
销毁堆
删除最小元素
找到最小元素
初始化堆
初始化堆之前,先定义堆结构。
typedef struct HeapStruct
{
int capacity; //最大元素数量
int size; //堆元素数量
ElementType *eles; //堆元素数组
}PriorityQueue;
这里定义了HeapStruct结构,包含三个元素,分别是最大容量,当前堆大小,以及堆数组。
因为这里使用的是动态数组,所以我们需要对其进行初始化,当然你也可以参考《如何自己实现一个栈》使用静态数组来实现,但这种方式的缺点很明显,它只能固定堆大小。
堆初始化函数如下:
PriorityQueue *init_PQ(int maxEleNum)
{
PriorityQueue *pq = NULL;
/*检查输入大小的合法性*/
if(maxEleNum <= 0 )
return NULL;
pq = malloc(sizeof(PriorityQueue));
if(NULL == pq)
{
printf("malloc failedn");
return NULL;
}
/*下标为0的位置保留,不作使用*/
pq->eles = malloc((maxEleNum + 1)*sizeof(ElementType));
if(NULL == pq->eles)
{
printf("malloc failedn");
free(pq);
return NULL;
}
/*初始化成员*/
memset(pq->eles,0,(maxEleNum + 1)*sizeof(ElementType));
pq->capacity = maxEleNum;
pq->size = 0;
return pq;
}
主要做了以下几件事:
创建一个空堆
初始化元素数量为0
堆是否已满
判断堆是否已满只需要判断容量和当前大小的比较结果即可:
int pq_is_full(PriorityQueue *pq)
{
if(NULL == pq)
return false;
if(pq->capacity == pq->size)
return true;
else
return false;
}
堆是否已空
判断堆是否为空只需要判断它的size是否为0即可:
int pq_is_empty(PriorityQueue *pq)
{
if(NULL == pq)
return false;
if(0 == pq->size)
return true;
else
return false;
}
堆的插入
按照我们前面的分析,插入操作是比较容易,放在属于它的下标位置即可,但是为了保持堆的性质,即节点的值要大于等于它的父节点,插入时就需要考虑更多了。
我们可以采取这样的方式:
将元素准备插入到下一个空闲位置(空穴)
如果插入后,仍然保持堆得性质,则直接插入该位置
如果插入后,导致父节点不再小于等于它,则将父节点值移到该空穴,父节点原来的位置就变成空穴
继续尝试将心得元素放入上面的空穴,并与父节点比较,知道新元素找到属于它的位置
举个例子,假如要在下面的二叉堆中,再插入2:
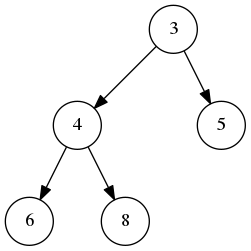
首先把2放在完全二叉树的最后一个位置,即前面提到的空闲位置,如下图:
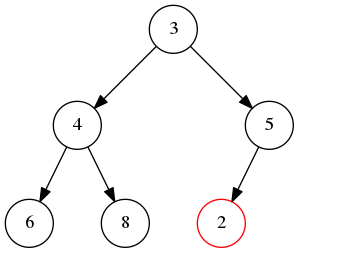
由于2比它的父节点5要小,如果插在这里,则不满足堆性质,因此,需要交换它和父节点的位置:
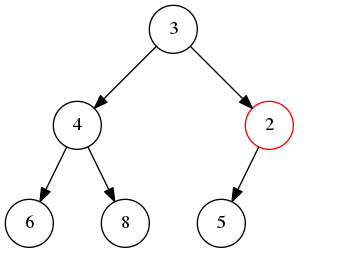
此时,发现2所在位置仍然比它的父节点要小,因此,还需要和它的父节点交换位置:
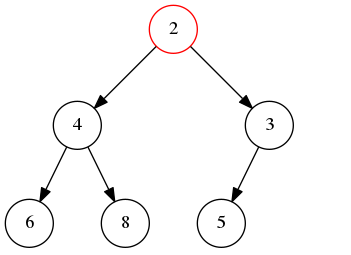
最终状态则满足堆得性质,即父节点总是小于等于它的子节点。
代码实现如下:
int insert_pq(ElementType value,PriorityQueue *pq)
{
int i =0;
/*确保优先队列没有满*/
if(pq_is_full(pq))
{
printf("priorityQueue is fulln");
return FAILURE;
}
printf("insert %dn",value);
/*不断和父节点探测比较,直到找到属于它的位置*/
for(i = pq->size+1;pq->eles[i/2] > value && i > 1;i/=2)
{
pq->eles[i] = pq->eles[i/2];
}
pq->eles[i] = value;
pq->size++;
return SUCCESS;
}
建立N个元素的二叉堆的时间复杂度为O(N)。
找到最小元素
由于我们在插入的时候就保证了堆的性质,因此找到最小元素是非常容易的,因为它就是位于堆顶,因此代码实现如下:
int find_min(PriorityQueue *pq,ElementType *value)
{
if(pq_is_empty(pq))
{
printf("priorityQueue is emptyn");
return FAILURE;
}
/*0处的元素作为哨兵没有使用*/
*value = pq->eles[1];
return SUCCESS;
}
删除最小元素
删除与插入相反,删除的是堆顶元素,我们需要找到一个元素来替代堆顶的位置,以保证堆的性质不被破坏。因此进行如下的操作:
删除堆顶元素,堆顶成为空穴
由于直接将最后的元素放入前面的空穴可能破坏堆性质,因此将较小的儿子插入空穴,该儿子的位置变成空穴,这样空穴就下滑了一层
重复上面的过程,空穴不能再下滑,将最后的元素放入该空穴
还是以前面建立的二叉堆为例,假如要删除堆顶的2。则直接先把2删除,那么2的位置就有一个空穴。
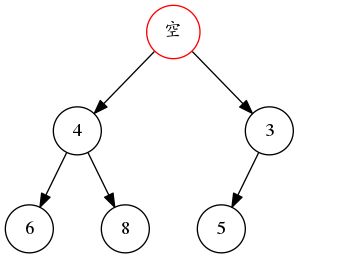
这个时候,我们将它的两个子节点中较小的一个,移动到堆顶位置:
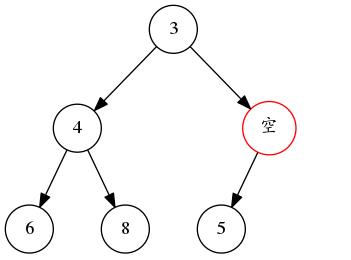
最后继续将空穴位置处它的子节点较小的一个,移动到空穴位置:
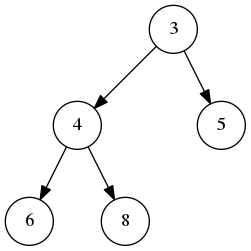
最终删除了堆顶元素。
代码实现如下:
int delete_min(PriorityQueue *pq,ElementType *min)
{
int i = 1;
int minChild =0;
if(pq_is_empty(pq))
{
printf("priorityqueue is emptyn");
return FAILURE;
}
/*取得最小值*/
*min = pq->eles[1];
/*暂时取出最后的元素*/
ElementType last = pq->eles[pq->size];
pq->size--;
if(0 == pq->size)
{
pq->eles[i] = 0;
return SUCCESS;
}
/*不断将空穴下滑*/
for(i = 1;i * 2 <= pq->size;i = minChild)
{
minChild = i * 2;
/*找到更小的孩子*/
if(minChild != pq->size && pq->eles[minChild+1] < pq->eles[minChild])
minChild+=1;
/*如果最后一个元素比空穴处的小儿子大,则继续下滑空穴,将该孩子上滤*/
if(last >pq->eles[minChild])
pq->eles[i] = pq->eles[minChild];
/*否则说明last放的位置不会破坏堆性质,则直接退出循环*/
else
break;
}
/*将最后的元素放在空穴位置*/
pq->eles[i] = last;
return SUCCESS;
}
删除操作的平均时间复杂度为O(logN)
完整代码运行结果
完整代码见开头说明的地址,运行结果如下:
insert 3
insert 4
insert 5
insert 6
insert 8
insert 2
priorityQueue is full
priorityQueue is full
the arr value is: 2 4 3 6 8 5
pq size is 6
the min is 2
the min is 3
the min is 4
the min is 5
the min is 6
the min is 8
destory pq success
观察删除最小元素的结果,有没有发现什么呢?
总结
本文介绍了优先队列最常见的实现方式-二叉堆实现,并且介绍了二叉堆地创建,插入和删除等基本操作。而典型的TOP k问题也非常适合使用堆来解决,本文不做介绍。
最后
以上就是欢呼彩虹最近收集整理的关于优先队列 c语言,优先队列-C语言实现的全部内容,更多相关优先队列内容请搜索靠谱客的其他文章。








发表评论 取消回复