day04 1113 红与黑（flood fill算法，即DFS，BFS）

78 阅读 0 评论 52 点赞

我是靠谱客的博主俊逸小懒虫，最近开发中收集的这篇文章主要介绍day04 1113 红与黑（flood fill算法，即DFS，BFS），觉得挺不错的，现在分享给大家，希望可以做个参考。

概述

1113 红与黑（Flood Fill算法，用DFS或BFS求解）

有一间长方形的房子，地上铺了红色、黑色两种颜色的正方形瓷砖。

你站在其中一块黑色的瓷砖上，只能向相邻（上下左右四个方向）的黑色瓷砖移动。

请写一个程序，计算你总共能够到达多少块黑色的瓷砖。

输入格式
输入包括多个数据集合。

每个数据集合的第一行是两个整数 $W$ 和 $H$ ，分别表示 $x$ 方向和 $y$ 方向瓷砖的数量。

在接下来的 $H$ 行中，每行包括 $W$ 个字符。每个字符表示一块瓷砖的颜色，规则如下

1）‘.’：黑色的瓷砖；
2）‘#’：红色的瓷砖；
3）‘@’：黑色的瓷砖，并且你站在这块瓷砖上。该字符在每个数据集合中唯一出现一次。

当在一行中读入的是两个零时，表示输入结束。

输出格式
对每个数据集合，分别输出一行，显示你从初始位置出发能到达的瓷砖数(记数时包括初始位置的瓷砖)。

数据范围
$1 \leq W, H \leq 20$
输入样例：
6 9
…#. .
…#. .
… …
… …
… …
… …
… …
#@…#
.#…#.
0 0
输出样例：
45
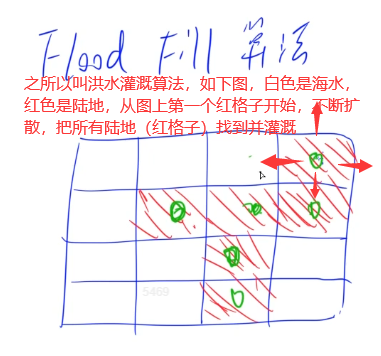
在这里插入图片描述

Flood Fill算法一般都可以用BFS和DFS实现。

BFS伪代码如下

while 队列非空{
	取出队列的头 t
	枚举t的四个邻格
		if(格子是陆地，且还未被灌溉){
		标记为已被灌溉
		插入到队列尾部
		}		
}

这道题有一个比较坑的地方就是第一个数表示的是列，第二个数才表示的是行
还有一个需要注意的地方就是因为这道题是连续的输入输出,即题中所说的包含多个数据集合，所以标记数组每次都需要初始化
思路：
首先先读入数据（注意第一个数表示列，第二个数才表示行），在读入的同时记录下站着的黑色瓷砖的位置
然后就是宽搜的模板
以这个站着的黑色瓷砖为中心，向四个方向进行扩散，如果扩散到的位置没有越界，并且是黑色瓷砖，并且之前没有遍历过，就把这个瓷砖加入到队列中（等待着之后以这个瓷砖为中心扩散）同时对这个瓷砖进行标记，表示这个瓷砖已经被遍历过。

import java.io.BufferedInputStream;
import java.util.LinkedList;
import java.util.Queue;
import java.util.Scanner;

public class Main {
    public static void main(String[] args) {
        Scanner scanner = new Scanner(new BufferedInputStream(System.in));
        while(scanner.hasNext()){ //由于有多组数据，所以用一个while循环（示例中只给了一组数据而已）
            int m = scanner.nextInt();//题目中是先输入的列，我们习惯用m代表列
            int n = scanner.nextInt();
            //输入的是两个0代表本组数据结束，应该去读取下一组数据了，即重新去进while循环
            if(m == 0 && n == 0) break;
            char[][] arr = new char[n][m];
            boolean[][] isVisited = new boolean[n][m];//标记数组，用于标记该格子是否访问过

            int x = 0 ,y = 0;
            for(int i = 0;i < n;i++){
                char[] chs = scanner.next().toCharArray();//chs的长度就是m
                for(int j = 0;j < m;j++){
                    arr[i][j] = chs[j];
                    if(arr[i][j] == '@'){//起点位置
                        x = i;
                        y = j;
                    }
                }
            }
            System.out.println(bfs(x,y,arr,isVisited));

        }
    }

    public static int bfs(int x,int y,char[][] arr,boolean[][] isVisited){
        Queue<Node> queue = new LinkedList<>();//Queue是接口，LinkedList是其一个实现类
        queue.add(new Node(x,y));//将第一个格子加入队列
        isVisited[x][y] = true;
        int res = 1;//起点本身也算一个可到达的格子，故res初始值是1
        int[] dx = {-1,0,1,0};//上右下左
        int[] dy = {0,1,0,-1};
        while(!queue.isEmpty()){
            Node node = queue.poll();
            for(int i = 0;i < 4;i++){
                int a = node.x + dx[i];//下一个要被访问的格子的坐标
                int b = node.y + dy[i];
                //下一个要访问的格子没有越界且没有被访问过才进行后续的操作
                if(a >= 0 && a < isVisited.length && b >= 0 && b < isVisited[0].length && !isVisited[a][b] ){
                    //如果是'.'表示可以访问，将该坐标加入队列尾，并标记该格子已访问，计数加1
                    if(arr[a][b] == '.'){
                        queue.add(new Node(a,b));
                        isVisited[a][b] = true;
                        res += 1;
                    }
                }
            }
        }
        return res;
    }
}

//代表坐标的类,用于宽搜时将坐标存入队列
class Node{
    public int x;
    public int y;
    Node(int x,int y){
        this.x = x;
        this.y = y;
    }
}

在这里插入图片描述

DFS

import java.io.BufferedInputStream;
import java.util.Scanner;

public class Main {
    public static void main(String[] args) {
        Scanner scanner = new Scanner(new BufferedInputStream(System.in));
        while(scanner.hasNext()){
            int m = scanner.nextInt();
            int n = scanner.nextInt();
            if(m == 0 && n == 0) break;
            char[][] arr = new char[n][m];
            boolean[][] isVisited = new boolean[n][m];

            int x = 0,y = 0;
            for(int i = 0 ;i < n ;i++){
                char[] chs = scanner.next().toCharArray();
                for(int j = 0;j < m;j++){
                    arr[i][j] = chs[j];
                    if(arr[i][j] == '@'){
                        x = i;
                        y = j;
                    }
                }
            }

            System.out.println(dfs(x,y,arr,isVisited));
        }
    }

    private static int dfs(int x, int y, char[][] arr, boolean[][] isVisited) {
        isVisited[x][y] =  true;
        int res = 1;
        int[] dx = {-1,0,1,0};//上右下左
        int[] dy = {0,1,0,-1};
        for(int i = 0;i < 4;i++){
            int a = x + dx[i];
            int b = y + dy[i];
            if(a >= 0 && a < arr.length && b >= 0 && b < arr[0].length && !isVisited[a][b]){
                if(arr[a][b] == '.'){
                    res += dfs(a,b,arr,isVisited);//让结果加上从a,b作为起点出发可以到达的所有格子数
                }
            }
        }
        return res;
    }
}