查找二叉树（BST）

50 阅读 0 评论 33 点赞

我是靠谱客的博主酷酷鸵鸟，最近开发中收集的这篇文章主要介绍查找二叉树（BST），觉得挺不错的，现在分享给大家，希望可以做个参考。

概述

今天分享一些关于BST的内容：
一、基础知识点
1 一棵树最上面的节点称为根节点，如果一个节点下面连接多个节点，那么该节点称为父节点，，，它下面的节点称为子节点。一个节点可以有0个 1个或多个子节点，没有任何子节点的节点称为叶子节点
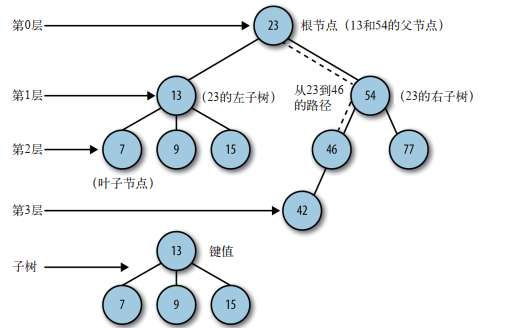
在这里插入图片描述
2 以某种特定的顺序访问树中所有的节点称为树的遍历

3 树可以分为几个层次，根节点是第0层，子节点是第1层，子节点的子节点是第2层，依次类推

二、今天的主角儿–BST
什么是BST?
BST（二叉查找树）：相对较小的值保存在左节点中，相对较大的值保存在右节点中，—查找效率高（这一特性）。
什么样的树才符合BST?
（1）若左子树不空，则左子树上所有结点的值均小于它的根结点的值；
（2）若右子树不空，则右子树上所有结点的值均大于它的根结点的值；
（3）左、右子树也分别为二叉排序树；
（4）没有键值相等的结点。

三、实现一棵查找二叉树
采用es6模块化
BST.js用于创建bst类以及一些方法（插入、前序、后序、中序遍历的方法）
BST.js如下：

import Node from "./Node.js";
export default class BST extends Node{
    root=null;
    constructor(){
        //继承超类
        super();
    }
    //用于输出数据

    //创建BST类，包括的方法有插入，前序，中序，后续遍历
    insert(data){
        var n = new Node(data,null,null);
        console.log(n)
        //判断根节点是否为空
        if(this.root===null){
            this.root=n;
        }else{
            var current=this.root;
            var parent;
            while(true){
                parent=current;
                //
                if(data<current.data){
                    current=current.left;
                    if(current===null){
                        parent.left=n;
                        break;
                    }
                }else{
                    current=current.right;
                    if(current===null){
                        parent.right=n;
                        break;
                    }
                }
            }
        }
    }
    //中序遍历
    inOrder(node){
        if(node!==null){
            //递归先遍历左子树
            this.inOrder1(node.left);
            //打印输出数据
            console.log("a"+node.show());
            //递归遍历右子树
            this.inOrder6(node.right);
        }
    }
    //先序遍历
    preOrder(node){
        if(node!==null){
            console.log(node.show());
            preOrder(node.left);
            preOrder(node.right);
        }
    }
    //后序遍历
    postOrder(node){
        if(node!==null){
            postOrder(node.left);
            postOrder(node.right);
            conosle.log(node.show());
        }
    }
}

Node.js主要用于创建节点

export default class Node{
//一个节点包含值，左右子节点
    constructor(data,left,right){
        this.data=data;
        this.left=left;
        this.right=right;
    }
   //show方法用来打印出节点的值
    show(){
        return this.data;
    }
}

调用：
html页面引入即可
测试效果

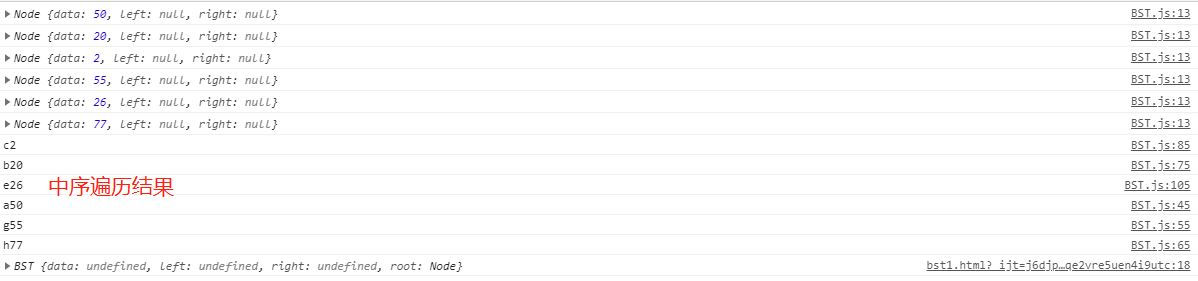
在这里插入图片描述
四、二叉查找树的删除、查找最大最小值、定值查找问题
1、获取最大值和最小值

//不停的遍历左子树，直到为null，返回最小值
 function getMin(){
        var current=this.root;
        while(!(current.left===null)){
            current=current.left;
        }
        return current.data;

    }

	//不停的遍历右子树，直到为null返回最大值
    function getMax(){
        var current=this.root;
        while(!(current.right===null)){
            current=current.right;
        }
        return current.data;
    }

2、删除某一个子节点
思路：让待删除的节点和根节点进行比较，分三种情况：大于（和右子节点继续比较），小于（就和左子节点继续比较）；等于（需要判断该节点有没有子节点，如果有一个没有就返回null；如果有一个节点，就返回该节点；如果有两个子节点，就查找待删除节点左子树上的最大值或者查找其右子树上的最小值。）

getSmallest(node) {
        if (node.left == null) {
            return node;
        }
        else {
            return getSmallest(node.left);
        }
    }
    removeNode(node,data){
        console.log("aaa");
        if(node===null){
            return null;
        }
        if(data===node.data){
            if(node.left===null && node.right===null){
                console.log("ddd");
                return null;
            }
            if(node.left===null){
                return node.right;
            }
            if(node.right===null){
                return node.left;
            }
			//这里采用的是查找右子树的最小值
            var tempNode=this.getSmallest(node.right);
            node.data=tempNode.data;
            node.right=removeNode(node.right,tempNode.data);
            return node;
        }else if(data<node.data){
            node.left=removeNode(node.left,data);
            return node;
        }else if(data>node.data){
            console.log("123456");
            node.right=removeNode(node.right,data);
            return node;
        }
    }
    var b = new BST();
    b.removeNode(b.root,25);

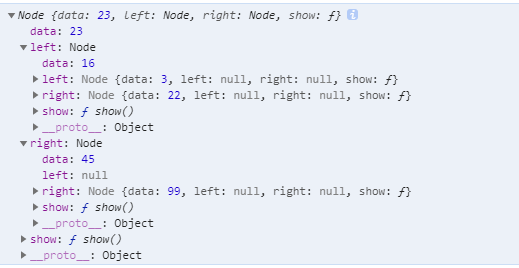
3、查找某个节点

		find(data){
        var current=this.root;
        while(!(current===null)){
            if(current.data===data){
                return current;
            }else if(current.data>data){
                current=current.left;
            }else{
                current=current.left;
            }
        }
        //空树就返回一个空
        return null;
    }