机器学习笔记19——集成/提升（Boosting）系列算法之AdaBoost 算法原理以及python实现引言1、概述2、基本思想3、算法4、算法实现5、小结

引言

quad quad 在集成学习介绍中，简单的介绍了Boosting方法的学习机制：先从初始训练集训练出一个基学习器，再根据基学习器的表现对训练样本分布进行调整，使得先前基学习器做错的的训练样本在后续受到更多关注，然后基于调整后的样本分布训练下一个基学习器；重复进行，直到基学习器数目达到事先指定的值T，最终将这T个基学习器加权结合。

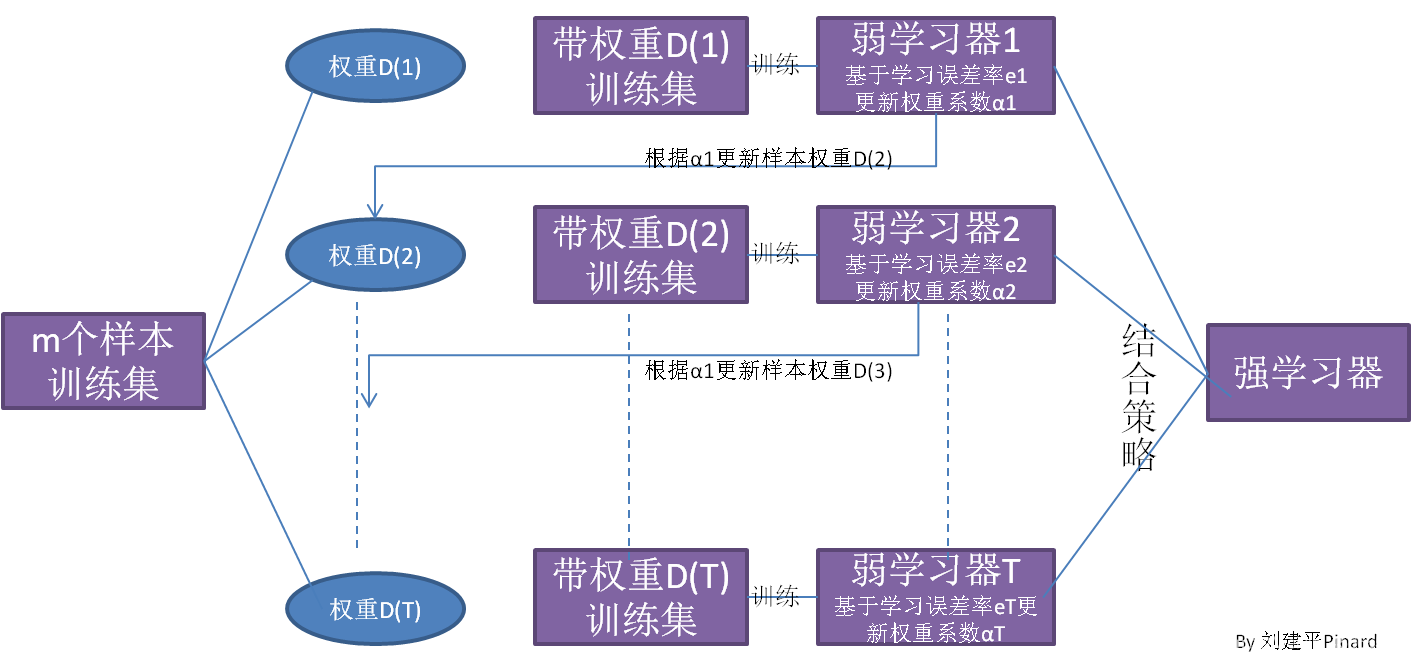
下面讲述Boosting方法之Adaboost 算法。

1、概述

quad quad AdaBoost（adapt boost），自适应推进算法，是一种通过改变训练样本权重来学习多个弱分类器并进行线性结合的过程，已被广泛应用人脸表情识别、图像检索等应用中。就目前而言，对Adaboost算法的研究以及应用大多集中于分类问题，在一些回归问题上也有所应用。Adaboost主要解决的问题有: 两类问题、多类单标签问题、多类多标签问题、回归问题。

2、基本思想

1）在训练过程中如何改变训练数据的权值或概率分布?

• 提高被弱分类器错分样本的权值，降低正分样本的权值，作为下一轮基本分类器的训练样本。这样一来，那些没有得到正确分类的数据，由于其价值加大后收到后一轮弱分类器的更大关注，于是，分类问题被一系列弱分类器"分而治之"。

2）如何将弱分类器组合成强分类器？

• 采取加权多数表决的方法，误差率小的分类器的权值大，使其在表决过程中起较大作用。

quad quad 具体过程：
quad quad 开始时，所有样本的权重相同，训练得到第一个基分类器。从第二轮开始，每轮开始前都先根据上一轮基分类器的分类效果调整每个样本的权重，上一轮分错的样本权重提高，分对的样本权重降低。之后根据新得到样本的权重指导本轮中的基分类器训练，即在考虑样本不同权重的情况下得到本轮错误率最低的基分类器。重复以上步骤直至训练到约定的轮数结束，每一轮训练得到一个基分类器。

3、算法

quad quad 使用最广泛的Adaboost弱学习器是决策树和神经网络。对于决策树，Adaboost分类用了CART分类树，而Adaboost回归用了CART回归树。

3.1 AdaBoost分类问题算法流程

quad quad AdaBoost利用以下算法，从训练数据中学习一系列弱分类器或基分类器，并将这些弱分类器线性组合成为一个强分类器。

算法8.1 Adaboost算法
输入：训练数据集 T = { ( x 1 , y 1 ) , ( x 2 , y 2 ) , … , ( x N , y N ) } T={left(x_1,y_1right),left(x_2,y_2right),dots,left(x_N,y_Nright)} T={(x1​,y1​),(x2​,y2​),…,(xN​,yN​)}；其中，$x_i\in \chi \subseteq R^n$ , y i ∈ γ = { − 1 , + 1 } y_iingamma={-1,+1} yi​∈γ={−1,+1} ；弱学习算法即弱学习器；
输出：最终分类器G(x)
（1）初始化训练数据的权值分布
$$D_1=(w_{11},...,w_{1i},...,w_{1N}),w_{1i}=\frac{1}{N},i=1,2,...,N$$
（2）对$m=1,2,\dots ,M$
（a）使用具有权值分布$D_m$的训练数据集学习，得到基分类器
G m ( x ) : χ → { − 1 , + 1 } G_m(x):chirightarrow{-1,+1} Gm​(x):χ→{−1,+1}
（b）计算$G_m(x)$在训练数据集上的分类误差率——Q(1)
$$e_m=P(G_m(x_i)\ne y_i)=\sum _{i=1}^N{w}_{mi}I(G_m(x_i)\ne y_i)\text{\hspace{1em}(8.1)}$$
（c）计算$G_m(x)$的系数——Q（2）
$${\alpha }_m=\frac{1}{2}log\frac{1-e_m}{e_m}\text{\hspace{1em}(8.2)}$$
这里的对数是自然对数,${\alpha }_m$表示$G_m(x)$在最终分类器中的重要性。【当$e_m\le \frac{1}{2}$时，${\alpha }_m\ge 0$,并且${\alpha }_m$随着$e_m$的减小而增大，所以分类误差率越小的基分类器在最终分类器中的作用越大。】
（d）更新训练数据集的权值分布——Q(3)
$$D_{m+1}=(w_{m+1,1},...,w_{m+1,i},...,w_{m+1,N})\text{\hspace{1em}(8.3)}$$$$w_{m+1,i}=\frac{w_{mi}}{Z_m}exp(-{\alpha }_m{y}_i{G}_m(x_i)),i=1,2,...,N\text{\hspace{1em}(8.4)}$$
这里，$Z_m$是规范化因子
$$Z_m=\sum _{i=1}^N{w}_{mi}exp(-{\alpha }_m{y}_i{G}_m(x_i))\text{\hspace{1em}(8.5)}$$
它使$D_m+1$成为一个概率分布
（3）构建基本分类器的线性组合
$$f\left(x\right)=\sum _{i=1}^m{\alpha }_m{G}_m(x)\text{\hspace{1em}(8.6)}$$
得到最终分类器——Q（4）$$G(x)=sign(f(x))=sign(\sum _{i=1}^m{\alpha }_m{G}_m(x))\text{\hspace{1em}(8.7)}$$

quad quad Adaboost一般使用单层决策树—decision stump【也称决策树桩，它是一种简单的决策树，通过给定的阈值，进行分类。】
作为其弱分类器。单层决策树是决策树的最简化版本，只有一个决策点，也就是说，如果训练数据有多维特征，单层决策树也只能选择其中一维特征来做决策，并且还有一个关键点，决策的阈值也需要考虑。
单层决策树生成函数

伪代码：

• 将最小错误率minError设为Inf(正无穷)
• 对于数据集每一个特征：（第一层循环）
  • 对于数据集每一个步长：（第二层循环）
    • 对每个不等号：（第三层循环）
      建立一颗决策树并用加权数据集对它进行测试
      如果错误率低于minError,将当前决策树设为最佳单层决策树
• 返回最佳单层决策树

3.2 Adaboost回归问题的算法流程

quad quad AdaBoost回归算法变种很多，下面主要讲解以下AdaBoost R2回归算法过程

输入：训练数据集 T = { ( x 1 , y 1 ) , ( x 2 , y 2 ) , … , ( x N , y N ) } T={left(x_1,y_1right),left(x_2,y_2right),dots,left(x_N,y_Nright)} T={(x1​,y1​),(x2​,y2​),…,(xN​,yN​)}；弱学习算法即弱学习器；弱学习器迭代次数K。
输出：最终分类器G(x)
（1）初始化训练数据的权值分布
$$D_1=(w_{11},...,w_{1i},...,w_{1N}),w_{1i}=\frac{1}{N},i=1,2,...,N$$
（2）对$m=1,2,\dots ,M$
（a）使用具有权值分布$D_m$的训练数据集学习，得到基分类器
$G_m(x)$
（b）计算$G_m(x)$在训练数据集上的最大误差
$$E_m=max|y_i-G_m(x_i)|,i=1,2,...,N$$
（c）计算每个样本的相对误差：

• 如果是线性误差，则$e_{mi}=\frac{|y_i-G_m(x_i)|}{E_m}$
• 如果是平方误差，则$e_{mi}=\frac{(y_i-G_m(x_i){)}^2}{E_m^2}$
• 如果是指数误差，则$e_{mi}=1-exp(\frac{-|y_i-G_m(x_i)|}{E_m})$

（d）计算回归误差率
$$e_m=\sum _{i=1}^N{w}_{mi}{e}_{mi}$$

（e）计算弱学习器的系数
$${\alpha }_m=\frac{e_m}{1-e_m}$$
（f）更新样本集的权重分布
$$w_{m+1,i}=\frac{w_{mi}}{Z_m}{\alpha }_m^{1-e_{mi}}$$
其中，$Z_m$为规范化因子，$$Z_m=\sum _{i=1}^N{w}_{mi}{\alpha }_m^{1-e_{mi}}$$
（3）构建最终学习器为：
$$f(x)=G_{m^{\ast }}(x)$$
其中，$G_{m^{\ast }}(x)$是所有$ln\frac{1}{{\alpha }_m},m=1,2,...,M$的中位数值对应序号$m^{\ast }$对应的弱学习器。

3.3 AdaBoost算法的正则化

quad quad 为了防止AdabBoost过拟合，我们通常也会加入正则化项，这个正则化项我们通常称为步长(learning rate)。定义为$\nu$,对于前面的弱学习器的迭代
$$f_m(x)=f_{m-1}(x)+{\alpha }_m{G}_m(x)$$
如果我们加上了正则化项，则有
$$f_m(x)=f_{m-1}(x)+v{\alpha }_m{G}_m(x)$$
其中，$\nu$的取值范围为$0<\nu \le 1$。对于同样的训练集学习效果，较小的$\nu$意味着我们需要更多的弱学习器的迭代次数。通常我们用步长和迭代最大次数一起来决定算法的拟合效果。

4、算法实现

4.1 手写实现Adaboost分类问题

在每一次构造训练器时：

• 在指定权重分布D下训练出最佳的单层决策树
• 将最佳的单层决策树加入单层决策树集合
• 计算alpha
• 更新权重分布D
• 如果分类错误率为0，则退出循环
  返回单层决策树集合

1、导入库

import numpy as np
import pandas as pd
from sklearn.datasets import load_iris
from sklearn.model_selection  import train_test_split
import matplotlib.pyplot as plt
%matplotlib inline

2.导入鸢尾花数据集并创建数据集以及类别标签

def create_data():
    iris = load_iris()
    df = pd.DataFrame(iris.data, columns=iris.feature_names)
    df['label'] = iris.target
    df.columns = ['sepal length', 'sepal width', 'petal length', 'petal width', 'label']
    data = np.array(df.iloc[:100, [0, 1, -1]])
    for i in range(len(data)):
        if data[i,-1] == 0:
            data[i,-1] = -1
    # print(data)
    return data[:,:2], data[:,-1]
# 执行算法
X, y = create_data()
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.33)

3、构建Adaboost

class AdaBoost:
    def __init__(self, n_estimators=50, learning_rate=1.0):
        self.clf_num = n_estimators   # 分类器的个数
        self.learning_rate = learning_rate   # 移动步伐
    def init_args(self, datasets, labels):
        self.X = datasets  # 样本数据
        self.Y = labels  # 样本分类类别
        self.M, self.N = datasets.shape   # 样本的个数和特征数
        self.clf_sets = []  # 弱分类器数目和集合
        self.weights = [1.0 / self.M] * self.M    # 初始化weights，1/m，共有m个。
        self.alpha = []  # G(x)系数 alpha
    #基于单层决策树构建弱分类器
    # 选的哪个特征后，找出最佳特征值
    def _G(self, features, labels, weights):
        m = len(features)
        error =100000#错误率最大化
        best_v = 0.0
        # 单维features
        #考到数值型的特征，我们就可以通过计算最小值和最大值来 解应该需要多大的步长
        features_min = min(features)
        features_max = max(features)
        n_step = (features_max - features_min +
                  self.learning_rate) // self.learning_rate
        direct, compare_array = None, None
        for i in range(1, int(n_step)):#补偿范围
            v = features_min + self.learning_rate * i
            if v not in features:#误分类计算
                compare_array_positive = np.array(
                    [1 if features[k] > v else -1 for k in range(m)])
                weight_error_positive = sum([
                    weights[k] for k in range(m)
                    if compare_array_positive[k] != labels[k]
                ])

                compare_array_nagetive = np.array(
                    [-1 if features[k] > v else 1 for k in range(m)])
                weight_error_nagetive = sum([
                    weights[k] for k in range(m)
                    if compare_array_nagetive[k] != labels[k]
                ])

                if weight_error_positive < weight_error_nagetive:
                    weight_error = weight_error_positive
                    _compare_array = compare_array_positive
                    direct = 'positive'
                else:
                    weight_error = weight_error_nagetive
                    _compare_array = compare_array_nagetive
                    direct = 'nagetive'
                # print('v:{} error:{}'.format(v, weight_error))
                if weight_error < error:
                    error = weight_error
                    compare_array = _compare_array
                    best_v = v
        return best_v, direct, error, compare_array

    # 计算alpha
    def _alpha(self, error):
        return 0.5 * np.log((1 - error) / error)

    # 规范化因子
    def _Z(self, weights, a, clf):
        return sum([
            weights[i] * np.exp(-1 * a * self.Y[i] * clf[i])
            for i in range(self.M)
        ])
    # 权值更新
    def _w(self, a, clf, Z):
        for i in range(self.M):
            self.weights[i] = self.weights[i] * np.exp(
                -1 * a * self.Y[i] * clf[i]) / Z

    # G(x)的线性组合
    def _f(self, alpha, clf_sets):
        pass
    def G(self, x, v, direct):
        if direct == 'positive':
            return 1 if x > v else -1
        else:
            return -1 if x > v else 1
    def fit(self, X, y):
        self.init_args(X, y)
        for epoch in range(self.clf_num):
            best_clf_error, best_v, clf_result = 100000, None, None
            # 在众多特征中，选出误差最小的特征
            for j in range(self.N):
                features = self.X[:, j]
                # 分类阈值，分类误差，分类结果
                v, direct, error, compare_array = self._G(features, self.Y, self.weights)
                if error < best_clf_error:
                    best_clf_error = error      # 分类误差
                    best_v = v                  # 分类特征值
                    final_direct = direct       # 判断是大于特征值为1 还是小于特征值为1
                    clf_result = compare_array  # 分类结果
                    axis = j                    # 特征索引
                if best_clf_error == 0:         # 如果误差为0，就直接选择该特征和特征值
                    break
            # 计算G(x)系数a
            a = self._alpha(best_clf_error)
            self.alpha.append(a)
            # 记录分类器
            self.clf_sets.append((axis, best_v, final_direct))
            Z = self._Z(self.weights, a, clf_result)
            # 权值更新
            self._w(a, clf_result, Z)
            
    # 模型预测，进行分类分类
    def predict(self, feature):
        result = 0.0
        for i in range(len(self.clf_sets)):
            axis, clf_v, direct = self.clf_sets[i]
            f_input = feature[axis]
            result += self.alpha[i] * self.G(f_input, clf_v, direct)
        return 1 if result > 0 else -1
    #模型准确率
    def score(self, X_test, y_test):
        right_count = 0
        for i in range(len(X_test)):
            feature = X_test[i]
            if self.predict(feature) == y_test[i]:
                right_count += 1
        return right_count / len(X_test)

4、训练模型

clf = AdaBoost(n_estimators=10, learning_rate=0.2)
clf.fit(X_train, y_train)
clf.score(X_test, y_test)

4.2 基于sklearn实现Adaboost算法（python）

Scikit-Learn AdaBoost官方文档

4.2.1 AdaBoost类库概述

quad quad Scikit-Learn中Adaboost类库比较直接就是AdaBoostClassifier和AdaBoostRegressor两个，从名字就可以看出AdaBoostClassifier用于分类，AdaBoostRegressor用于回归。

quad quad AdaBoostClassifier使用了两种Adaboost分类算法的实现，SAMME和SAMME.R。而AdaBoostRegressor则使用了我们原理篇里讲到的Adaboost回归算法的实现，即Adaboost.R2。

quad quad 当我们对Adaboost调参时，主要是对两部分内容进行调参，第一部分是对我们的Adaboost的框架进行调参， 第二部分是对我们选择的弱分类器进行调参。两者相辅相成。下面就对Adaboost的两个类：AdaBoostClassifier和AdaBoostRegressor从这两部分做一个介绍。

4.2.2 sklearn.ensemble.AdaBoostClassifier简介以及实战

官方文档

sklearn.ensemble.AdaBoostClassifier()函数全称AdaBoost分类器。

class sklearn.ensemble.AdaBoostClassifier(base_estimator=None, n_estimators=50, 
										learning_rate=1.0, algorithm=’SAMME.R’, 
										random_state=None)

参数：

• base_estimator： 可选参数，默认为无。

  理论上可以选择任何一个分类或者回归学习器，不过需要支持样本权重。我们常用的一般是CART决策树或者神经网络MLP。默认是决策树，即AdaBoostClassifier默认使用CART分类树DecisionTreeClassifier，而AdaBoostRegressor默认使用CART回归树DecisionTreeRegressor。另外有一个要注意的点是，如果我们选择的AdaBoostClassifier算法是SAMME.R，则我们的弱分类学习器还需要支持概率预测，也就是在scikit-learn中弱分类学习器对应的预测方法除了predict还需要有predict_proba。

• n_estimators： 整数型，可选参数，默认为50。

  弱学习器的最大迭代次数，或者说最大的弱学习器的个数。一般来说n_estimators太小，容易欠拟合，n_estimators太大，又容易过拟合，一般选择一个适中的数值。默认是50。在实际调参的过程中，我们常常将n_estimators和下面介绍的参数learning_rate一起考虑。

• learning_rate： 浮点型，可选参数，默认为1.0。

  每个弱学习器的权重缩减系数，取值范围为0到1，对于同样的训练集拟合效果，较小的v意味着我们需要更多的弱学习器的迭代次数。通常我们用步长和迭代最大次数一起来决定算法的拟合效果。所以这两个参数n_estimators和learning_rate要一起调参。一般来说，可以从一个小一点的v开始调参，默认是1。

• algorithm： 可选参数，默认为SAMME.R。

  scikit-learn实现了两种Adaboost分类算法，SAMME和SAMME.R。两者的主要区别是弱学习器权重的度量，SAMME使用对样本集分类效果作为弱学习器权重，而SAMME.R使用了对样本集分类的预测概率大小来作为弱学习器权重。由于SAMME.R使用了概率度量的连续值，迭代一般比SAMME快，因此AdaBoostClassifier的默认算法algorithm的值也是SAMME.R。我们一般使用默认的SAMME.R就够了，但是要注意的是使用了SAMME.R， 则弱分类学习器参数base_estimator必须限制使用支持概率预测的分类器。SAMME算法则没有这个限制。

• random_state： 整数型，可选参数，默认为None。

  如果RandomState的实例，random_state是随机数生成器; 如果None，则随机数生成器是由np.random使用的RandomState实例。

方法：

实战：

quad quad 同样利用上述数据集进行分类，只不过调用sklearn库中三种分类器进行一 一对比。

from sklearn.model_selection import train_test_split
from sklearn.ensemble import AdaBoostClassifier
from sklearn.tree import DecisionTreeClassifier
from sklearn.neighbors import KNeighborsClassifier


# 创建数据集
def create_data():
    iris = load_iris()
    df = pd.DataFrame(iris.data, columns=iris.feature_names)
    df['label'] = iris.target
    df.columns = ['sepal length', 'sepal width', 'petal length', 'petal width', 'label']
    data = np.array(df.iloc[:100, [0, 1, -1]])
    for i in range(len(data)):
        if data[i,-1] == 0:
            data[i,-1] = -1
    # print(data)
    return data[:,:2], data[:,-1]
# 加载数据集
X, y = create_data()
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.33)
# 1、AdaBoost 分类器
ada=AdaBoostClassifier( )
ada.fit(X_train,y_train)
print('AdaBoost 精确率=',ada.score(X_test,y_test))

# 2、决策树分类器
dt=DecisionTreeClassifier()
dt.fit(X_train,y_train)
dt.score(X_test,y_test)
print('决策树 精确率=',ada.score(X_test,y_test))

# 3、KNN分类器
knn=KNeighborsClassifier()
knn.fit(X_train,y_train)
knn.score(X_test,y_test)
print('KNN 精确率=',knn.score(X_test,y_test))

输出结果：

AdaBoost 精确率= 0.8484848484848485
决策树 精确率= 0.8484848484848485
knn决策树 精确率= 1.0

4.2.3 sklearn.ensemble.AdaBoostRegressor简介以及实战

官方文档

class 
sklearn.ensemble.AdaBoostRegressor(base_estimator=None, *, n_estimators=50, 
learning_rate=1.0, loss='linear', random_state=None)

下面使用SKlearn库中的波士顿房价数据集进行以下两个实战。用AdaBoost对房价进行预测: 首先加载数据，将数据分割成训练集和测试集，然后创建 AdaBoost 回归模型， 传入训练集数据进行拟合，再传入测试集数据进行预测，就可以得到预测结果。 最后将预测的结果与实际结果进行对比，得到两者之间的误差。

实战一：

目的：构建AdaBoostRegressor模型预测房价并探究使用哪种损失函数比较好

from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_squared_error
from sklearn.datasets import load_boston
from sklearn.ensemble import AdaBoostRegressor 
# 加载数据
data=load_boston()
# 分割训练集与测试集
train_x,test_x,train_y,test_y=train_test_split(data.data,data.target,test_size=0.25,random_state=33)

# 1、使用AdaBoostRegressor 模型，默认情况下损失函数为linear
regressor=AdaBoostRegressor( )
regressor.fit(train_x,train_y)
pred_y = regressor.predict(test_x)
mse_AdaBoostRegressor_linear = mean_squared_error(test_y, pred_y)
#print("房价预测结果 ", pred_y)
print("AdaBoostRegressor_linear均方误差 = ",round(mse_AdaBoostRegressor_linear,2))

# 2、损失函数改为平方形式
regressor=AdaBoostRegressor(base_estimator=None,n_estimators=50,learning_rate=1.0,loss='square',random_state=1)
regressor.fit(train_x,train_y)
pred_y = regressor.predict(test_x)
mse_AdaBoostRegressor_square = mean_squared_error(test_y, pred_y)
#print("房价预测结果 ", pred_y)
print("AdaBoostRegressor_square均方误差 = ",round(mse_AdaBoostRegressor_square,2))

# 3、损失函数改为指数函数形式
regressor=AdaBoostRegressor(base_estimator=None,n_estimators=50,learning_rate=1.0,loss='exponential',random_state=1)
regressor.fit(train_x,train_y)
pred_y = regressor.predict(test_x)
mse_AdaBoostRegressor_exponential = mean_squared_error(test_y, pred_y)
#print("房价预测结果 ", pred_y)
print("AdaBoostRegressor_exponential均方误差 = ",round(mse_AdaBoostRegressor_exponential,2))

输出结果为：

AdaBoostRegressor_linear均方误差 =  17.65
AdaBoostRegressor_square均方误差 =  19.69
AdaBoostRegressor_exponential均方误差 =  16.79

可以看出，损失函数的对比中，对该数据来讲，指数损失函数预测效果最好。
对比中需要注意，随机数种子函数的类型需要设置相同，否则每次对比结果不同，对比的意义也就不存在了，损失函数对比中统一设置random_state=1。

实战二：

目的：AdaBoost回归、决策树回归、KNN回归房价预测对比

from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_squared_error
from sklearn.datasets import load_boston
from sklearn.ensemble import AdaBoostRegressor 
from sklearn.tree import DecisionTreeRegressor
from sklearn.neighbors import KNeighborsRegressor
# 加载数据
data=load_boston()
# 分割训练集与测试集
train_x,test_x,train_y,test_y=train_test_split(data.data,data.target,test_size=0.25,random_state=33)
# 1、使用AdaBoostRegressor 模型
regressor=AdaBoostRegressor(base_estimator=None,n_estimators=50,learning_rate=1.0,loss='exponential',random_state=1)
regressor.fit(train_x,train_y)
pred_y=regressor.predict(test_x)
mse=mean_squared_error(test_y,pred_y)
#print("房价预测结果：",pred_y)
'''
round(number,num_digits)

Number 需要进行四舍五入的数字。
Num_digits 指定的位数，按此位数进行四舍五入,即保留几位小数。
'''
print("AdaBoost均方误差=",round(mse,2))
# 2、使用决策树回归模型
dec_regressor=DecisionTreeRegressor()
dec_regressor.fit(train_x,train_y)
pred_y = dec_regressor.predict(test_x)
mse_DecisionTree = mean_squared_error(test_y, pred_y)
print("决策树均方误差 = ",round(mse_DecisionTree,2))
# 3、使用KNN回归模型
knn_regressor=KNeighborsRegressor()
knn_regressor.fit(train_x,train_y)
pred_y = knn_regressor.predict(test_x)
mse_knn = mean_squared_error(test_y, pred_y)
print("KNN均方误差 = ",round(mse_knn,2))
#print(regressor.feature_importances_)

# 4、特征得分可视化图

def plot_feature_importances(feature_importances,title,feature_names):
    #将重要性值标准化
    feature_importances=100.0*(feature_importances/max(feature_importances))
    #将得分从低到高进行排序flipub实现矩阵的翻转
    index_sorted=np.flipud(np.argsort(feature_importances))
    #让x坐标轴上的把标签居中shape用于读取矩阵的长度
    pos=np.arange(index_sorted.shape[0])+0.5
    #画出条形图
    plt.figure()
    #bar代表柱形图
    plt.bar(pos,feature_importances[index_sorted],align='center')
    #为x轴的主刻度设置值
    plt.xticks(pos,feature_names[index_sorted])
    plt.ylabel('Relative importances')
    plt.title(title)
    plt.show()
 
#特征重要性 图形表示feature_importances代表每个特征多样性
plot_feature_importances(regressor.feature_importances_,'Adaboost Regressor',housing_data.feature_names)
plot_feature_importances(dec_regressor.feature_importances_,'Decision Tree Regressor',housing_data.feature_names)

输出结果：

AdaBoost均方误差= 16.79
决策树均方误差 =  36.81
KNN均方误差 =  27.87

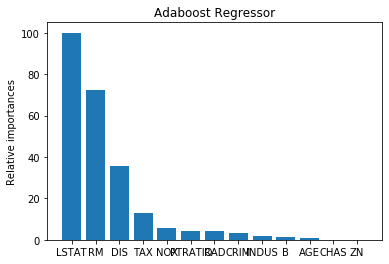
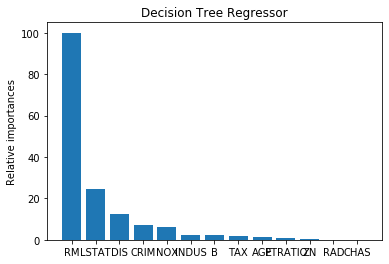
可以看出：AdaBoost模型较好。

5、小结

Adaboost的主要优点有：

1）Adaboost作为分类器时，分类精度很高

2）在Adaboost的框架下，可以使用各种回归分类模型来构建弱学习器，非常灵活。

3）作为简单的二元分类器时，构造简单，结果可理解。

4）不容易发生过拟合

Adaboost的主要缺点有：

对异常样本敏感，异常样本在迭代中可能会获得较高的权重，影响最终的强学习器的预测准确性。

参考资料：
1、李航《统计学习方法》
2、机器学习实战
3、https://blog.csdn.net/changzoe/article/details/78921624
4、https://github.com/ljpzzz/machinelearning/tree/master/ensemble-learning

最后

以上就是冷酷人生为你收集整理的机器学习笔记19——集成/提升（Boosting）系列算法之AdaBoost 算法原理以及python实现引言1、概述2、基本思想3、算法4、算法实现5、小结的全部内容，希望文章能够帮你解决机器学习笔记19——集成/提升（Boosting）系列算法之AdaBoost 算法原理以及python实现引言1、概述2、基本思想3、算法4、算法实现5、小结所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。