1. 首页
  2. 文章中心
  3. PyTorch

【PyTorch】RNN/LSTM/GRU 计算过程、参数以及使用RNN.LSTM.GRU.参考资料.

63 阅读 0 评论
我是靠谱客的博主 懦弱月光，最近开发中收集的这篇文章主要介绍【PyTorch】RNN/LSTM/GRU 计算过程、参数以及使用RNN.LSTM.GRU.参考资料.，觉得挺不错的，现在分享给大家，希望可以做个参考。

概述

文章目录

  • RNN.
    • 基本结构.
    • PyTorch - RNN.
      • 计算规则.
      • 构造参数.
      • 输入参数.
      • 输出参数.
      • 权重初始化.
      • 代码示例.
  • LSTM.
    • 基本结构.
    • PyTorch - LSTM.
      • 构造参数.
      • 输入参数.
      • 输出参数.
      • 代码示例.
  • GRU.
  • 参考资料.

RNN.

基本结构.

  • R N N rm RNN RNN 图示一般如下所示，有回边来体现循环这一特征。
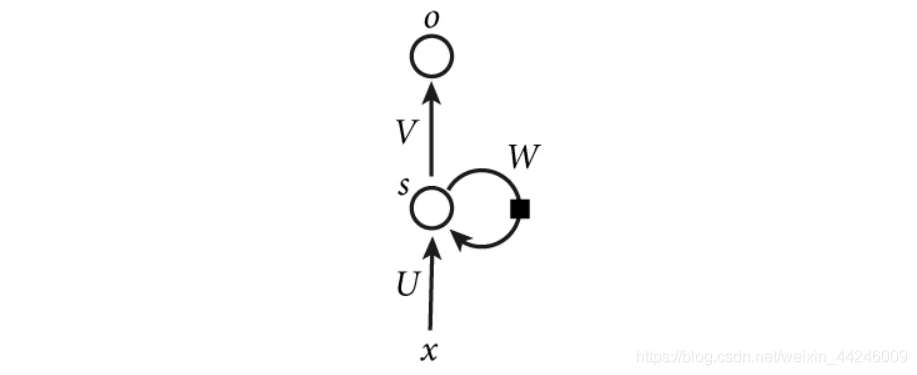
    在这里插入图片描述
    更容易直观理解的展开形式如下：
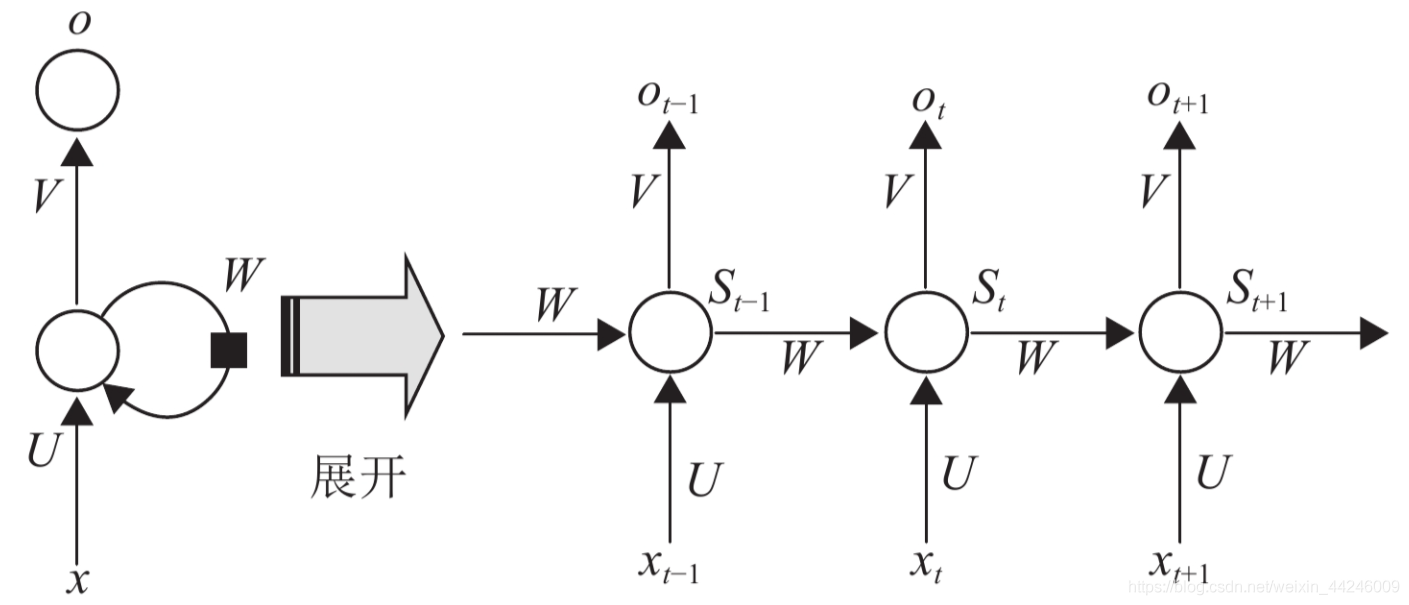    在这里插入图片描述网络中传播规则如下： o t = g ( V ⋅ S t ) (1) o_t=g(Vcdot S_t)tag{1} ot​=g(V⋅St​)(1) S t = f ( U ⋅ x t + W ⋅ S t − 1 ) (2) S_t=f(Ucdot x_t+Wcdot S_{t-1})tag{2} St​=f(U⋅xt​+W⋅St−1​)(2)其中 f , g f,g f,g 是激活函数，可以相同也可以不同，常用的有 R e L U , tanh ⁡ rm ReLU,tanh ReLU,tanh 等。
  • 【注意】我们将上述图示中 o t o_t ot​ 记为输出值， S t S_t St​ 记为隐层值。 P y T o r c h rm PyTorch PyTorch 中并没有严格的按照上图以及 ( 1 ) , ( 2 ) (1),(2) (1),(2) 两式构造循环神经网络，其中的区别在下面介绍。

PyTorch - RNN.

  • 上面介绍的是基本 R N N rm RNN RNN 单元，它是循环神经网络的最大特质体现， P y T o r c h rm PyTorch PyTorch 文档中定义基本 R N N rm RNN RNN 如下，逐步来剖析。
Applies a multi-layer Elman RNN with tanh or ReLU non-linearity to an input 
sequence.
  • 网络结构采用 E l m a n   R N N rm Elman~RNN Elman RNN，是 J e f f   E l m a n rm Jeff~Elman Jeff Elman 在 1990 1990 1990 年提出来的，于 J o r d a n   R N N   ( 1986 ) rm Jordan~RNN~(1986) Jordan RNN (1986) 的基础上进行了简化。 E l m a n   R N N rm Elman~RNN Elman RNN 的隐层输出经过时延后作为下一时刻隐层输入的一部分，然后隐层输出同时送到网络后续的层，比如最终的输出层。 J o r d a n   R N N rm Jordan~RNN Jordan RNN 则直接把整个网络最终输出层的输出经过时延后反馈回网络的输入层。
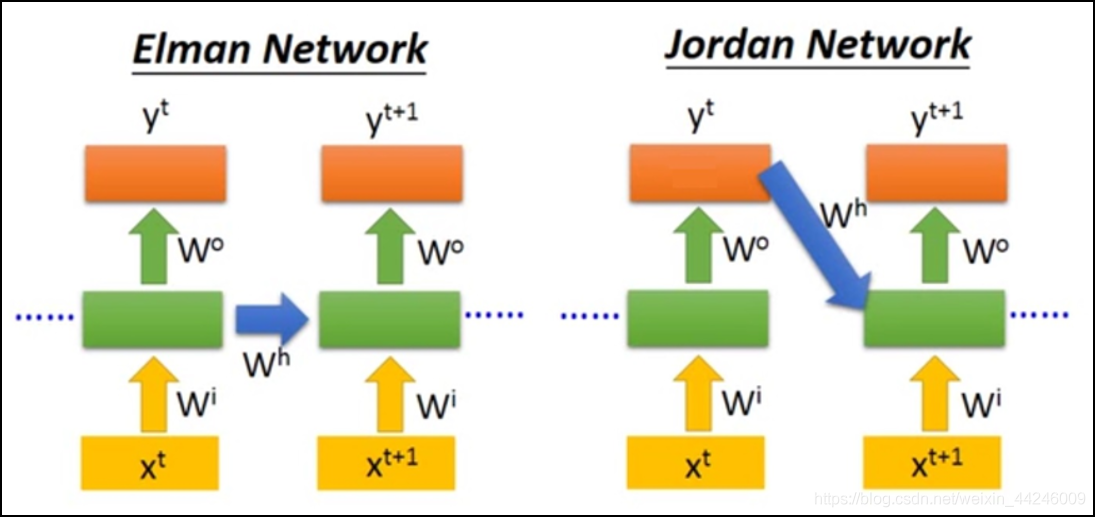
    在这里插入图片描述
    这里两种网络结构仅仅是理论上的结构，实际 P y T o r c h rm PyTorch PyTorch 中实现 E l m a n   R N N rm Elman~RNN Elman RNN 并未立即将隐层输出传递到输出层。

计算规则.

  • P y T o r c h − R N N rm PyTorch-RNN PyTorch−RNN 的传递规则如下，对于输入序列中的每个元素，网络隐层(可以有多个) 按照如下规则计算： h t = tanh ⁡ ( W i h x t + b i h + W h h h t − 1 + b h h ) (3) h_t=tanhBig(W_{ih}x_t+b_{ih}+W_{hh}h_{t-1}+b_{hh}Big)tag{3} ht​=tanh(Wih​xt​+bih​+Whh​ht−1​+bhh​)(3)其中 h t h_t ht​ 是第 t t t 位置时的隐层状态，也可以理解为隐层输出； x t x_t xt​ 是第 t t t 位置的输入； W i h , W h h W_{ih},W_{hh} Wih​,Whh​ 分别是从输入变量到隐层变量、隐层变量到隐层变量的权重矩阵，这一点观察下标很容易理解。将 ( 3 ) (3) (3) 和 ( 2 ) (2) (2) 做对比，不难发现其中： h t ↔ S t   ,   U ↔ W i h   ,   W ↔ W h h h_tleftrightarrow S_t~,~Uleftrightarrow W_{ih}~,~Wleftrightarrow W_{hh} ht​↔St​ , U↔Wih​ , W↔Whh​并且存在偏置项 b i h , b h h . b_{ih},b_{hh}. bih​,bhh​.
  • 另外需要注意的是，在整个序列被计算完之前， W i h , W h h , b i h , b h h W_{ih},W_{hh},b_{ih},b_{hh} Wih​,Whh​,bih​,bhh​ 是不会变化的，不同时刻的计算共享参数，直至输出后计算损失函数，后续执行反向传播过程。

构造参数.

  • P y T o r c h − R N N rm PyTorch-RNN PyTorch−RNN 构造时参数列举如下：
    在这里插入图片描述
  • i n u p u t _ s i z e rm inuput_size inuput_size 的释义略显模糊，具体地说，它是输入数据的特征数量。 P y T o r c h − R N N rm PyTorch-RNN PyTorch−RNN 接收形如 [ L , N , H i n ] [L,N,H_{in}] [L,N,Hin​] 的数据张量，其中 L L L 是序列长度 s e q u e n c e _ l e n g t h rm sequence_length sequence_length， N N N 是批大小， H i n H_{in} Hin​ 就是这里的 i n p u t _ s i z e . rm input_size. input_size. 举例自然语言处理中，如果我们需要分析一个句子，句子有 200 200 200 个单词，句子的每个单词都已经转化为 300 300 300 维词向量，那么该数据张量的维度就是 [ 200 , 1 , 300 ] . [200,1,300]. [200,1,300].
  • h i d d e n _ s i z e rm hidden_size hidden_size 是 R N N rm RNN RNN 中隐层的节点数目，此时已经接收到了维度是 300 300 300 的词向量，类比普通神经网络，即为输入维度是 300. 300. 300. 如果给定 h i d d e n _ s i z e = 100 rm hidden_size=100 hidden_size=100，那么隐层变量的维度就是 100. 100. 100. 此时回到 ( 3 ) (3) (3) 表示的单步计算，可以认为： h t , b i h , b h h ∈ R 100 h_t,b_{ih},b_{hh}inmathbb R^{100} ht​,bih​,bhh​∈R100 x t ∈ R 300 x_tinmathbb R^{300} xt​∈R300 W i h ∈ R 100 × 300   ;   W h h ∈ R 100 × 100 W_{ih}inmathbb R^{100times300}~;~W_{hh}inmathbb R^{100times100} Wih​∈R100×300 ; Whh​∈R100×100 b i h , b h h ∈ R 100 b_{ih},b_{hh}inmathbb R^{100} bih​,bhh​∈R100
  • n u m _ l a y e r s rm num_layers num_layers 是最容易产生误解的参数，看了上面 R N N rm RNN RNN 的展开图后，可能会将其理解为网络展开后的长度。但细细思考后不难发现，网络一轮计算何时停止，是由输入数据的序列长度决定的，例如这里我们假设句子长度为 200 200 200，那么网络展开后 t ∈ [ 0 , 200 ] . tin[0,200]. t∈[0,200]. 实际 n u m _ l a y e r s rm num_layers num_layers 是 P y T o r c h rm PyTorch PyTorch 中隐层层数，类比普通神经网络就不难理解了，只不过此处隐层的计算规则与彼时不同。以 n u m _ l a y e r s = 2 rm num_layers=2 num_layers=2 为例， P y t o c h − R N N rm Pytoch-RNN Pytoch−RNN 会将第一层计算得出的隐层值 h t 1 h_t^1 ht1​ 继续传递给第二隐层，因此计算规则可以简单地扩充如下： h t 1 = tanh ⁡ ( W i h 1 x t + b i h 1 + W h h 1 h t − 1 1 + b h h 1 ) (4.1) h_t^1=tanhBig(W_{ih}^1x_t+b_{ih}^1+W_{hh}^1h_{t-1}^1+b_{hh}^1Big)tag{4.1} ht1​=tanh(Wih1​xt​+bih1​+Whh1​ht−11​+bhh1​)(4.1) h t 2 = tanh ⁡ ( W i h 2 h t 1 + b i h 2 + W h h 2 h t − 1 2 + b h h 2 ) (4.2) h_t^2=tanhBig(W_{ih}^2h_t^1+b_{ih}^2+W_{hh}^2h_{t-1}^2+b_{hh}^2Big)tag{4.2} ht2​=tanh(Wih2​ht1​+bih2​+Whh2​ht−12​+bhh2​)(4.2)注意 h i d d e n _ s i z e rm hidden_size hidden_size 未改变，因此本例中 h t 2 ∈ R 100 . h_t^2inmathbb R^{100}. ht2​∈R100.
  • 其余参数的意义均比较明确，值得一提的是 b i d i r e c t i o n a l rm bidirectional bidirectional，它将决定网络是基本 R N N RNN RNN 还是能力更加强大的 B R N N rm BRNN BRNN，即双向循环神经网络。直观地说， R N N rm RNN RNN 在计算 h t h_t ht​ 时，只能将 i ∈ [ 0 , t − 1 ] iin[0,t-1] i∈[0,t−1] 位置的信息纳入考虑；但 B R N N rm BRNN BRNN 能够将 i ∈ [ 0 , L ] iin[0,L] i∈[0,L] 内的信息都纳入考虑，代价是更多的参数以及更大的计算量。

输入参数.

  • 使用 R N N rm RNN RNN 层进行前传时，需要给定输入数据和初始隐层状态 h 0 h_0 h0​，其中 h 0 h_0 h0​ 是可选的，如果不指定则默认使用全零向量。这里我们记输入数据组织为 [ L , N , H i n ] [L,N,H_{in}] [L,N,Hin​] 的维度形式，并且网络为基本循环神经网络，隐层数量为 N l N_l Nl​，隐层节点数为 H o u t H_{out} Hout​，那么初始隐层状态的维度是 [ N l , N , H o u t ] . [N_l,N,H_{out}]. [Nl​,N,Hout​].

输出参数.

  • P y T o r c h − R N N rm PyTorch-RNN PyTorch−RNN 中的输出并非严格按照 ( 1 ) (1) (1) 中直接计算 o t = g ( V ⋅ S t ) o_t=g(Vcdot S_t) ot​=g(V⋅St​)，而是将所有时刻 t t t 对应的最后隐层值组织成 [ L , N , H o u t ] [L,N,H_{out}] [L,N,Hout​] 形式的张量 o u t p u t rm output output 交给程序员，保证后续灵活的处理。
  • 其返回值分为两部分，第一部分就是 o u t p u t rm output output，第二部分则是 h _ n h_n h_n，它给出最后一个位置的所有隐层状态，其维度是 [ N l , N , H o u t ] . [N_l,N,H_{out}]. [Nl​,N,Hout​].
  • 总结来说， o u t p u t rm output output 给出所有位置在最后一个隐层的状态； h _ n h_n h_n 给出最后一个位置所有隐层状态。

权重初始化.

  • 关于 P y T o r c h − R N N rm PyTorch-RNN PyTorch−RNN 中参数的初始化，所有权重参数、偏置参数均从如下分布中随机产生： θ ∼ U n i ( − k , k )    ,    k = 1 h i d d e n _ s i z e (5) thetasim{rm Uni}(-sqrt k,sqrt k)~~,~~k=cfrac{1}{rm hidden_size}tag{5} θ∼Uni(−k ​,k ​)  ,  k=hidden_size1​(5)

代码示例.

  • 关于基本 R N N rm RNN RNN 的使用，代码示例如下所示，观察输入数据维度，初始隐层状态维度以及输出数据维度，与上述计算过程相互验证。
# In[Import]
import torch
import torch.nn as nn

# In[RNN]
H_in = 10
H_out = hidden_size = 20
N_l = 2
Rnn = nn.RNN(H_in,hidden_size,N_l)

# In[Data]
L = 50
N = 16
x = torch.randn(L,N,H_in)
h_0 = torch.randn(N_l,N,H_out)

# In[Cal]
output,h_n = Rnn(x)

# print('output:',output)
print('output size:',output.size())
# print('h_n:',h_n)
print('h_n size:',h_n.size())

'''
output size: torch.Size([50, 16, 20])
h_n size: torch.Size([2, 16, 20])
'''
  • 自然语言处理中，常见流程将经过词嵌入处理的词向量输入循环神经网络，得到隐层状态后再输入全连接层等后续处理。
self.embedding = nn.Embedding(n_vocab,emb_dims)
self.rnn = nn.RNN(emb_dims,h_out,n_l)
self.fc = nn.Linear(h_out,n_class)

LSTM.

  • 清楚基本 R N N rm RNN RNN 单元的计算过程及其在 P y T o r c h rm PyTorch PyTorch 中的具体使用方法后，理解 L S T M rm LSTM LSTM 就容易很多。 L S T M rm LSTM LSTM 全称 L o n g   S h o r t − T e r m   M e m o r y rm Long~Short-Term~Memory Long Short−Term Memory，译为长短期记忆网络，由 H o c h r e i t e r rm Hochreiter Hochreiter 和 S c h m i d h u b e r rm Schmidhuber Schmidhuber 于 1997 1997 1997 年提出，是针对标准 R N N rm RNN RNN 中长期记忆不能很好这一问题做出改进的复杂循环神经网络。
  • 更确切的说，长期记忆问题的出现是由于 R N N rm RNN RNN 中大跨度时间 t 1 , t 2 t_1,t_2 t1​,t2​ 对应梯度之间的依赖关系几乎不存在导致的。这也是所谓的循环神经网络梯度消失问题，这里的梯度消失并不是说梯度真的会趋近于零，而是和前时刻的关系变得越来越微弱，导致序列长度增大时，整个网络的结果不佳。例如下面这两个定语从句： T h e   c a t , w h i c h   a t e   l o t s   o f   c a t − f o o d , w a s   f u l l . rm The~cat,which~ate~lots~of~cat-food,was~full. The cat,which ate lots of cat−food,was full. T h e   c a t s , w h i c h   a t e   l o t s   o f   c a t − f o o d , w e r e   f u l l . rm The~cats,which~ate~lots~of~cat-food,were~full. The cats,which ate lots of cat−food,were full.
  • 如果需要对 w a s , w e r e rm was,were was,were 进行预测，那么影响关系最强的单词就是前面的 c a t , c a t s rm cat,cats cat,cats，但我们知道中间的定语从句可以继续扩展，而非上面所示的五个单词。 c a t − w a s , c a t s − w e r e rm cat-was,cats-were cat−was,cats−were 之间相距过远的后果就是二者依赖关系微弱，记普通循环神经网络无法很好地保持长期记忆。 L S T M rm LSTM LSTM 通过引入门控单元，来加强远距离依赖关系的保持，从而一定程度上增强长期记忆。

基本结构.

  • 下图是 C o l a h rm Colah Colah 一篇传播很广的 B l o g − 《 U n d e r s t a n d i n g   L S T M   N e t w o r k s 》 rm Blog-《Understanding~LSTM~Networks》 Blog−《Understanding LSTM Networks》 中展示的 L S T M rm LSTM LSTM 单元：
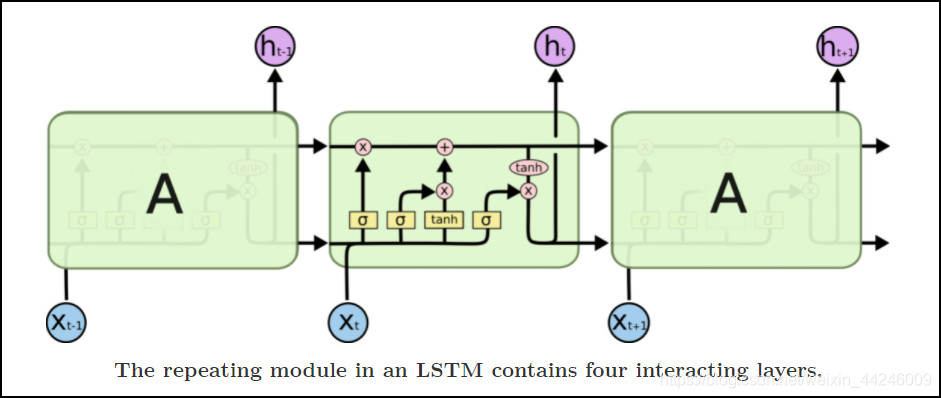
    在这里插入图片描述
  • 但我个人更习惯从公式出发来理清 L S T M rm LSTM LSTM 单元的计算规则，和 ( 3 ) (3) (3) 类似， L S T M rm LSTM LSTM 中也计算一个相同形式的量 g t g_t gt​，作为最终隐层状态 h t h_t ht​ 的一部分。其计算规则如下： g t = tanh ⁡ ( W i g x t + b i g + W h g h t − 1 + b h g ) (6.1) g_t=tanhbig(W_{ig}x_t+b_{ig}+W_{hg}h_{t-1}+b_{hg}big)tag{6.1} gt​=tanh(Wig​xt​+big​+Whg​ht−1​+bhg​)(6.1)隐层状态 h t h_t ht​ 的计算规则如下： h t = o t ⊙ tanh ⁡ ( c t ) (6.2) h_t=o_todottanh(c_t)tag{6.2} ht​=ot​⊙tanh(ct​)(6.2)其中 c t c_t ct​ 称为记忆单元，是 c e l l rm cell cell 的首字母简写，它负责计算过往信息与当下信息的加权关系，其计算规则如下： c t = f t ⊙ c t − 1 + i t ⊙ g t (6.3) c_t=f_todot c_{t-1}+i_todot g_ttag{6.3} ct​=ft​⊙ct−1​+it​⊙gt​(6.3)至此未给出定义的量还有 i t , f t , o t i_t,f_t,o_t it​,ft​,ot​，它们是 L S T M rm LSTM LSTM 中引入的三个门控，分别对应输入门 i n p u t rm input input，遗忘门 f o r g e t rm forget forget 和输出门 o u t p u t . rm output. output. 它们的计算规则完全一致，如下所示： i t = σ ( W i i x t + b i i + W h i h t − 1 + b h i ) (6.4) i_t=sigmabig(W_{ii}x_t+b_{ii}+W_{hi}h_{t-1}+b_{hi}big)tag{6.4} it​=σ(Wii​xt​+bii​+Whi​ht−1​+bhi​)(6.4) f t = σ ( W i f x t + b i f + W h f h t − 1 + b h f ) (6.5) f_t=sigmabig(W_{if}x_t+b_{if}+W_{hf}h_{t-1}+b_{hf}big)tag{6.5} ft​=σ(Wif​xt​+bif​+Whf​ht−1​+bhf​)(6.5) o t = σ ( W i o x t + b i o + W h o h t − 1 + b h i ) (6.6) o_t=sigmabig(W_{io}x_t+b_{io}+W_{ho}h_{t-1}+b_{hi}big)tag{6.6} ot​=σ(Wio​xt​+bio​+Who​ht−1​+bhi​)(6.6)
  • 从 L S T M rm LSTM LSTM 的图示中可以看到，在不同时刻之间传递的量是 c t , h t c_t,h_t ct​,ht​，并且在上方是 c t c_t ct​ 的传递流，下方是 h t h_t ht​ 的传递流，后面的代码中可以看到， c 0 , h 0 c_0,h_0 c0​,h0​ 是需要人为给定的。

PyTorch - LSTM.

构造参数.

  • 构造 P y T o r c h − L S T M rm PyTorch-LSTM PyTorch−LSTM 时需要的参数如下所示：
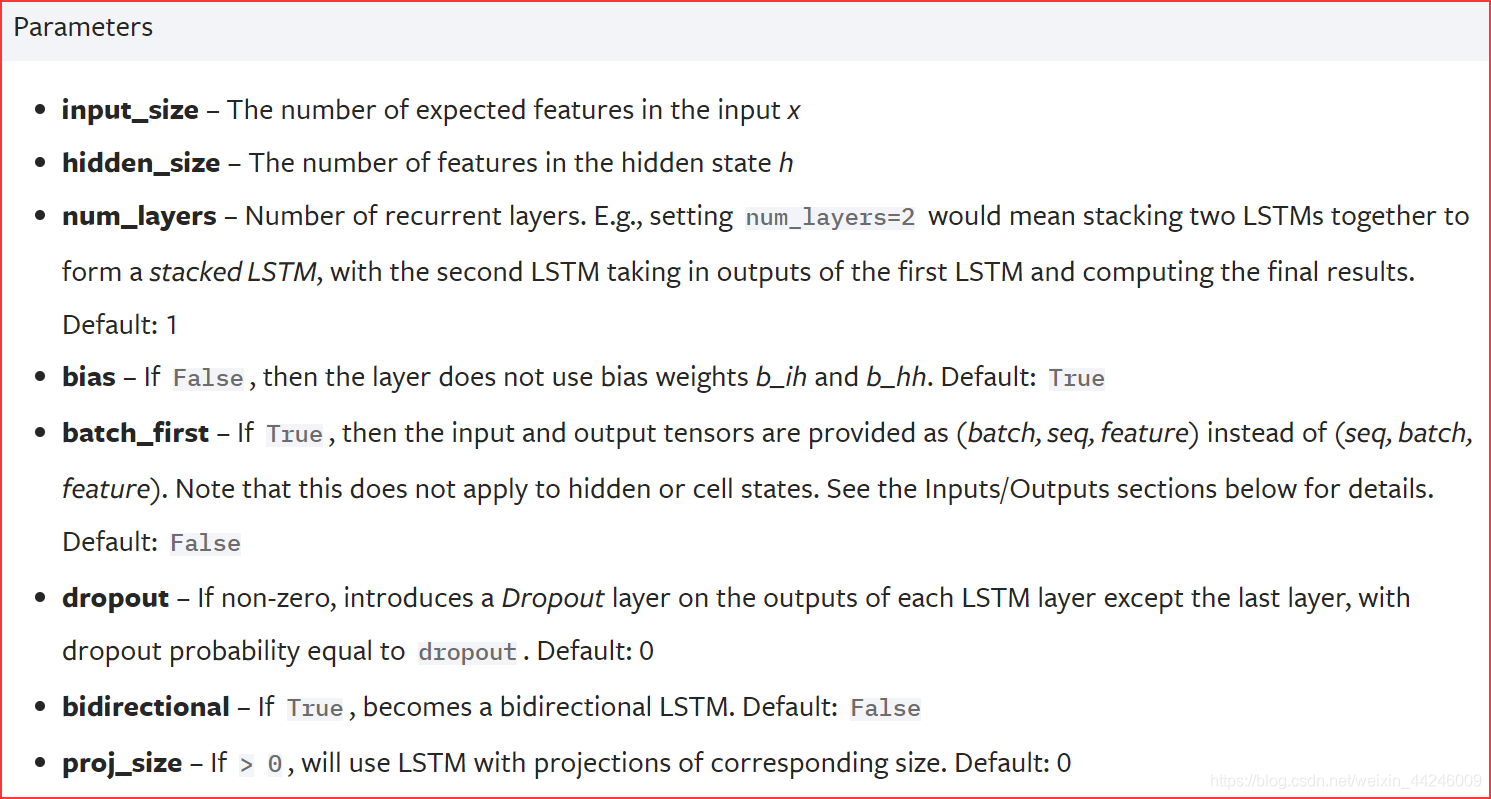
    在这里插入图片描述
  • 构造参数基本与简单 R N N rm RNN RNN 一致，重复的参数不再赘述。其中有两个参数是简单 R N N rm RNN RNN 所没有的 —— d r o p o u t , p r o j _ s i z e . rm dropout,proj_size. dropout,proj_size.
  • d r o p o u t rm dropout dropout 默认关闭，开启后会在多层 L S T M rm LSTM LSTM 网络中引入 d r o p o u t rm dropout dropout，除了最后一层不受影响，该参数的值就是输出被乘以 0 0 0 的概率。
    在这里插入图片描述
  • p r o j _ s i z e rm proj_size proj_size 默认关闭，开启后会将 h t h_t ht​ 的最后一个维度经过投影 h t = W h r h t h_t=W_{hr}h_t ht​=Whr​ht​ 后变为 p r o j _ s i z e rm proj_size proj_size，并且投影矩阵 W h r W_{hr} Whr​ 是可学习的。
    在这里插入图片描述

输入参数.

  • 可以预见的， L S T M rm LSTM LSTM 的输入参数会多于基本 R N N rm RNN RNN，首先是输入数据 i n p u t rm input input，而后是 c t , h t c_t,h_t ct​,ht​ 的初始值。
  • i n p u t rm input input 的维度和基本 R N N rm RNN RNN 中一致 —— [ L , N , H i n ] [L,N,H_{in}] [L,N,Hin​]，其中 L L L 是序列长度， N N N 的批大小， H i n H_{in} Hin​ 是输入维度大小。
  • h 0 , c 0 h_0,c_0 h0​,c0​ 的维度均为 [ N l , N , H o u t ] [N_l,N,H_{out}] [Nl​,N,Hout​]，这里暂时不考虑参数 p r o j _ s i z e rm proj_size proj_size 对于 h t h_t ht​ 的影响， N l N_l Nl​ 是网络中隐层层数。
  • 值得一提的是，在编码中需要将 h 0 , c 0 h_0,c_0 h0​,c0​ 组织成元组形式输入，即 ( h 0 , c 0 ) . (h_0,c_0). (h0​,c0​).

输出参数.

  • 和基本 R N N rm RNN RNN 一致， L S T M rm LSTM LSTM 会输出所有时刻 t t t 最后一个隐层的状态 h t h_t ht​ 张量，其维度是 [ L , N , H o u t ] . [L,N,H_{out}]. [L,N,Hout​].
  • 第二部分是元组 ( h n , c n ) (h_n,c_n) (hn​,cn​)，包含最后时刻所有隐层的隐层状态，二者的维度均为 [ N l , N , H o u t ] . [N_l,N,H_{out}]. [Nl​,N,Hout​].

代码示例.

  • 观察输入数据维度，初始隐层状态维度以及输出数据维度。
# In[Import]
import torch
import torch.nn as nn

# In[LSTM]
H_in = 300
H_out = hidden_size = 50
N_l = 2
lstm = nn.LSTM(H_in,hidden_size,N_l)

# In[Data]
L = 20
N = 32
x = torch.randn(L,N,H_in)
h_0 = torch.randn(N_l,N,H_out)
c_0 = torch.randn(N_l,N,H_out)

# In[Cal]
output,(h_n,c_n) = lstm(x,(h_0,c_0))
print('output.size:',output.size())
print('h_n size:',h_n.size())
print('c_n size:',c_n.size())

'''
output.size: torch.Size([20, 32, 50])
h_n size: torch.Size([2, 32, 50])
c_n size: torch.Size([2, 32, 50])
'''

GRU.

  • 通过最简单的 R N N rm RNN RNN 来理清循环神经网络计算的大体流程后，又介绍了引入复杂门控运算的 L S T M rm LSTM LSTM，再来看 G R U rm GRU GRU 就会相对轻松。
  • G R U rm GRU GRU 可以视为 L S T M rm LSTM LSTM 的简化版本，全称 G a t e d   R e c u r r e n t   U n i t rm Gated~Recurrent~Unit Gated Recurrent Unit，提出时间是 2014 2014 2014 年，已经有了前两个部分作为基础，这里就直接给出计算规则。
  • 首先同样会计算一个量 n t n_t nt​ 作为最终隐层状态 h t h_t ht​ 的部分，计算规则如下： n t = tanh ⁡ ( W i n x t + b i n + r t ⊙ ( W h n h t − 1 + b h n ) ) (7.1) n_t=tanhBig(W_{in}x_t+b_{in}+r_todotbig(W_{hn}h_{t-1}+b_{hn}big)Big)tag{7.1} nt​=tanh(Win​xt​+bin​+rt​⊙(Whn​ht−1​+bhn​))(7.1)其中 h t h_t ht​ 就是 G R U rm GRU GRU 中的隐层状态，计算规则如下： h t = ( 1 − z t ) ⊙ n t + z t ⊙ h t − 1 (7.2) h_t=(1-z_t)odot n_t+z_todot h_{t-1}tag{7.2} ht​=(1−zt​)⊙nt​+zt​⊙ht−1​(7.2)至此未给出定义的量还有 r t , z t r_t,z_t rt​,zt​，在 G R U rm GRU GRU 中分别称为重置门 r e s e t rm reset reset 和更新门 u p d a t e rm update update，它们的计算规则一致，如下所示： r t = σ ( W i r x t + b i r + W h r h t − 1 + b h r ) (7.3) r_t=sigmabig(W_{ir}x_t+b_{ir}+W_{hr}h_{t-1}+b_{hr}big)tag{7.3} rt​=σ(Wir​xt​+bir​+Whr​ht−1​+bhr​)(7.3) z t = σ ( W i z x t + b i z + W h z h t − 1 + b h z ) (7.4) z_t=sigmabig(W_{iz}x_t+b_{iz}+W_{hz}h_{t-1}+b_{hz}big)tag{7.4} zt​=σ(Wiz​xt​+biz​+Whz​ht−1​+bhz​)(7.4)
  • G R U rm GRU GRU 将 L S T M rm LSTM LSTM 中的三个门控简化为两个，并且没有记忆单元 c t c_t ct​ 在网络时间流中传递。 P y T o r c h − G R U rm PyTorch-GRU PyTorch−GRU 的构造参数如下所示：
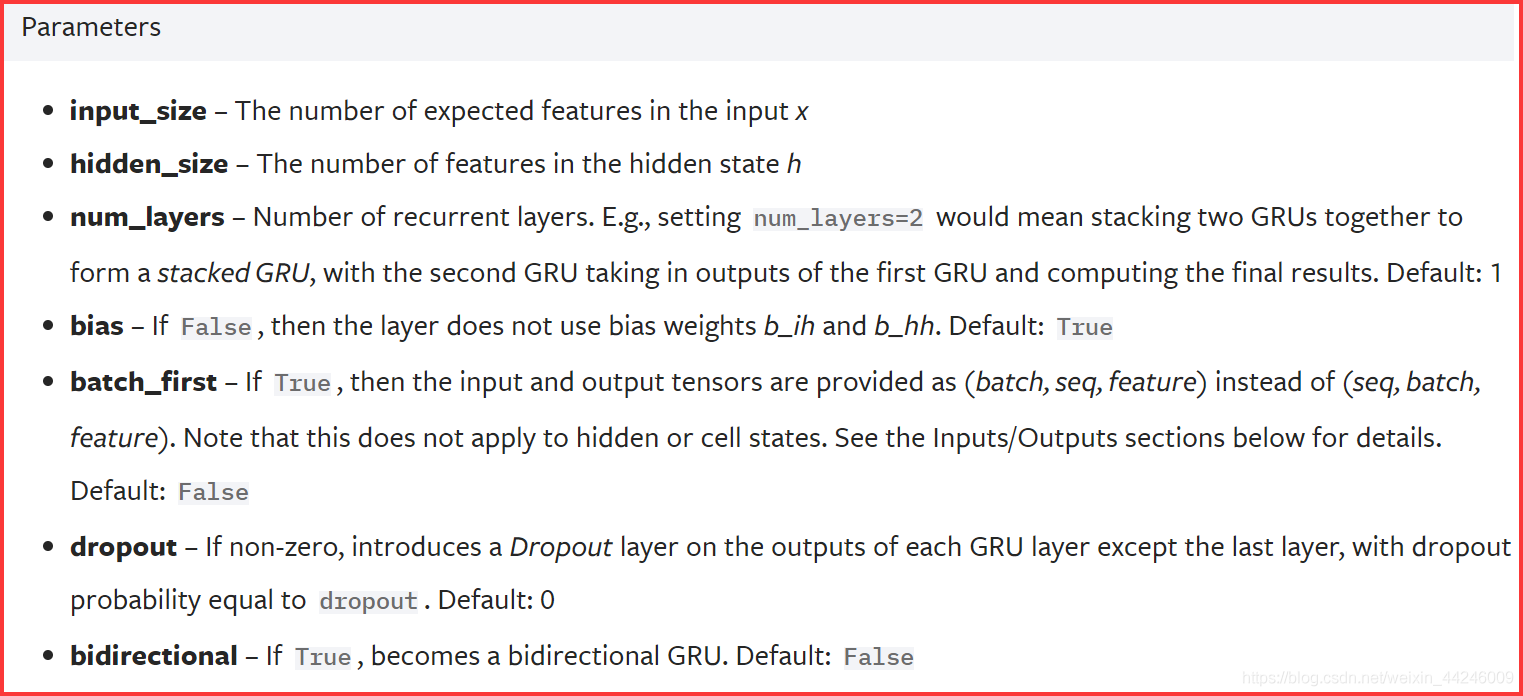
    在这里插入图片描述
  • P y T r o c h − G R U rm PyTroch-GRU PyTroch−GRU 的输入参数、输出参数均与标准 R N N rm RNN RNN 一致，代码示例如下：
# In[Import]
import torch
import torch.nn as nn

# In[GRU]
H_in = 50
hidden_size = H_out = 20
N_l = 2
gru = nn.GRU(H_in,hidden_size,N_l)

# In[Data]
L = 30
N = 64
x = torch.randn(L,N,H_in)
h_0 = torch.randn(N_l,N,H_out)

# In[Cal]
output,h_n = gru(x)
print('output.size:',output.size())
print('h_n.size:',h_n.size())

'''
output.size: torch.Size([30, 64, 20])
h_n.size: torch.Size([2, 64, 20])
'''

参考资料.

  • Understanding LSTM Networks
  • Understanding LSTM Networks 译文 —— 理解 LSTM 网络
  • RNN两种网络类型（Jordan network和Elman network）区别
  • pytorch中RNN参数的详细解释
  • 史上最详细循环神经网络讲解（RNN/LSTM/GRU —— (已断更，内容到 L S T M rm LSTM LSTM概述)
    在这里插入图片描述

最后

以上就是懦弱月光为你收集整理的【PyTorch】RNN/LSTM/GRU 计算过程、参数以及使用RNN.LSTM.GRU.参考资料.的全部内容，希望文章能够帮你解决【PyTorch】RNN/LSTM/GRU 计算过程、参数以及使用RNN.LSTM.GRU.参考资料.所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。

本图文内容来源于网友提供，作为学习参考使用，或来自网络收集整理，版权属于原作者所有。
点赞(42)

相关文章

lecture7-序列模型及递归神经网络RNN
lecture7-序列模型及递归神经网络RNN
RNN循环神经网络（过程解析）
RNN循环神经网络（过程解析）
【C语言基础】一直接收键盘字符 （while 循环，if条件语句）
【C语言基础】一直接收键盘字符 （while 循环，if条件语句）
if 和 while 语句的区别。
if 和 while 语句的区别。
【PyTorch】RNN/LSTM/GRU 计算过程、参数以及使用RNN.LSTM.GRU.参考资料.
【PyTorch】RNN/LSTM/GRU 计算过程、参数以及使用RNN.LSTM.GRU.参考资料.
while和if的区别及死循环如何产生？
while和if的区别及死循环如何产生？
计算机学习 DAY 17 - C - while循环小程序的实现
计算机学习 DAY 17 - C - while循环小程序的实现
C语言简单while循环while循环
C语言简单while循环while循环

评论列表共有 0 条评论

立即
投稿
返回
顶部