【算法与数据结构】二叉树（二叉树遍历、递归与非递归实现先中后序遍历、层次遍历）树的知识点二叉树小结：

71 阅读 0 评论 47 点赞

我是靠谱客的博主儒雅棒球，最近开发中收集的这篇文章主要介绍【算法与数据结构】二叉树（二叉树遍历、递归与非递归实现先中后序遍历、层次遍历）树的知识点二叉树小结：，觉得挺不错的，现在分享给大家，希望可以做个参考。

概述

二叉树

树的知识点
- 1.1名词解释
二叉树
- 2.1二叉树的性质
- - 2.1.1性质
  - 2.1.2存储结构
- 2.2 二叉树遍历
- - 2.2.1递归实现三种遍历
  - - 升级二推一
    - - 1.先序和中序推后序
      - 2.中序和后序推先序
  - 2.2.2非递归实现三种遍历
  - - 二叉树遍历——栈实现
    - 层次遍历—— 队列实现
小结：

树的知识点

1.1名词解释

1.节点的度: 一个节点含有的子树的个数称为该节点的度;
2.树的度: 一棵树中，最大的节点的度称为树的度;
3.叶节点或终端节点: 度为的节点;
4.非终端节点或分支节点: 度不为零的节点;
5.父亲节点或父节点: 若-一个节点含有子节点，则这个节点称为其子节点的父节点;
6.孩子节点或子节点: 一个节点含有的子树的根节点称为该节点的子节点;
7，兄弟节点: 具有相同父节点的节点互称为兄弟节点;
8.节点的层次: 从根开始定义起，根为第1层，根的子节点为第2层，以此类推;
9.深度: 对于任意节点n,n的深度为从根到n的唯一路径长, 根的深度为0;
10.高度:对于任意节点n,n的高度为从n到- -片树叶的最长路径长,所有树叶的高度为0;
11.堂兄弟节点:父节点在同一层的节点互为堂兄弟;
12.节点的祖先:从根到该节点所经分支上的所有节点;
13.子孙:以某节点为恨的子树中任一节点都称为该节点的子孙q
14. 森林:由m (m>=0)棵互不相交的树的集合称为森林;
15.树中任意节点的子节点之间没有顺序关系，这种树称为无序树，也称为自由树。反之是有序树。

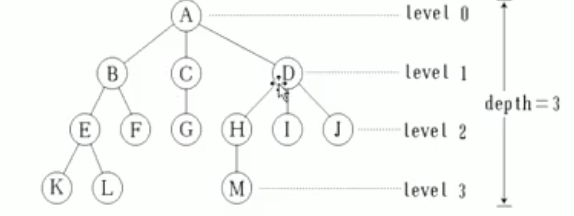
在这里插入图片描述

二叉树

2.1二叉树的性质

2.1.1性质

●若二叉树的层次从0开始则在二叉树的第i层最多有2i个结点。(i>= 0) [证明用数学归纳法
●高度为k的二叉树最多有2*+1-1个结点。 (k>= -1) [证明用求等比级数前 k项和的公式
●对任何一棵二叉树如果其叶结点个数为n0,度为2的非叶结点个数为n2,则有n0=n2+ 1.
定义:满二叉树(Full Binary Tree):每一个层的结点数都达到最大值，则这个二叉树就是满二叉树。
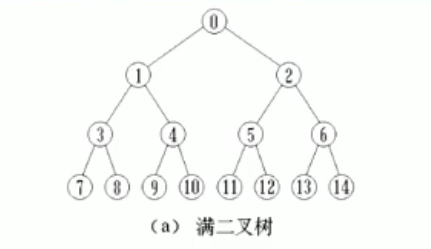
在这里插入图片描述
定义:完全二叉树(Complete Binary Tree):若设二叉树的高度为h,则共有h+1层。除第h层外，其它各层(0 - h- 1)的结点数部达到最大个数，第h层从右向左连续缺若干结点，这就是完全二叉树。

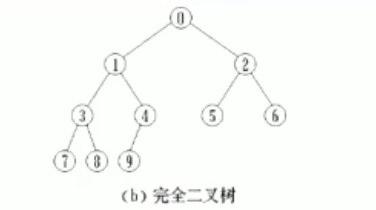
●具有n 个结点的完全二叉树的高度为「log2(n+1)7 -1
证明:设完全二叉树的高度为h，则有2^h-1<n≤^(2h+1)-1 => 2^h<n+1≤2^h+1=>取对数h< log2^(n+1)<= h+1

2.1.2存储结构

●数据元素之间的关系有两种不同的表示方法: 顺序映象和非顺序映象,并由此得到两种不同的存储
结构:顺序存储结构和链式存储结构。数据的存储结构是指数据的逻辑结构在计算机中的表示。
1.顺序存储表示：
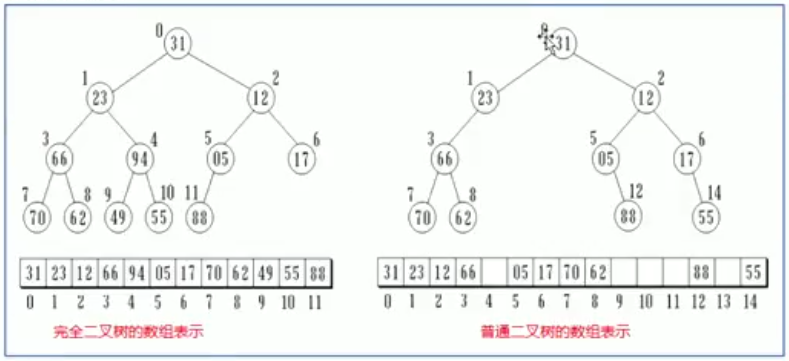
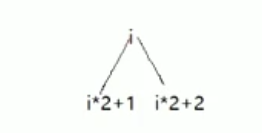
在这里插入图片描述

2.链式存储表示
满二叉树与完全二叉树适合用数组进行顺序存储，不浪费空间，如果普通二叉树用数组存储的话太浪费内存，数组有好多空缺，所以使用链式存储形式。
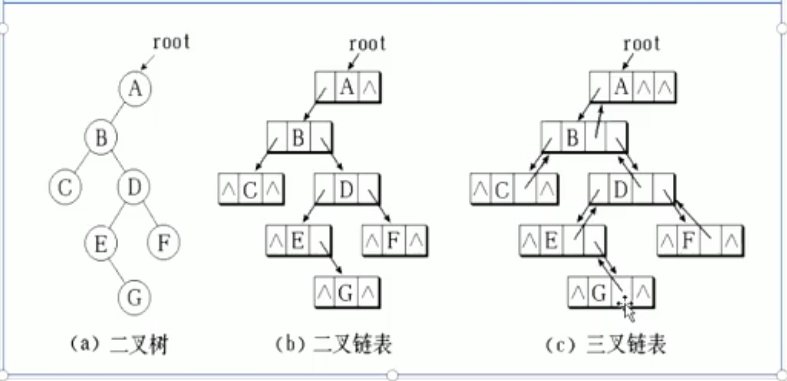
在这里插入图片描述
3.二叉链表的静态结构

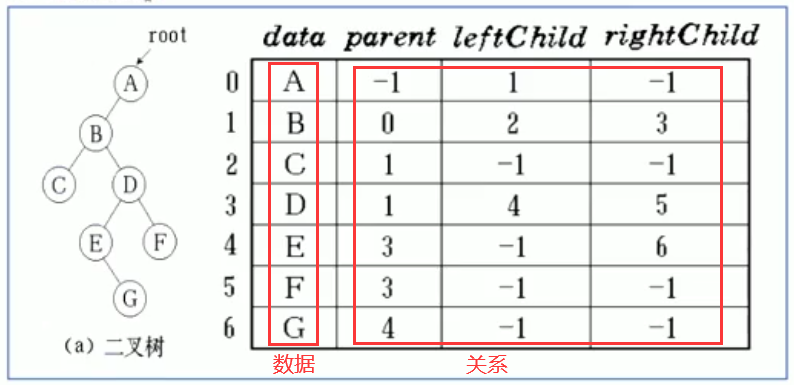
在这里插入图片描述

2.2 二叉树遍历

二叉树遍历(Binary Tree Traversal)，所谓树的遍历，就是按某种次序访问树中的结点，要求每个结点访问一次且仅访问一次。
设访问根结点记作V;
遍历根的左子树记作L;
遍历根的右子树记作 R;

则可能的遍历次序有:

遍历方法	表示	镜像	表示
前序	VLR	镜像	VRL
中序	LVR	镜像	RVL
后序	LRV	镜像	RLV

做个题：
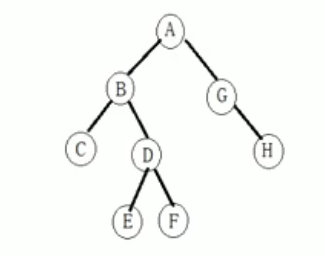
在这里插入图片描述
前序遍历：ABCDEFGH
中序遍历：CBEDFAGH
后序遍历：CEFDBHGA
代码讲解：
使用链式存储，递归实现二叉树的遍历
代码头

#include<stack>
#include<queue>
#include<list>
#include<unordered_map>
#include<stdlib.h>
#include<algorithm>
#include<iostream>

using namespace std;

#define END '#'
typedef char ElemType;
/*//三叉链表的定义
typedef struct BtNode
{
	BtNode* leftchild;
	BtNode* parent;
	BtNode* rightchild;
	ElemType data;
};
*/
//二叉
typedef struct BtNode
{
	BtNode* leftchild;
	//BtNode* parent;
	BtNode* rightchild;
	ElemType data;
}BtNode, * BinaryTree;;

//买节点操作
BtNode*  Buynode() { 
	BtNode* s = (BtNode*)malloc(sizeof(BtNode));
	if (NULL == s) 
		exit(1);//弄死它
	memset(s, 0, sizeof(BtNode));//s 的值变为 0
	return s;
}

定义一个结构体。
定义一个买节点的函数。

2.2.1递归实现三种遍历

typedef struct BtNode
{
	BtNode* leftchild;
	BtNode* rightchild;
	ElemType data;
}BtNode, * BinaryTree;;

//前序遍历
void PreOrder(BtNode* ptr) {
	if (ptr != NULL) {
		cout << ptr->data;
		PreOrder(ptr->leftchild);
		PreOrder(ptr->rightchild);
	}
}
//中序遍历
void InOrder(BtNode* ptr) {
	if (ptr != NULL) {
		InOrder(ptr->leftchild);
		cout << ptr->data;
		InOrder(ptr->rightchild);
	}
}
//后序遍历
void PastOrder(BtNode* ptr) {
	if (ptr != NULL) {
		PastOrder(ptr->leftchild);
		PastOrder(ptr->rightchild);
		cout << ptr->data;
	}
}

//创建一个二叉树
BtNode* CreateTree() {

	ElemType ch;
	BtNode* s = NULL;
	cin >> ch; 
	if (ch != END) {
		s = Buynode(); //购买一个节点
		s->data = ch;
		s->leftchild = CreateTree();
		s->rightchild = CreateTree();
	}
	return s;
}

int main() {

	//输入 ABC##DE##F##G3H##
	BinaryTree root = NULL;
	root = CreateTree();
	PreOrder(root);
	cout <<endl;
	InOrder(root);
	cout << endl;
	PastOrder(root);
	cout << endl;
	return 0;
}

升级二推一

这基本太简单，一般出题都是二推一，
给出先序和中序推后序
给出中序和后序推先序
但先序和后序无法推中序（无法确定根节点，并且会出现多种情况）
接下来看代码。

1.先序和中序推后序

//寻找pos 在中序中寻找这个值
int FindPos(const char* is, int n, ElemType val) {
	int pos = -1;
	for (int i = 0; i < n; i++) {
		if (is[i] == val) {
			pos = i;//返回它的下标
			break;
		}
	}
	return pos;
}

// 先序和中序推后续
BtNode* CreatePI(const char* ps, const char* is, int n) {
	BtNode* s = NULL;
	if (n > 0) {
		s = Buynode();//购买一个节点
		s->data = ps[0];
		int pos = FindPos(is, n, ps[0]);// 寻找pos
		if (pos == -1)exit(1);// 如果没找到  终止程序
		s->leftchild = CreatePI(ps + 1, is, pos);// pos 数据变小 
		s->rightchild = CreatePI(ps + 1+pos, is+1+pos, n-1-pos);//从树根节点后面的数据进行
	}
	return s;
}

BtNode* CreateBTreePI(const char* ps,const char* is, int n) {
	if (ps == NULL || is == NULL || n < 1) {
		return NULL;
	}
	else return CreatePI(ps, is, n);
}

2.中序和后序推先序

//寻找pos 在中序中寻找这个值
int FindPos(const char* is, int n, ElemType val) {
	int pos = -1;
	for (int i = 0; i < n; i++) {
		if (is[i] == val) {
			pos = i;//返回它的下标
			break;
		}
	}
	return pos;
}

//中序和后序推先序
BtNode* CreateIL(const char* is, const char* ls, int n) {
	BtNode* s = NULL;
	if (n > 0) {
		s = Buynode();
		s->data = ls[n - 1];
		int pos = FindPos(is, n, ls[n - 1]);
		if (pos == -1)exit(1);
		s->leftchild = CreateIL( is, ls,pos );
		s->rightchild = CreateIL( is+pos+1,ls+pos ,n-pos-1 );
	}
	return s;
}

//创建二叉树
BtNode* CreateBTreeIL(const char* ls, const char* is, int  n) {
	if (ls == NULL || is == NULL || n < 1) {
		return NULL;
	}
	else return CreateIL(ls, is, n);
}

实现递归遍历并不能满足我们的需求，再看非递归实现

2.2.2非递归实现三种遍历

二叉树遍历——栈实现

代码：

/*
* 
* 使用栈实现
*/

// 先序遍历非递归
void NicePreOrder(BtNode* ptr)
{
	if (ptr == NULL) return;
	stack<BtNode*> st; // 使用栈
	st.push(ptr);
	while (!st.empty())
	{
		ptr = st.top(); st.pop();
		cout << ptr->data << " ";
		if (ptr->rightchild != NULL)
			st.push(ptr->rightchild);
		if (ptr->leftchild  != NULL)
			st.push(ptr->leftchild );
	}
	cout << endl;
}
// 中序遍历非递归
void NiceInOrder(BtNode* ptr)
{
	if (ptr == NULL) return;
	stack<BtNode*> st; // 使用栈
	while (!st.empty() || ptr !=NULL )
	{
		while (ptr != NULL)
		{
			st.push(ptr);// 入栈
			ptr = ptr->leftchild;
		}
		ptr = st.top();//取栈顶指针
		st.pop();//出栈
		cout << ptr->data << " ";//输出
		ptr = ptr->rightchild;
	}
	cout << endl;
}
// 后序遍历非递归
void NicePastOrder(BtNode* ptr) 
{
	if (ptr == NULL) return;
	stack<BtNode*> st; // 使用栈
	BtNode* tag = NULL;
	while (!st.empty() || ptr != NULL)
	{
		while (ptr != NULL)
		{
			st.push(ptr);// 入栈
			ptr = ptr->leftchild;
		}
		ptr = st.top();//取栈顶指针
		st.pop();//出栈
		if (ptr->rightchild == NULL || ptr->rightchild == tag)
		{
			cout << ptr->data << " ";//输出
			tag = ptr;//tag 跟着打印出来的数据
			ptr = NULL;//注意  一定要为空！！！
		}
		else
		{
			st.push(ptr);
			ptr = ptr->rightchild;
		}
	}
	cout << endl;
}

层次遍历—— 队列实现

/*
使用层次遍历
 队列
*/

void NiceLevelOrder(BtNode* ptr) 
{
	if (ptr == NULL) return;
	queue<BtNode*> st; // 使用队列
	st.push(ptr);
	while (!st.empty())
	{
		ptr = st.front(); st.pop();
		cout << ptr->data << " ";

		if (ptr->leftchild != NULL)
			st.push(ptr->leftchild);
		if (ptr->rightchild != NULL)
			st.push(ptr->rightchild);
	}
	cout << endl;
}

附完整代码：
递归遍历

#include<stack>
#include<queue>
#include<list>
#include<unordered_map>
#include<stdlib.h>
#include<algorithm>
#include<iostream>

using namespace std;

#define END '#'
typedef char ElemType;
#if 1
/*//三叉链表的定义
typedef struct BtNode
{
	BtNode* leftchild;
	BtNode* parent;
	BtNode* rightchild;
	ElemType data;
};
*/
//二叉
typedef struct BtNode
{
	BtNode* leftchild;
	//BtNode* parent;
	BtNode* rightchild;
	ElemType data;
}BtNode, * BinaryTree;;


BtNode*  Buynode() {
	BtNode* s = (BtNode*)malloc(sizeof(BtNode));
	if (NULL == s) 
		exit(1);//弄死它
	memset(s, 0, sizeof(BtNode));//s 的值变为 0
	return s;
}


//前序遍历
void PreOrder(BtNode* ptr) {
	if (ptr != NULL) {
		cout << ptr->data;
		PreOrder(ptr->leftchild);
		PreOrder(ptr->rightchild);
	}
}
//中序遍历
void InOrder(BtNode* ptr) {
	if (ptr != NULL) {
		InOrder(ptr->leftchild);
		cout << ptr->data;
		InOrder(ptr->rightchild);
	}
}
//后序遍历
void PastOrder(BtNode* ptr) {
	if (ptr != NULL) {
		PastOrder(ptr->leftchild);
		PastOrder(ptr->rightchild);
		cout << ptr->data;
	}
}

BtNode* CreateTree() {

	ElemType ch;
	BtNode* s = NULL;
	cin >> ch; 
	if (ch != END) {
		s = Buynode(); //购买一个节点
		s->data = ch;
		s->leftchild = CreateTree();
		s->rightchild = CreateTree();
	}
	return s;
}
#if 0
int main() {

	//输入 ABC##DE##F##G3H##
	BinaryTree root = NULL;
	root = CreateTree();
	PreOrder(root);
	cout <<endl;
	InOrder(root);
	cout << endl;
	PastOrder(root);
	cout << endl;
	return 0;
}
#endif

//寻找pos 在中序中寻找这个值
int FindPos(const char* is, int n, ElemType val) {
	int pos = -1;
	for (int i = 0; i < n; i++) {
		if (is[i] == val) {
			pos = i;//返回它的下标
			break;
		}
	}
	return pos;
}
// 先序和中序推后续
BtNode* CreatePI(const char* ps, const char* is, int n) {
	BtNode* s = NULL;
	if (n > 0) {
		s = Buynode();//购买一个节点
		s->data = ps[0];
		int pos = FindPos(is, n, ps[0]);// 寻找pos
		if (pos == -1)exit(1);// 如果没找到  终止程序
		s->leftchild = CreatePI(ps + 1, is, pos);// pos 数据变小 
		s->rightchild = CreatePI(ps + 1+pos, is+1+pos, n-1-pos);//从树根节点后面的数据进行
	}
	return s;
}

//实现不了先序和后序推中序
BtNode* CreatePL(const char* ps, const char* ls, int n) {
	BtNode* s = NULL;
	if (n > 0) {
		s = Buynode();
		s->data = ps[0];
		int pos = FindPos(ls, n, ps[0]);
		if (pos == -1)exit(1);
		s->leftchild = CreatePL(ps+1,ls ,pos );
		s->rightchild = CreatePL(ps+pos+1 ,ls+pos ,n-pos -1);
	}
	return s;
}


//中序和后序推先序
BtNode* CreateIL(const char* is, const char* ls, int n) {
	BtNode* s = NULL;
	if (n > 0) {
		s = Buynode();
		s->data = ls[n - 1];
		int pos = FindPos(is, n, ls[n - 1]);
		if (pos == -1)exit(1);
		s->leftchild = CreateIL( is, ls,pos );
		s->rightchild = CreateIL( is+pos+1,ls+pos ,n-pos-1 );
	}
	return s;
}

//创建二叉树
BtNode* CreateBTreePI(const char* ps,const char* is, int n) {
	if (ps == NULL || is == NULL || n < 1) {
		return NULL;
	}
	else return CreatePI(ps, is, n);
}

BtNode* CreateBTreePL(const char* ps, const char* ls, int  n) {
	if (ps == NULL ||ls == NULL || n < 1) {
		return NULL;
	}
	else return CreatePL(ps, ls, n);
}

BtNode* CreateBTreeIL(const char* ls, const char* is, int  n) {
	if (ls == NULL || is == NULL || n < 1) {
		return NULL;
	}
	else return CreateIL(ls, is, n);
}
int main() {
	const char ps[] = "ABCDEFGH";
	const char is[] = "CBEDFAGH";
	const char ls[] = "CEFDBHGA";

	int n = strlen(ps);

	BinaryTree root = NULL;
	//root = CreateBTreePI(ps,is, n);
	//root = CreateBTreePL(ps,ls, n);//不能根据先序和后序推中序
	//root = CreateBTreeIL(is,ls, n);

	PreOrder(root);
	cout << endl;
	InOrder(root);
	cout << endl;
	PastOrder(root);
	cout << endl;
}

#endif

非递归遍历

#include<stack>
#include<queue>
#include<list>
#include<unordered_map>
#include<stdlib.h>
#include<algorithm>
#include<iostream>

using namespace std;

#define END '#'
typedef char ElemType;

typedef struct BtNode
{
	BtNode* leftchild;
	//BtNode* parent;
	BtNode* rightchild;
	ElemType data;
}BtNode, * BinaryTree;;


BtNode* Buynode() {
	BtNode* s = (BtNode*)malloc(sizeof(BtNode));
	if (NULL == s)
		exit(1);//弄死它
	memset(s, 0, sizeof(BtNode));//s 的值变为 0
	return s;
}

//寻找pos 在中序中寻找这个值
int FindPos(const char* is, int n, ElemType val) {
	int pos = -1;
	for (int i = 0; i < n; i++) {
		if (is[i] == val) {
			pos = i;//返回它的下标
			break;
		}
	}
	return pos;
}

/*
* 
* 使用栈实现
*/

// 先序遍历非递归
void NicePreOrder(BtNode* ptr)
{
	if (ptr == NULL) return;
	stack<BtNode*> st; // 使用栈
	st.push(ptr);
	while (!st.empty())
	{
		ptr = st.top(); st.pop();
		cout << ptr->data << " ";
		if (ptr->rightchild != NULL)
			st.push(ptr->rightchild);
		if (ptr->leftchild  != NULL)
			st.push(ptr->leftchild );
	}
	cout << endl;
}
// 中序遍历非递归
void NiceInOrder(BtNode* ptr)
{
	if (ptr == NULL) return;
	stack<BtNode*> st; // 使用栈
	while (!st.empty() || ptr !=NULL )
	{
		while (ptr != NULL)
		{
			st.push(ptr);// 入栈
			ptr = ptr->leftchild;
		}
		ptr = st.top();//取栈顶指针
		st.pop();//出栈
		cout << ptr->data << " ";//输出
		ptr = ptr->rightchild;
	}
	cout << endl;
}
// 后序遍历非递归
void NicePastOrder(BtNode* ptr) 
{
	if (ptr == NULL) return;
	stack<BtNode*> st; // 使用栈
	BtNode* tag = NULL;
	while (!st.empty() || ptr != NULL)
	{
		while (ptr != NULL)
		{
			st.push(ptr);// 入栈
			ptr = ptr->leftchild;
		}
		ptr = st.top();//取栈顶指针
		st.pop();//出栈
		if (ptr->rightchild == NULL || ptr->rightchild == tag)
		{
			cout << ptr->data << " ";//输出
			tag = ptr;//tag 跟着打印出来的数据
			ptr = NULL;//注意  一定要为空！！！
		}
		else
		{
			st.push(ptr);
			ptr = ptr->rightchild;
		}
	}
	cout << endl;
}


/*
使用层次遍历
 队列
*/

void NiceLevelOrder(BtNode* ptr) 
{
	if (ptr == NULL) return;
	queue<BtNode*> st; // 使用队列
	st.push(ptr);
	while (!st.empty())
	{
		ptr = st.front(); st.pop();
		cout << ptr->data << " ";

		if (ptr->leftchild != NULL)
			st.push(ptr->leftchild);
		if (ptr->rightchild != NULL)
			st.push(ptr->rightchild);
	}
	cout << endl;
}

//中序和后序推先序
BtNode* CreateIL(const char* is, const char* ls, int n) {
	BtNode* s = NULL;
	if (n > 0) {
		s = Buynode();
		s->data = ls[n - 1];
		int pos = FindPos(is, n, ls[n - 1]);
		if (pos == -1)exit(1);
		s->leftchild = CreateIL(is, ls, pos);
		s->rightchild = CreateIL(is + pos + 1, ls + pos, n - pos - 1);
	}
	return s;
}

BtNode* CreateBTreeIL(const char* ls, const char* is, int  n) {
	if (ls == NULL || is == NULL || n < 1) {
		return NULL;
	}
	else return CreateIL(ls, is, n);
}

int main() {
	const char ps[] = "ABCDEFGH";
	const char is[] = "CBEDFAGH";
	const char ls[] = "CEFDBHGA";

	int n = strlen(ps);

	BinaryTree root = NULL;
	
	root = CreateBTreeIL(is,ls, n);
	NicePreOrder(root);
	NiceInOrder(root);
	NicePastOrder(root);
	NiceLevelOrder(root);// 层次遍历
	cout << endl;
}

小结：

1.现阶段二叉树的遍历就要求掌握三种：先序，中序，后序
二叉树的遍历还可以进行多样形式的遍历：

层次遍历（上面有提到）
s 型层次遍历.
反s 型层次遍历。
…

2.先序中序推后序，后序中序推前序，得记住前后不能推中。
3.熟悉掌握队列、栈、链表的使用，以及运行过程，解决二叉树不是问题。

最后

以上就是儒雅棒球为你收集整理的【算法与数据结构】二叉树（二叉树遍历、递归与非递归实现先中后序遍历、层次遍历）树的知识点二叉树小结：的全部内容，希望文章能够帮你解决【算法与数据结构】二叉树（二叉树遍历、递归与非递归实现先中后序遍历、层次遍历）树的知识点二叉树小结：所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。

本图文内容来源于网友提供，作为学习参考使用，或来自网络收集整理，版权属于原作者所有。

本文分类：c++
浏览次数：71 次浏览
发布日期：2024-05-15 21:00:02
本文链接：https://www.kaopuke.com/article/k-p-k_13_u_7_o_26_f0_13_j_6_0.html

常见小问题(待更新)1、求一组数中第K大或第K小的数2、求N的阶乘十进制数最后有多少个03、KMP(字符串模式匹配)4、二叉树建立与遍历5、求一个数组中连续子数组和最大或乘积最大6、约瑟夫环问题7、从n个数中等概率取m个数8、快速求（n^p)%m9、数组中求出现奇数次或一次的数10、求2000000以内的素数

【算法与数据结构】二叉树（二叉树遍历、递归与非递归实现先中后序遍历、层次遍历）树的知识点二叉树小结：

概述

二叉树

树的知识点

1.1名词解释

二叉树

2.1二叉树的性质

2.1.1性质

2.1.2存储结构

2.2 二叉树遍历

2.2.1递归实现三种遍历

升级二推一

1.先序和中序推后序

2.中序和后序推先序

2.2.2非递归实现三种遍历

二叉树遍历——栈实现

层次遍历—— 队列实现

小结：

最后

评论列表共有 0 条评论

发表评论取消回复

【算法与数据结构】二叉树 （二叉树遍历、递归与非递归实现先中后序遍历、层次遍历）树的知识点二叉树小结：

概述

二叉树

树的知识点

1.1名词解释

二叉树

2.1二叉树的性质

2.1.1性质

2.1.2存储结构

2.2 二叉树遍历

2.2.1递归实现三种遍历

升级二推一

1.先序和中序推后序

2.中序和后序推先序

2.2.2非递归实现三种遍历

二叉树遍历——栈实现

层次遍历—— 队列实现

小结：

最后

相关文章

评论列表共有 0 条评论

发表评论 取消回复

【算法与数据结构】二叉树（二叉树遍历、递归与非递归实现先中后序遍历、层次遍历）树的知识点二叉树小结：

发表评论取消回复