【数据结构】已知一棵二叉链表表示的二叉树T，编写函数，判断T是否为完全二叉树1.算法思想2.定义结构体3.函数实现4.测试结果5.完整代码

57 阅读 0 评论 38 点赞

我是靠谱客的博主默默毛豆，最近开发中收集的这篇文章主要介绍【数据结构】已知一棵二叉链表表示的二叉树T，编写函数，判断T是否为完全二叉树1.算法思想2.定义结构体3.函数实现4.测试结果5.完整代码，觉得挺不错的，现在分享给大家，希望可以做个参考。

概述

1.算法思想

根据完全二叉树定义，将队头元素出队并判断其左右孩子情况。根据不同情况来分析起是否为完全二叉树。

2.定义结构体

typedef struct BiNode {
    int data;
    struct BiNode* lchild;
    struct BiNode* rchild;
} BiNode,*BiTree;

3.函数实现

使用层序遍历+队列实现。首先根据队头结点判断其左右孩子是否存在，有如下情况：

左右孩子都存在：将左右孩子入队。
左孩子不存在，右孩子存在：很明显不满足完全二叉树的条件。
左孩子存在但右孩子不存在或左右孩子都不存在：前一种情况说明该结点是最后一个有孩子的结点，从该结点后的所有结点都是叶子结点。后一种情况说明当前结点就是第一个叶子结点，其后面所有结点都是叶子结点。

/*层序遍历+队列*/
bool check(BiTree T) {
    BiNode *Q[MAXSIZE];//队列
    BiNode *p;
    int front = -1, rear = -1;//队头和队尾
    Q[++rear] = T;//根结点入队
    while(front < rear) {
        p = Q[++front];//将队头结点出队，将其左右孩子入队
        //如果左右孩子都存在，则入队
        if(p->lchild && p->rchild) {
            Q[++rear] = p->lchild;
            Q[++rear] = p->rchild;
        } else if(!p->lchild && p->rchild) {
            //如果左孩子存在但右孩子不存在，肯定不是完全二叉树，返回false
            return false;
        }
        //否则左孩子存在但右孩子不存在或者左右孩子都不存在。
        //那么这个结点之后的结点一定都是叶子结点，因此从当前结点往后判断。
        else {
            //左孩子存在，将其入队
            if(p->lchild &&!p->rchild) {
                Q[++rear] = p->lchild;
            }
            //从当前结点开始判断，如果有非叶子结点，则返回false
            while(front < rear) {
                p = Q[++front];
                if(p->lchild || p->rchild) {
                    return false;
                }
            }
        }
    }
    return true;
}

4.测试结果

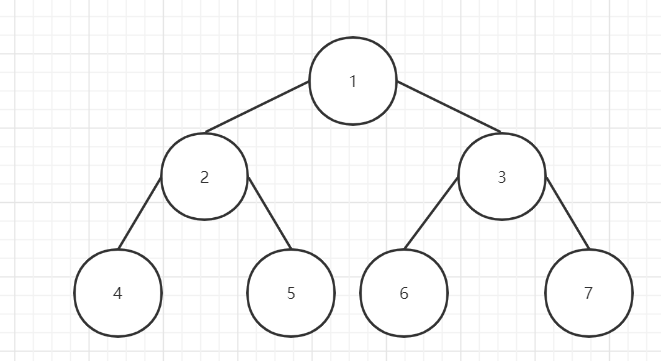
以如图所示的二叉树进行测试。将输出判定结果不是完全二叉树。
在这里插入图片描述

5.完整代码

#include <stdio.h>
#include <malloc.h>
#include <stdbool.h>
#define MAXSIZE 50

typedef struct BiNode {
    int data;
    struct BiNode* lchild;
    struct BiNode* rchild;
} BiNode,*BiTree;

/*层序遍历+队列*/
bool check(BiTree T) {
    BiNode *Q[MAXSIZE];//队列
    BiNode *p;
    int front = -1, rear = -1;//队头和队尾
    Q[++rear] = T;//根结点入队
    while(front < rear) {
        p = Q[++front];//将队头结点出队，将其左右孩子入队
        //如果左右孩子都存在，则入队
        if(p->lchild && p->rchild) {
            Q[++rear] = p->lchild;
            Q[++rear] = p->rchild;
        } else if(!p->lchild && p->rchild) {
            //如果左孩子存在但右孩子不存在，肯定不是完全二叉树，返回false
            return false;
        }
        //否则左孩子存在但右孩子不存在或者左右孩子都不存在。
        //那么这个结点之后的结点一定都是叶子结点，因此从当前结点往后判断。
        else {
            //左孩子存在，将其入队
            if(p->lchild &&!p->rchild) {
                Q[++rear] = p->lchild;
            }
            //从当前结点开始判断，如果有非叶子结点，则返回false
            while(front < rear) {
                p = Q[++front];
                if(p->lchild || p->rchild) {
                    return false;
                }
            }
        }
    }
    return true;
}

int main() {
    BiTree l1 = (BiTree)malloc(sizeof(BiNode));
    BiNode *l2 = (BiNode *)malloc(sizeof(BiNode));
    BiNode *l3 = (BiNode *)malloc(sizeof(BiNode));
    BiNode *l4 = (BiNode *)malloc(sizeof(BiNode));
    BiNode *l5 = (BiNode *)malloc(sizeof(BiNode));
    BiNode *l6 = (BiNode *)malloc(sizeof(BiNode));
    BiNode *l7 = (BiNode *)malloc(sizeof(BiNode));
    l1->data = 1;
    l2->data = 2;
    l3->data = 3;
    l4->data = 4;
    l5->data = 5;
    l6->data = 6;
    l7->data = 7;
    l1->lchild = l2;
    l1->rchild = l3;
    l2->lchild = l4;
    l2->rchild = l5;
    l3->lchild = l6;
    l3->rchild = l7;
    l4->lchild = NULL;
    l4->rchild = NULL;
    l5->lchild = NULL;
    l5->rchild = NULL;
    l6->lchild = NULL;
    l6->rchild = NULL;
    l7->lchild = NULL;
    l7->rchild = NULL;
    bool a = check(l1);
    if(a) {
        printf("该二叉树是完全二叉树n");
    } else {
        printf("该二叉树不是完全二叉树n");
    }
    return 0;
}