【数据结构】二叉树的概念及实现

66 阅读 0 评论 44 点赞

我是靠谱客的博主沉静学姐，最近开发中收集的这篇文章主要介绍【数据结构】二叉树的概念及实现，觉得挺不错的，现在分享给大家，希望可以做个参考。

概述

二叉树的定义：

二叉树T一个有穷的节点集合，这个集合可以为空，若不为空，则它由根节点和一个称为左子树TL 和右子树TR的两个完全不相交的二叉树组成。

二叉树的顺序存储分析：

完全二叉树：
若设二叉树的深度为h，除第h层外，其他各层（1~h-1）的节点数都达到最大个数，第h层所有节点都连续集中在最左边，这就是完全二叉树
满二叉树：
除最后一层无任何子节点外，每一层上的所有结点都有两个子结点。满二叉树一定是完全二叉树，不同的是最后一层的所有节点都有两个字节点。
对于一个完全二叉树如何用顺序存储实现呢？
我们可以对完全二叉树进行从上到下，从左到右编号，然后以编号为下标将节点的值依次放入一个数组中，这时候下标之间的规律们可以反映二叉树的层次关系（比如根据双亲节点的下标，找到其左孩子和右孩子的下标）：
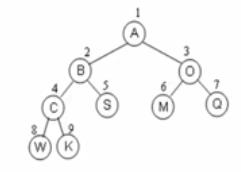
在这里插入图片描述

N个节点的完全二叉树的节点父子关系：
（1）非根节点，序号（i >1)父节点的序号为i/2；
（2）节点的序号为i，左孩子的序号为2 * i；
（3）节点的序号为i，右孩子的序号为2 * i + 1；
而对于非完全二叉树也可以用顺序存储的方法实现，空出来的节点序号为0；但是这样会浪费大量的存储空间；

二叉树的链式存储及实现：

#define Elemtype char 
#define Btree_Node STDataType
typedef struct Btree_Node{//二叉树节点的结构
	Elemtype data;
	Btree_Node* L_child;
	Btree_Node* R_child;
}Btree_Node;
typedef struct StackNode{//栈节点的结构
	STDataType* value; 
    struct StackNode *next;
}StackNode;
typedef struct QueueNode{//队列节点的结构
	STDataType* value;
	struct QueueNode* next;
}QueueNode;
typedef struct Queue{//队列的结构
	QueueNode* front;//队头
	QueueNode* rear;//队尾
}Queue;
//*******************栈的基本操作********************//
StackNode* StackInit();
void StackPush(StackNode**,STDataType*);
void StackPop(StackNode**);
STDataType* StackTop(StackNode* stack);
bool is_StackEmpty(StackNode* stack);
//*******************队列的基本操作****************//
Queue* QueueInit();// 创建队列
void QueuePush(Queue* q, STDataType* data);// 队尾入队列
void QueuePop(Queue* q);// 队头出队列
STDataType* QueueFront(Queue* q);// 获取队列头部元素
STDataType* Queuerear(Queue* q);// 获取队列队尾元素
bool is_QueueEmpty(Queue* q);// 检测队列是否为空
void QueueDestroy(Queue* q);// 销毁队列
//*******************二叉树的基本操作****************//
//创建一个完全二叉树
Btree_Node* Creat_BinTree();
//判断二叉树是否为空
bool is_empty_BinTree(Btree_Node*);
//生成一个节点
Btree_Node* Buy_New_Node(Elemtype data);
//销毁整个二叉树
void Free_tree(Btree_Node*);
//增加数据项到二叉树，即插入新的子树
void Insert_ChildTree(Btree_Node* ,Btree_Node* ,int n);
//n=1删除左子树，n=2删除右子树
void Delete_ChildTree(Btree_Node* ,int n);
//先序遍历的递归实现
void Pre_Order_BinTree(Btree_Node* ptr);
 //中序遍历的递归实现
void Mid_Order_BinTree(Btree_Node* ptr);
 //后序遍历的递归实现
void Post_Order_BinTree(Btree_Node* ptr);

//先序遍历的非递归实现
void NPre_Order_BinTree(Btree_Node* ptr);
 //中序遍历的非递归实现
void NMid_Order_BinTree(Btree_Node* ptr);
 //后序遍历的非递归实现
void NPost_Order_BinTree(Btree_Node* ptr);

/*******************层序遍历实现********/
void Level_Order_BinTree(Btree_Node* Ptr);

//*******************栈的基本操作********************//
StackNode* StackInit(){//栈的初始化
	StackNode* stack = NULL;
	return stack;
}
void StackPush(StackNode** stack,STDataType* data){
	assert(stack);
	StackNode* ptr = (StackNode*)malloc(sizeof(StackNode));
	ptr ->value = data; 
	ptr ->next = *stack;
	*stack = ptr;
}
void StackPop(StackNode** stack){
	if(is_StackEmpty(*stack)){
		printf("栈空n");
	}else{
		StackNode* ptr = (*stack);
		(*stack) = ptr ->next;
		free(ptr);
	}
}
STDataType* StackTop(StackNode* stack){
	assert(!is_StackEmpty(stack));
	return stack ->value;
}
bool is_StackEmpty(StackNode* stack){
	if(stack == NULL){
		return true;
	}else{
		return false;
	}
}
//*******************队列的基本操作****************//
Queue* QueueInit(){// 创建队列
	Queue* q = (Queue*)malloc(sizeof(Queue));
	q ->front = q ->rear =NULL;
	return q;
}
void QueuePush(Queue* q, STDataType* value){// 队尾入队列
	assert(q);//队列不存在
	QueueNode* ptr = (QueueNode*)malloc(sizeof(QueueNode));
	ptr ->value = value;
	ptr ->next = NULL;
	if(is_QueueEmpty(q)){//队列为空
		q ->front = q ->rear = ptr;
	}else{
		q ->rear ->next = ptr;
		q ->rear = ptr;
	}
}
void QueuePop(Queue* q){// 队头出队列
	if(is_QueueEmpty(q)){
		printf("队列空");
	}else{
		QueueNode* ptr = q ->front;
		q ->front =q ->front ->next;
		if(q ->front == NULL){
			q ->rear = q ->front;
		}
		free(ptr);
	}

}
STDataType* QueueFront(Queue* q){// 获取队列头部元素
	assert(q);
	if(is_QueueEmpty(q)){
		printf("队列空n");
	}else{
		return q ->front ->value;
	}
}
STDataType* Queuerear(Queue* q){// 获取队列队尾元素
	assert(q);
	if(is_QueueEmpty(q)){
		printf("队列空n");
	}else{
		return (q ->rear)->value;
	}
}
bool is_QueueEmpty(Queue* q){// 检测队列是否为空
	assert(q);
	if(q ->front == NULL){
		return  true;
	}else{
		return false;
	}
}
void QueueDestroy(Queue* q){// 销毁队列
	assert(q);
	while(!is_QueueEmpty(q)){
		QueuePop(q);
	}
	free(q);
}
//*******************二叉树的基本操作********************//
Btree_Node* Creat_BinTree(){//创建一个完全二叉树                                            
	Elemtype *a = (Elemtype*)malloc(sizeof(Elemtype) * 50);//字符数组
	scanf("%s",a);
	int leng = strlen(a);
	//为了之后能够删除单个节点，所以节点空间需要一个个申请，那么就需要一个数组record记录各节点的地址
	Btree_Node** record = (Btree_Node**)malloc(sizeof(Btree_Node*) * leng);
	for(int i = 0; i < leng;i++ ){
		Btree_Node* ptr = (Btree_Node*)malloc(sizeof(Btree_Node));
		record[i] = ptr;
		ptr ->data = a[i];
		ptr ->L_child = ptr ->R_child = NULL;
	}
	for(int i = 0; i < leng;i++){
		if(2*i+1 < leng){//有左孩子
			record[i] ->L_child = record[2 * i + 1];
		}
		if(2*i + 2 < leng){//有右孩子
			record[i] ->R_child = record[2 * i + 2];
		}
	}
	if(leng == 0){
		return NULL;
	}else{
		return record[0];
	}
	
}

bool is_empty_BinTree(Btree_Node* ptr){//判断二叉树是否为空
	if(ptr == NULL){
		return true; 
	}else{
		return false;
	}
}
Btree_Node* Buy_New_Node(Elemtype data){//生成一个节点
	Btree_Node* ptr = (Btree_Node*)malloc(sizeof(Btree_Node));
	ptr ->data = data;
	ptr ->L_child = NULL;
	ptr ->R_child = NULL;
	return ptr;
}
void Free_tree(Btree_Node* ptr){//销毁整个二叉树
	//后续遍历销毁整个二叉树
	if(ptr){
		Free_tree(ptr ->L_child);
		Free_tree(ptr ->R_child);
		free(ptr);
	}
	//注意形成的野指针；
}
//增加数据项到二叉树，即插入新的子树
void Insert_ChildTree(Btree_Node* ptr,Btree_Node* insert,int n){
	if(ptr){
		if(ptr ->L_child == NULL && n == 1 ){
			ptr ->L_child = insert;
		}else if(ptr ->R_child == NULL && n == 2){
			ptr ->R_child = insert;
		}else if(ptr ->L_child != NULL && n == 1 ){
			printf("左孩子不为空n");
		}else if(ptr ->R_child != NULL && n == 2){
			printf("右孩子不为空n");
		}
	}
}
//n=1删除左子树，n=2删除右子树
void Delete_ChildTree(Btree_Node* ptr,int n){
	if(ptr == NULL){
		printf("树为空n");
	}else{
		if(n == 1){
			Free_tree(ptr ->L_child);
			ptr ->L_child =NULL;//防止野指针的形成
		}else if(n == 2){
			Free_tree(ptr ->R_child);
			ptr ->R_child = NULL;//防止野指针的形成
		}
	}
}
//先序遍历的递归实现
void Pre_Order_BinTree(Btree_Node* ptr){
	if(ptr){
		printf("%c  ",ptr ->data);
		Pre_Order_BinTree(ptr ->L_child);
		Pre_Order_BinTree(ptr ->R_child);
	}
}
//中序遍历的递归实现
void Mid_Order_BinTree(Btree_Node* ptr){
	if(ptr){
		Mid_Order_BinTree(ptr ->L_child);
		printf("%c  ",ptr ->data);
		Mid_Order_BinTree(ptr ->R_child);
	}
}
 //后序遍历的递归实现
void Post_Order_BinTree(Btree_Node* ptr){
	if(ptr){
		Post_Order_BinTree(ptr ->L_child);
		Post_Order_BinTree(ptr ->R_child);
		printf("%c  ",ptr ->data);
	}
}
//先序遍历的非递归实现
void NPre_Order_BinTree(Btree_Node* ptr){
	Btree_Node* ptr1 = ptr;//用于迭代的变量
	StackNode* stack = StackInit();//创建一个栈
	while(1){
		if(ptr1){//当前节点不为空
			printf("%c  ",ptr1 ->data);
			if(ptr1 ->R_child){//右孩子存在
				StackPush(&stack,ptr1 ->R_child);//右孩子入栈
			}
			ptr1 = ptr1 ->L_child;
		}else{
			if(is_StackEmpty(stack)){//当ptr1为空 栈也为空时遍历结束。 跳出循环
				break;
			}else{
				ptr1 = StackTop(stack);
				StackPop(&stack);
			}
		}
	}
}
//中序遍历的非递归实现
void NMid_Order_BinTree(Btree_Node* ptr){
	Btree_Node* ptr1 = ptr;//用于迭代的变量
	StackNode* stack = StackInit();//创建一个栈
	while(1){
		if(ptr1){//当前节点不为空
			StackPush(&stack,ptr1);
			ptr1 = ptr1 ->L_child;
		}else{
			if(is_StackEmpty(stack)){//当ptr1为空 栈也为空时遍历结束。 跳出循环
				break;
			}else{
				ptr1 = StackTop(stack);
				StackPop(&stack);
				printf("%c  ",ptr1 ->data);
				ptr1 = ptr1 ->R_child;
			}
		}
	}
}
 //后序遍历的非递归实现
void NPost_Order_BinTree(Btree_Node* ptr){
	StackNode* stack = StackInit();//创建一个栈
	Btree_Node* before_ptr = NULL;
	while(1){
		if((ptr ->L_child == before_ptr && ptr ->R_child == NULL) || 
		   (ptr ->R_child == before_ptr && before_ptr != NULL) || 
		   ( ptr ->L_child == ptr ->R_child && ptr ->L_child == NULL)){
			//遍历自己的几种情况：
			//(1)左右孩子为空既(ptr->L_child==ptr->R_child && ptr->L_child==NULL)
			//(2)左右孩子都不为空，并且左右孩子都已经遍历 既(ptr ->R_child == before_ptr && before_ptr != NULL)
			//(3)左孩子为空右孩子不为空，且右孩子已经遍历 既（与2相同）
			//(4)左孩子不为空右孩子为空，且左孩子已经遍历 既((ptr ->L_child == before_ptr && ptr ->R_child == NULL))
			printf("%c  ",ptr ->data);
			before_ptr = ptr;
			if(is_StackEmpty(stack)){//截止条件
				break;
			}else{
				ptr = StackTop(stack);
				StackPop(&stack);
			}
		}else{//左右孩子至少有一个存在且没有遍历
			StackPush(&stack,ptr);//自己入栈
			if(ptr ->L_child){//左孩存在
				if(ptr ->R_child){//右孩子存在
					StackPush(&stack,ptr ->R_child);//右孩子入栈
				}
				ptr = ptr ->L_child;
			}else{
				ptr = ptr ->R_child;
			}
		}
	}
}

void Level_Order_BinTree(Btree_Node* ptr){//层次遍历的实现
	Queue* Qptr = QueueInit();//建立一个空队列
	if(ptr){
		QueuePush(Qptr,ptr);
		while(!is_QueueEmpty(Qptr)){
			ptr = QueueFront(Qptr);
			QueuePop(Qptr);
			printf("%c  ",ptr ->data);
			if(ptr ->L_child){
				QueuePush(Qptr,ptr ->L_child);	
			}
			if(ptr ->R_child){
				QueuePush(Qptr,ptr ->R_child);	
			}
		}
	}
	QueueDestroy(Qptr);
}