关于二叉树的遍历

首先要几下：不管哪种遍历方法，左子节点先于右子节点输出。

                                **“先左后右”**

先序遍历：(PreOrderTraverse)也叫作先根遍历，前序遍历。
根—-左——-右

中序遍历：（InOrderTraverse)
左—-根——–右

后序遍历：（PostOrderTraverse)
左—–右——–根

以下图为例子：

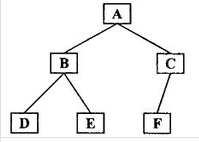
先序输出：A B D E C F
中序输出：D B E A F C
后序输出：D E B F C A

遍历可以由两种方式进行输出：递归调用和非递归调用。

递归方式调用起来比较简单，但要求逻辑想很强。
非递归调用，逻辑清晰，但是书写复杂。尤其是要用到栈来保存先前走过的路径，以便可以在访问完子树后，可以利用栈中的信息，回退到当前节点的双亲节点，进行下一步操作。

后序遍历最复杂，原因在于，后序遍历是先访问左右子树，然后访问根节点，而在非递归算法中，利用栈回退到时，并不知道是从左子树回到根节点，还是从右子树回退到根节点，如果从左子树回退到根节点，此时就应该去访问右子树，而如果从右子树回退到根节点，此时就应该访问根节点。

非递归 二叉树遍历算法实现：

#include <iostream>
using namespace std;


typedef struct node{
    char data;
    struct node *lchild;
    struct node *rchild;

}BiNode,*BiTree;


typedef struct node1
{
    //默认30个元素，这里需要一个辅助堆栈
    BiTree data[30]; 
    int top;
}Stack;

//先序递归创建树，这里注意参数的类型，T的类型是*&，如果是
//**修改代码即可
void createTree(BiTree &T) 
{
    char ch;
     cin.get(ch).get(); //过滤输入流中每次回车产生的回车符
     //这里首先判断是不是空格，如果是，则为该节点赋值NULL
     if(ch == ' ') 
     {
         T = NULL;
     }
     else
     {
        T = (BiTree)malloc(sizeof(BiNode));
        T->data = ch;
        createTree(T->lchild);
        createTree(T->rchild);

     }
}

void initstack(Stack *&st)
{
    st = (Stack *)malloc(sizeof(Stack));
    st->top = -1;
}

bool isempty(Stack *st)
{
    return st->top == -1;
}


bool isfull(Stack *st)
{
    return st->top == 16;
}

void push(Stack *st,BiTree T)
{
    //栈顶指针始终指向堆栈最上面可用的一个元素，因此入栈时候，
    //先要将指针加1，然后再执行入栈操作！
    if(!isfull(st))
        st->data[++st->top] = T;
    else
        cout << "栈已满！" <<endl;
}

BiTree pop(Stack *st)
{
    //出栈时，先取出栈顶指针指向的元素，然后再将指针减1，
    //使其指向栈中下一个可用的元素！
    if(!isempty(st))
        return st->data[st->top--];
}

BiTree gettop(Stack *st)
{
    if(!isempty(st))
        return st->data[st->top];//获取栈顶指针指向的元素

}


void preOrderNodeTraverse(BiTree T)
{
    Stack *st;
    initstack(st);
    BiTree p;
    p = T;
    while   (p!=NULL || !isempty(st))
    {
        while(p!=NULL)
        {
            cout << p->data << " ";
            push(st,p);
            p = p->lchild;
        }
        if(!isempty(st))
        {
            p = pop(st);
            p = p->rchild;
        }
    }
}

void inOrderNodeTraverse(BiTree T)
{
    Stack *st;
    initstack(st);
    BiTree p;
    p = T;
    while(p!=NULL || !isempty(st))
    {
        while(p!=NULL)
        {
            push(st,p);
            p = p->lchild;

        }
        if(!isempty(st))
        {
            p = pop(st);
            cout << p->data << " ";         
            p = p->rchild;
        }
    }

}


void postOrderNodeTraverse(BiTree T) //后序遍历
{
    BiTree p;
    Stack *st;
    initstack(st);
    p = T;
    int Tag[20]; //栈，用于标识从左（0）或右（1）返回
    while(p!= NULL || !isempty(st))
    {
        while(p != NULL)
        {
            push(st,p);
            p = p->lchild;
        }
        while(!isempty(st) && Tag[st->top] == 1)
        {
            p = pop(st);
            cout<<p->data << " ";
        }
        if(!isempty(st))
        {
            Tag[st->top] = 1;//设置标记右子树已经访问
            p = gettop(st);
            p = p->rchild;

        }
        else
            break;
    }

}

int main()
{
    cout << "Enter char one by one             Hello C++ !" <<endl;

    BiNode *T;
    createTree(T);
    cout << endl;


    cout << "PreOderNode : " ;
    preOrderNodeTraverse(T);
    cout << endl;


    cout << "InOderNode : " ;
    inOrderNodeTraverse(T);
    cout << endl;


}

最后

以上就是乐观心情为你收集整理的关于二叉树的遍历的全部内容，希望文章能够帮你解决关于二叉树的遍历所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。